Экономико-математические методы анализа хозяйственной деятельности организации

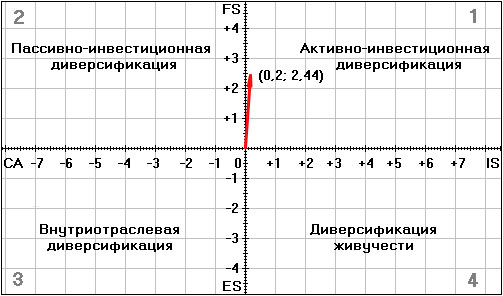
Специалисты, используя данные анализа, считают, что при стабилизации инфляции у строительной организации на последующий период есть реальные предпосылки для увеличения значения некоторых факторов. При увеличении спроса на строительную продукцию с учетом первого сценария есть возможность увеличить значения таких факторов группы "Финансовые возможности", как доля собственного капитала в общих источниках покрытия имущества, а также увеличить степень покрытия текущей деятельности за счет собственных оборотных средств. Соответственно, внедрение мероприятий по совершенствованию технологического процесса позволяет по группе "Конкурентные преимущества (СА)" повысить качество продукции, уровень использования потенциала, что, соответственно, приведет к увеличению уровня лояльности потребителей. По группе "Стабильность окружения (ES)" возможно снижение темпов инфляции, увеличение стабильности спроса с ростом платежеспособности основных потребителей. По группе "Отраслевые возможности (IS)" можно повысить уровень использования производственных ресурсов, производительности труда, что приведет к росту отдачи от средств, вложенных в капитал организации. Изменение значений некоторых факторов соответственно приводит и к изменению координат вектора стратегического направления диверсификации. При выполнении этих условий (второй сценарий) результаты расчетов вектора стратегического направления диверсификации будут соответствовать:

X = W(IS) + [-W(CA)] = 6,37 - 5,64 = 0,73;

Y= W(FS) + [-W(ES)] = 7,36 - 4,35 = 3,01.

Рис. 2.1. Вектор стратегического направления диверсификации

Метод оценки деятельности предприятия с учетом рыночной конкуренции

Оценка сравнения с эталоном

В условиях рынка предприятия стремятся к получению максимального эффекта от своей деятельности, стремятся по всем показателям деятельности превосходить своих основных конкурентов. При этом, как правило, сопоставляют результаты своей деятельности с некоторым эталонным предприятием. Для оценки деятельности может быть использован следующий алгоритм, реализацию которого рассмотрим на данных табл. 2.26:

1. задается совокупность частных критериев Р = (P_i, i = 1, N) и совокупность сравниваемых организаций O = ( O_j, j = 1, M) (Если имеются нормативные, эталонные значения таких критериев, то их необходимо учитывать в расчетах.);
2. исходные данные заносятся в таблицу, в которой в строках записаны частные критерии, а в столбцах - номера организаций;
3. в клетки таблицы заносятся значения частных критериев. В последний столбец таблицы заносится максимальное значение по каждому показателю (или эталонное значение);

4. на основе данных таблицы рассчитываются соотношения между значениями по каждому частному показателю и максимальному значению (эталону), определяются стандартизированные показатели:

   Срij = Pij : Pimax

   где Pij - значение частного критерия Рi по организации j.

   Таблица 2.26. Значения частных критериев для оценки конкуренции

   Критерий организации	"1"	"2"	"3"	Максимальное значение, Pmax
   P1	400	500	600	600
   P2	500	800	400	800
   P3	1200	900	1100	1200
   P4	700	600	800	800

   Расчеты сводятся в табл. 2.27.

   Таблица 2.27. Стандартизированные значения частных критериев

   	"1"	"2"	"3"
   P1	400 : 600 = 0,6667	500 : 600 = 0,8333	600 : 600 = 1
   P2	500 : 800 = 0,625	800 : 800 = 1	400 : 800 = 0,5
   P3	1200 : 1200 = 1	900 : 1200 = 0,75	1100 : 1200 = 0,9167
   P4	700 : 800 = 0,875	600 : 800 = 0,75	800 : 800 = 1

5. для каждой организации рассчитывают значение рейтинговой оценки по формуле:

   Rj = [(1 - C1j)² + (1 - C2j)² + (1 - C3j)² + (1 - C4j)²]^{1 / 2}.

   Значения рейтинговой оценки для организаций:

   R1 = [(1 - 0,6667)² + (1 - 0,625)² + (1 - 1)² + (1 - 0,875)²]^{1 / 2} =

   = [0,1111 + 0,1406 + 0 + 0,0156]^{1 / 2} = 0,5170;

   R2 = [(1 - 0,8333)² + (1 - 1)² + (1 - 0,75)² + (1 - 0,75)²]^{1 / 2} =

   = [0,0278 + 0 + 0,0156 + 0,0156]^1/2 = 0,242899;

   R3 = [(1 - 1)² + (1 - 0,5)² + (1 - 0,9167)² + (1 - 1)²]^{1 / 2} = [0 + 0,25 + 0, 0833 + 0]^{1 / 2} = 0,5773;

6. номера организаций располагаются в порядке убывания рейтинговой оценки:

   "3" - 0,5773; "1" - 0,5170; "2" - 0,2429.

Деятельность организации, рейтинговая оценка которой имеет минимальное значение, является наиболее эффективной.

Вданном примере наивысший рейтинг у организации "2". Следовательно, деятельность организации является наиболее эффективной.

Оценка с помощью системы бенчмаркинга

Одним из эффективных инструментов анализа и управления готовностью предприятий является система бенчмаркинга. Использование данной системы позволяет проводить мониторинг конкурентоспособности, оценивать уровень эффективности деятельности предприятия, определять отклонение уровня от заданного эталонного (оптимального) уровня, выявить достоинства и недостатки определенных аспектов управления деятельностью предприятия.

Для применения данного метода необходимо выполнить следующую последовательность действий:

1. задать множество объектов - предприятий конкурентов, подлежащих оценке П = (Пп), п = 1, Кп, где Кп - максимальное количество предприятий, участвующих в процессе анализа;

2. задать совокупность факторов, характеризующих наиболее полно качество деятельности предприятия:

   Р = (Рк), к = 1, Кф,

   где Кф - количество факторов, используемых при анализе;

3. совокупность факторов разбить на три подмножества:

   • Р - подмножество факторов, благоприятно влияющих на уровень управления:

   Р1 = (Р1z), z = 1, Z,

   где Z - количество факторов, входящих в первое подмножество;

   • Р - подмножество факторов, отрицательно влияющих на уровень управления:

   Р2 = (P2l), l = 1, L,

   где L - количество факторов, входящих во вторую группу;

   • Р - подмножество факторов, которые являются нейтральными:

   P3 = (P3m); m = 1, M,

   где М - количество факторов, входящих в третью группу.

   Z + L + M = K;

4. сформировать "предприятие-эталон", значения факторов Р должны соответствовать нормативным значениям:

   Р0 = (Р0n), n = 1, Kn;

5. задать значения показателей, характеризующих состояние предприятий-конкурентов:

   РП = {Pkj},

   где Pkj - значение j-го фактора k-го предприятия;

6. определить нормированные значения для показателей подмножеств, для этого необходимо:

   • для каждого фактора подмножества Р1 определить максимальное значение из совокупности значений:

     Хzo = max{Pzj}, z = 1, Z;

   • для каждого фактора подмножества Р2 определить минимальное значение из совокупности значений:

     Xlo = min{Plj}, l = 1, L;

   • для каждого нейтрального фактора определить среднее значение из совокупности возможных:

     Xmo = net{Pmj}, m = 1, M;
   • стандартизировать значения показателей, характеризующих предприятия, подлежащие анализу:

   • стандартные значения показателей деятельности предприятий, относящихся к подмножеству Р1 определяются по формуле:

     PCzj = Pzj : Xzo, z = 1, Z;

   • стандартные значения показателей деятельности предприятий, относящихся к подмножеству Р2 определяются по формуле:

     PClj = Xlo : Pzj, l = 1, L;

   • стандартные значения показателей деятельности предприятий, относящихся к подмножеству Р3, определяются по формуле:

     PCmj = Pzj : Xmo, m = 1, M, если PCmj ≤ Xmo;

     PCmj = Xmo : Pzj, m = 1, M, если PCmj ≥ Xmo;

7. расчет интегрального показателя оценки предприятия-конкурента:

   R = 1 : Kф * [У (Wz * PCzj) + У(Wl * PClj) + У(Wm * PCmj)],

   где Wz, Wl, Wm - весовые коэффициенты, характеризующие значимость показателя соответствующей группы.

Чем ближе значение интегрального показателя к эталону, тем эффективнее деятельность организации.

Примеры решения задач

Пример 1.

Рассчитайте фактор текущей стоимости обычного аннуитета, возникающего 7 раз, ставка дисконта ¾ 14%:

1) 2; 2) 4,29; 3) 1,85.

Правильный ответ: 2.

Решение:

А_п = [1 - 1 : (1 + R)ⁿ] : R = [1 - 1 : (1 + 0,14)⁷] : 0,14 = 4,29.

Пример 2.

Рассчитайте фактор текущей стоимости аннуитета, возникающего в течение 5 лет в конце каждого года, ставка дисконта ¾ 10%:

1) 7,72; 2) 2; 3) 3,79.

Правильный ответ: 3.

Решение:

А_п = [1- 1 : (1 + R)ⁿ] : R = [1 - 1 : (1 + 0,10)⁵] : 0,10 =3,79.

Пример 3.

Рассчитайте фактор текущей стоимости аннуитета, возникающего в течение 5 лет в начале каждого года, ставка дисконта ¾ 10%:

1) 7,72; 2) 2; 3) 3,79.

Правильный ответ: 1.

Решение:

А_ба = [(1 + R)^{n + 1} - 1] : R = [(1 + 0,10)^{5 + 1} - 1] : 0,10 =7,72.

Пример 4.

Рассчитайте фактор текущей стоимости авансового аннуитета, возникающего 15 раз, ставка дисконта ¾ 9%:

1) 24; 2) 33; 3) 14.

Решение:

А_ба = [(1 + R)^{n + 1} - 1] : R = [(1 + 0,09)^{15 + 1} - 1] : 0,09 = 33,00.

Правильный ответ: 2.

Пример 5.

Определите размер ежегодных равновеликих выплат по погашению кредита, размер которого 750 тыс. руб. взят на 3 года под 22% годовых:

1) 165 тыс. руб.; 2) 367 тыс. руб.; 3) 250 тыс. руб.

Правильный ответ: 2.

Решение:

1. Рассчитаем величину фактора взноса на погашение кредита, учитывая, что срок кредита ¾ 3 года, годовая процентная ставка ¾ 22%:

   Акр = R : [1 - 1 : (1 + R)ⁿ] = 0,22 : [1 - 1 : 1,22³] = 0,4897.

2. Определим ежегодные выплаты, если размер их должен быть один и тот же:

   РМТ =PVA * А_kp = 750 * 0,4897 =367 (тыс. руб.).

Таким образом, организации, чтобы погасить своевременно взятый кредит и плату за него, необходимо ежегодно выплачивать 367 тыс. руб. Общие выплаты организации составят: 367 * 3 = 1101 (тыс. руб.). Дополнительно выплаченные деньги организацией в размере 351 тыс. руб. (1101 - 750) представляет собой плату за использование заемного капитала.

Пример 6.

Определите ежемесячные выплаты по кредиту в размере 360 тыс. руб., выданному на 5 лет под 19% годовых:

1) 9 тыс. руб.; 2) 6 тыс. руб.; 3) 5,7 тыс. руб.

Правильный ответ: 1.

Решение:

1. Рассчитаем величину фактора взноса на погашение первого кредита, учитывая, что срок кредита 5 года, годовая процентная ставка ¾ 19%. Количество выплат, учитывая, что кредит должен погашаться каждый месяц, составит 60 (5 * 12), процентная ставка кредита за месяц ¾ 1,58%:

   А_кр = Rm : [1 - 1 : (1 + Rm)ⁿ] = 0,0158 : [1 - 1 : 1,0158⁶⁰] = 0,02591855.

2. Определим размер выплат по кредиту каждый месяц, если размер их должен быть один и тот же:

   РМТ = PVA * А_kp = 360 * 0,02592 =9 (тыс. руб.).

Следовательно, каждый месяц по кредиту следует выплачивать 9 тыс. руб. Размер основного долга за месяц составляет 6 тыс. руб. (360 : 60), плата за использование заемных средств в каждое полугодие составит 437 (тыс. руб.).

Пример 7.

Какую сумму денежных средств необходимо откладывать в конце каждого месяца на протяжении 4 лет в банк, который начисляет 11% годовых на пополняемый вклад, чтобы купить квартиру за 1200 тыс. руб.:

1) 25 тыс. руб.; 2) 20 тыс. руб.; 3) 33 тыс. руб.

Правильный ответ: 2.

Решение:

1. Определим значение фактора обычного фонда накопления (возмещения), учитывая, что период накопления необходимой суммы ¾ 4 года, а вложения должны осуществляться ежемесячно. Количество единичных периодов ¾ 4 * 12 =48 (месяцев), процентная ставка в месяц составит 0,92% (11% : 12):

   А_фно = Rm : [(1 + Rm)ⁿ - 1] = 0,0092 : [(1 + 0,0092)⁴⁸ - 1] = 0,01666495.

2. Определим величину периодически депонируемой суммы:

   РМТФ = FV * Rm : [(1 + Rm)ⁿ - 1] = 1200 * 0,016665 = 20 (тыс. руб.).

Таким образом, необходимо в конце каждого месяца депонировать по 20 тыс. руб., чтобы за 4 года накопить требуемую сумму ¾ 1200 тыс. руб. для покупки квартиры. Сумма депозитов с нарастанием составит 960 тыс. руб. (20 * 48). Разность между требуемой суммой и суммой депозитов в размере 240 тыс. руб. представляет величину процентов, начисленных на возрастающую сумму вклада по формуле сложных процентов.

Пример 8.

Какую сумму денежных средств необходимо откладывать в конце каждого квартала на протяжении 5 лет в банк, который начисляет 10% годовых на пополняемый вклад, чтобы купить квартиру за 2700 тыс. руб.:

1) 106 тыс. руб.; 2) 135 тыс. руб. 3) 68 тыс. руб.

Правильный ответ: 1.

Решение:

1. Определим значение фактора обычного фонда накопления (возмещения), учитывая, что период накопления необходимой суммы ¾ 5 лет, а вложения должны осуществляться ежеквартально. Количество единичных периодов ¾ 5 * 4 =20 (кварталов), процентная ставка в квартал составит 2,5% (10% : 4):

   А_фно = Rm : [(1 + Rm)ⁿ - 1] = 0,025 : [(1 + 0,025)²⁰ - 1] = 0,039147.

2. Определим величину периодически депонируемой суммы:

   РМТФ = FV * Rm : [(1 + Rm)ⁿ - 1] = 2700 * 0,039147 =106 (тыс. руб.).

Таким образом, необходимо в конце каждого квартала депонировать по 106 тыс. руб., чтобы за 5 лет накопить требуемую сумму ¾ 2700 тыс. руб. для покупки квартиры. Сумма депозитов с нарастанием составит 2120 тыс. руб. (20 * 106). Разность между требуемой суммой и суммой депозитов в размере 580 тыс. руб. (2700 - 2120) представляет величину процентов, начисленных на возрастающую сумму вклада по формуле сложных процентов.

Пример 9.

Какую сумму денежных средств необходимо откладывать в конце каждого года на пополняемый вклад в течение 3 лет в банк, который начисляет 12% годовых для покупки оборудования стоимостью 4,5 млн. руб.:

1) 1,33 млн. руб.; 2) 1,15 млн. руб.; 3) 1,62 млн. руб.

Правильный ответ: 1

Решение:

1. Определим значение фактора обычного фонда накопления (возмещения), учитывая, что период накопления необходимой суммы ¾ 3 года, а вложения должны осуществляться раз в год. Количество единичных периодов ¾ 3 года, процентная ставка в год ¾ 12%:

   А_фно = R : [(1 + R)ⁿ - 1] =0,12 : [(1 + 0,12)³ - 1] = 0,2963.

2. Определим величину периодически депонируемой суммы:

   РМТФ =FV * R : [(1 + R)ⁿ - 1] = 4,5 * 0,2963 = 1,3334 (млн. руб.).

Таким образом, необходимо в конце каждого года депонировать по 133,34 тыс. руб., чтобы за 3 года накопить требуемую сумму 4,5 млн. руб. для приобретения оборудования. Сумма депозитов с нарастанием составит 4,0002 млн. руб. (3 * 1,3334). Разность между требуемой суммой и суммой депозитов в размере 0,4998 млн. руб. представляет величину процентов, начисленных на возрастающую сумму вклада по формуле сложных процентов.