Эволюционные уравнения в частных производных
Сейчас мы рассмотрим нелинейное уравнения переноса
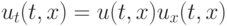
![\begin{verbatim}
class TUU : TRungeKutta
{
double h;
public TUU(int N)
: base(N)
{
h = 2.0 * Math.PI / N;
}
public double GetY(double x)
{
double res = 0;
int i;
double di;
for (i = 1; i < (N - 1) / 2; i++)
{
di = (double)i;
res += Math.Sin(di * x) * Y[i - 1];
res += Math.Cos(di * x) * Y[N - i];
}
res += Y[(N - 1) / 2];
return res;
}
\end{verbatim}](/sites/default/files/tex_cache/26c83c39faa5da016f65edadef298e51.png)
![\begin{verbatim}
public override void F(double t, double[] Y, ref double[] FY)
{
double[] DU = new double[N];
Diff(Y, ref DU);
Mult(Y, DU, ref FY);
}
int kSin(int k)
{
return k - 1;
}
int kCos(int k)
{
return N - k;
}
\end{verbatim}](/sites/default/files/tex_cache/523b35c6fcf0852f8fbe4164e9584c4f.png)
![\begin{verbatim}
void Mult(double[] U, double[] DU, ref double[] UDU)
{
int i;
for (i = 0; i < N; i++)
{
UDU[i] = 0;
}
int N2 = (N - 1)/2;
int k, m;
for (k = 1; k < (N - 1) / 2; k++)
{
for (m = 1; m < (N - 1) / 2; m++)
{
// sin kx * sin mx
if (k != m)
{
UDU[kCos(Math.Abs(k - m))] +=
0.5 * U[kSin(k)] * DU[kSin(m)];
}
if (k + m < N2)
{
UDU[kCos(k + m)] +=
-0.5 * U[kSin(k)] * DU[kSin(m)];
}
\end{verbatim}](/sites/default/files/tex_cache/fe550fca7f46ca9432068476e73c9c2f.png)
![\begin{verbatim}
// sin kx * cos mx
if (k + m < N2)
{
UDU[kSin(k + m)] +=
0.5 * U[kSin(k)] * DU[kCos(m)];
}
if (k > m)
{
UDU[kSin(k - m)] +=
0.5 * U[kSin(k)] * DU[kCos(m)];
}
if (k < m)
{
UDU[kSin(m - k)] +=
-0.5 * U[kSin(k)] * DU[kCos(m)];
}
\end{verbatim}](/sites/default/files/tex_cache/538fba421e358c8f734f2c99d59c3e29.png)
![\begin{verbatim}
// cos kx * sin km
if (k + m < N2)
{
UDU[kSin(k + m)] +=
0.5 * U[kCos(k)] * DU[kSin(m)];
}
if (m > k)
{
UDU[kSin(m - k)] +=
0.5 * U[kCos(k)] * DU[kSin(m)];
}
if (m < k)
{
UDU[kSin(k - m)] +=
-0.5 * U[kCos(k)] * DU[kSin(m)];
}
// cos kx * cos mx
if (k + m < N2)
{
UDU[kCos(k + m)] +=
0.5 * U[kCos(k)] * DU[kSin(m)];
}
if (k != m)
{
UDU[kCos(Math.Abs(k - m))] +=
0.5 * U[kCos(k)] * DU[kSin(m)];
}
}
}
}
\end{verbatim}](/sites/default/files/tex_cache/d50171e70a93badd2bbb9b7e9534880d.png)
![\begin{verbatim}
void Diff(double[] Y, ref double[] DY)
{
int i;
double di;
for (i = 1; i < (N - 1) / 2; i++)
{
di = (double)i;
DY[i - 1] = -di * Y[N - i];
DY[N - i] = di * Y[i - 1];
}
DY[(N - 1) / 2] = 0;
}
}
\end{verbatim}](/sites/default/files/tex_cache/35fe0245208b8cae206680b04d1941e5.png)
![\begin{verbatim}
int N = 257;
double h = 0.001;
double[] Y0 = new double[N];
TUU UU = new TUU(N);
for (i = 0; i < N; i++)
{
Y0[i] = 0;
}
Y0[1] = 1;
UU.SetInit(0, Y0);
t = 0;
while (UU.GetCurrent() < (0.3 + h / 2.0))
{
t = UU.GetCurrent();
UU.NextStep(h);
}
Fout = File.CreateText("uu.txt");
for (i = 0; i < N; i++)
{
x = (double)i * (2.0 * Math.PI) / (double)N;
Fout.WriteLine("{0}\t{1}", x, UU.GetY(x));
}
Fout.Close();
\end{verbatim}](/sites/default/files/tex_cache/17716032d9f3f9d0e3859df961054c45.png)
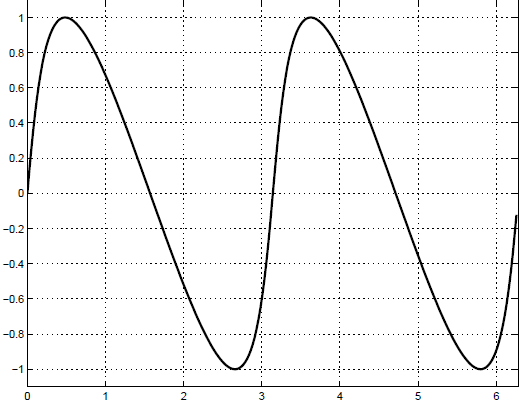
На графике 17.4 мы приведем график приближенного решения при 
. К сожалению мы не имеем точного решения нелинейного
уравнения, поэтому мы не приводим графика погрешности
приближенного решения. Видно, что волна "пытается" обрушится.
Ключевые термины
Распределенные системы - бесконечно мерные системы дифференциальных уравнений.
Начальное условие - функция, которой равно решение в начальный момент.
Абстрактная задача Коши - дифференциальное уравнение для функций со значениями в банаховом пространстве с заданным начальным условием.
Проекционный метод - метод аппроксимации эволюционных уравнений в частных производных системами обыкновенных дифференциальных уравнений.
Аналитико-числовые методы - численные методы которые содержат операции, выполняемые с использованием аналитического представления математических объектов.
Краткие итоги: Рассмотрены проекционные методы решения эволюционных уравнений в частных производных. Показано, что использование аналитико-числовых методов позволяет существенно улучшить точность расчетов.