Объектно-ориентированная реализация действительных чисел
Цель лекции: Дать объектно-ориентированную трактовку конструктивных действительных чисел. Показать важность данного понятия для конструирования вычислительных процедур.
Основным понятием вычислительной математики и математики вообще
является понятие числа. Способность к счету является
фундаментальным свойством человека. Проблема, впрочем, состоит в
том, что большинство разделов математики оперирует понятием
действительного числа. Однако мы исходим из того, что механически
можно выполнять лишь операции с целыми числами  . Под
операциями мы понимаем операцию сложения, умножения на -1, а
также сравнения двух целых чисел. Поскольку рациональное число
представляет собой пару целых чисел (числитель/знаменатель), то
эти же операции можно считать механическими и для рациональных
чисел
. Под
операциями мы понимаем операцию сложения, умножения на -1, а
также сравнения двух целых чисел. Поскольку рациональное число
представляет собой пару целых чисел (числитель/знаменатель), то
эти же операции можно считать механическими и для рациональных
чисел  . Драма человечества состояла в открытии
несоизмеримости некоторых величин. С этого момента нам
потребовались числа, которые не являются механически обозримыми. С
древности были известны некоторые иррациональные числа, такие как
. Драма человечества состояла в открытии
несоизмеримости некоторых величин. С этого момента нам
потребовались числа, которые не являются механически обозримыми. С
древности были известны некоторые иррациональные числа, такие как  . Полноценная теория действительных чисел
требует применения методов математического анализа. Наиболее ясное
построение действительных чисел основано на пополнении
метрического пространства рациональных чисел. Идея этого
пополнения состоит в том, что все фундаментальные
последовательности рациональных чисел разбиваются на классы
эквивалентности. Две фундаментальные последовательности
рациональных чисел
. Полноценная теория действительных чисел
требует применения методов математического анализа. Наиболее ясное
построение действительных чисел основано на пополнении
метрического пространства рациональных чисел. Идея этого
пополнения состоит в том, что все фундаментальные
последовательности рациональных чисел разбиваются на классы
эквивалентности. Две фундаментальные последовательности
рациональных чисел  и
и 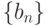 объявляются
эквивалентными если для любого
объявляются
эквивалентными если для любого 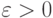 существуют такое
существуют такое 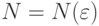 , что для всех
, что для всех  выполнено неравенство
выполнено неравенство
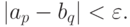
Прежде чем продолжить рассмотрение действительных чисел, введем
формально важнейшее понятие - понятие алгоритма. Интуитивно
алгоритм понимается, как однозначное предписание элементарных
действий. Согласно тезису Черча-Тьюринга любая интуитивно
вычислимая функция может быть вычислена с помощью машины Тьюринга.
Есть и другие эквивалентные формальные определения алгоритма на
основе нормальных алгорифмов Маркова, частично вычислимых функций,
структурных программ и др. Машина Тьюринга эквивалентна более
простой  .
.
Гипотетическая машина Поста состоит из бесконечной ленты, разбитой
на отельные ячейки. Каждая ячейка может быть помечена либо  ,
либо
,
либо  . Также у машины Поста есть воображаемая каретка, которая
в каждый момент может находиться только над одной из ячеек.
Каретка управляется согласно программе, которая состоит из шести
команд:
. Также у машины Поста есть воображаемая каретка, которая
в каждый момент может находиться только над одной из ячеек.
Каретка управляется согласно программе, которая состоит из шести
команд:
-
 сдвиг каретки вправо
сдвиг каретки вправо -
 сдвиг каретки влево
сдвиг каретки влево -
 записать в текущую ячейку
записать в текущую ячейку 
-
 записать в текущую ячейку
записать в текущую ячейку 
-
 если в текущей ячейке записано
если в текущей ячейке записано  , то
, то 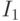 -ой строке программы, иначе к строке
-ой строке программы, иначе к строке 
-
 остановка
остановка
Работа машины Поста задается программой, содержащей конечное число
команд, и начальной конфигурацией (состояние ленты и положение
каретки). Начальная конфигурация должна содержать лишь конечное
число ячеек, содержащих  . Мы будем говорить, что функция
. Мы будем говорить, что функция 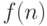 натурального аргумента и принимающая натуральное значение,
алгоритмически вычислима или просто вычислима для аргумента
натурального аргумента и принимающая натуральное значение,
алгоритмически вычислима или просто вычислима для аргумента  ,
если существует какая-нибудь машина Поста, что если начальная
конфигурация содержит ровно
,
если существует какая-нибудь машина Поста, что если начальная
конфигурация содержит ровно  ячеек, содержащих
ячеек, содержащих  , то работа
машина обязательно закончится командой
, то работа
машина обязательно закончится командой  и в момент остановки
на ленте будет ровно
и в момент остановки
на ленте будет ровно 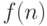 ячеек, содержащих
ячеек, содержащих  .
.
Программирование даже простейших функций на машине Поста очень громоздко и сложно, поэтому мы будем обращаться к машине Поста лишь как к формальному определению алгоритма. Заметим еще, что поскольку можно построит алгоритм (и соответственно машину Поста), которая однозначно сопоставляет каждому натуральному числу --- рациональное число, то мы будем рассматривать алгоритмически вычислимые функции и рациональных аргументов, и принимающие рациональные значения. И даже функции отображающую любое счетное множество в другое счетное множество.
Мы часто будем говорить, что последовательность рациональных
чисел 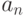 является вычислимой, если существует такая вычислимая
функция
является вычислимой, если существует такая вычислимая
функция  , что
, что

Вернемся к вещественным числам. Данное выше определение (и любое другое) вызывает ряд вопросов. В самом деле, любое вещественное число - это класс эквивалентности фундаментальных последовательностей. Во-первых, для любого ли вещественного числа можно построить вычислимую фундаментальную последовательность? Ответ, очевидно, нет! Почему? Потому что множество вещественных чисел имеет мощность континуума, а количество всех алгоритмов (машин Поста) счетно. Во-вторых, даже если у нас есть вычислимая фундаментальная последовательность, то это еще не означает, что мы можем узнать предел этой последовательности.
Введем понятие вычислимой сходимости последовательности.
Последовательность 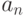 называется вычислимо сходящейся к числу
называется вычислимо сходящейся к числу  , если существует такая вычислимая функция
, если существует такая вычислимая функция  , что для любого рационального
, что для любого рационального 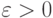 выполнено
выполнено

 .
.Число  называется конструктивным действительным
числом, если существует вычислимая последовательность
рациональных чисел, которая вычислимо сходиться к
называется конструктивным действительным
числом, если существует вычислимая последовательность
рациональных чисел, которая вычислимо сходиться к  . Можно
сказать, что конструктивное действительное число это пара
вычислимых функций
. Можно
сказать, что конструктивное действительное число это пара
вычислимых функций  . Можно конструктивное
действительное число представить в виде одной вычислимой функции:
. Можно конструктивное
действительное число представить в виде одной вычислимой функции:  , которая по заданному
, которая по заданному 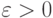 вычисляет
рациональное число такое, что:
вычисляет
рациональное число такое, что:

Реализуем абстрактный класс, который будет заготовкой для классов различных конструктивных действительных чисел.

Разумеется, на компьютере мы можем реализовать лишь некоторое
приближение к конструктивному действительному числу.
Действительно, переменная  , во-первых, не может быть
произвольным рациональным числом, а, во-вторых, не с любой
точностью мы можем проводить вычисления. И еще заметим, что
переменные типа
, во-первых, не может быть
произвольным рациональным числом, а, во-вторых, не с любой
точностью мы можем проводить вычисления. И еще заметим, что
переменные типа  представляют собой некоторое подмножество
рациональных чисел.
представляют собой некоторое подмножество
рациональных чисел.
Возникает естественный вопрос - а какие есть примеры
конструктивных действительных чисел, не являющихся рациональными?
Конструктивными действительными числами являются, например,  . Для примера реализуем первые
два из этих конструктивных чисел. Для вычисления числа
. Для примера реализуем первые
два из этих конструктивных чисел. Для вычисления числа  мы
воспользуемся рядом Лейбница:
мы
воспользуемся рядом Лейбница:

 , но мы выбрали ряд Лейбница по причине, что для
знакопеременного ряда остаток ряда оценивается через модуль
последнего слагаемого частичной суммы.
, но мы выбрали ряд Лейбница по причине, что для
знакопеременного ряда остаток ряда оценивается через модуль
последнего слагаемого частичной суммы.
Для построение конструктивного действительного числа  мы
реализуем метод дихотомии для решения уравнения
мы
реализуем метод дихотомии для решения уравнения
![x^2-2=0,\quad x\in[1,2].](/sites/default/files/tex_cache/abef3e10eb2db47bc8acbdf5c40a1e69.png)

Возникает еще один вопрос, если среди действительных чисел не конструктивные действительные числа, то значит есть (и их континуум!) неконструктивных действительных чисел. А есть ли пример такого числа? Но на бумаге невозможно описать неконструктивный объект - можно лишь доказать (неконструктивно) его существование.
Заметим, что в рамках конструктивной математики работать с конструктивными действительными числами весьма сложно. Например доказывается теорема о том, что для произвольного конструктивного действительного числа нет алгоритма, позволяющего определить равно это число нулю или нет. В частности, в рамках конструктивных действительных чисел простейшее линейное уравнение

Однако есть операции для конструктивных действительных чисел, которые являются алгоритмически разрешимыми, например сложение двух конструктивных чисел. Реализуем соответствующий класс

Ключевые термины
Вычислимая последовательность чисел - числовая последовательность, каждый элемент которой может быть получен с помощью вычислимой функции по номеру.
Конструктивное действительное число - число, являющееся вычислимым пределом вычислимой последовательности рациональных чисел.
Машина Поста - гипотетическая вычислительная машина, эквивалентная машине Тьюринга.
Тезис Черча-Тьюринга - утверждение, что любая интуитивно вычислимая функция может быть вычислена с помощью машины Тьюринга.
Краткие итоги: Введено фундаментальное понятие конструктивного действительного числа. Дано уточнение понятия алгоритма с помощью машины Поста. С помощью объектно-ориентированного подхода реализованы классы конструктивных действительных чисел.
