Oбъектно-ориентированная реализация числовых функций

Цель лекции: Научить создавать классы, для описания функций и реализации операций над функциями.

Пусть и - произвольные множества. Мы под абстрактной функцией будем понимать правило, которое элементу множества сопоставляет элемент множества . Записывается это в виде

Мы будем рассматривать только однозначные функции. В противном случае всегда можно вместо множества рассматривать подмножества множества . Функция может быть определена не на всем множестве , а только на некотором (непустом) подмножестве . Множество называется областью определения функции .

Мы будем рассматривать функции , определенные на подмножествах . Однако в качестве множества у нас могут выступать различные множества. Для этого создадим универсальный класс, который сможет представлять любые другие объекты.

Заметим, что мы воспользовались типом . Этот тип является родительским для всех объектов C#, поэтому возможно в классе хранить ссылку на любой объект (элемент множества ).

Абстрактный класс представляющий функцию, заданную на некотором отрезке , выглядит следующим образом

Для реализации заданной функции, необходимо создать класс наследник, в котором нужно переопределить метод . Для случая числовых функций, в которых множество также является , мы определим более удобный класс, наследник от . В этом классе метод возвращает тип , а не , поэтому нет необходимости в преобразовании типов.

Покажем как выглядит класс для описания функции .

Теперь покажем, как с помощью объектно-ориентированного подхода можно выполнять различные операции над функциями. Создадим класс, который будет представлять собой производную от исходного класса-функции.

Теперь с использованием наших классов мы вычислим производные от функции .

При выполнении этого кода мы получим: Что близко к точным значениями и .

Мы реализовали класс для представления функций, убедились, что наши классы в состоянии выполнять различные действия с функциями. Однако в наших вычислениях мы использовали тип для представления действительных чисел. Этот подход означает, что мы рассматриваем лишь подмножество рациональных чисел. Но из прошлой лекции мы знаем, что на компьютере можно реализовать и большее --- машина Поста (а значит теоретически и любой компьютер) может оперировать конструктивными действительными числами. Поэтому естественно рассматривать функции как отображение одного конструктивного действительного числа в другое конструктивное действительное число. В конструктивной математике есть фундаментальное понятие - конструктивная функция. Однако, как известно, единого определения конструктивной функции в строгих рамках конструктивной математики не существует.

Мы дадим определение функции Маркова. Но сначала мы должны ответить на естественный вопрос - а какие конструктивные действительные числа называются равными? Если исходить из того, что конструктивно действительное число - это пара алгоритмов, то из неравенства этих алгоритмов еще не следует неравенство конструктивных действительных чисел. Поэтому мы будем говорить, что равно и писать 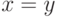, если существует такая вычислимая функция , что

для всех .

Пусть 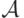- некоторое множество конструктивных действительных чисел такое, что если и - другое конструктивное действительное число и 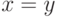, то . Конструктивной функцией или функцией Маркова называется такой алгоритм , что

1. Для любого 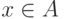определено и есть конструктивное действительное число.
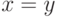2. Если и суть конструктивные действительные числа, и , то .

Ключевые термины

Абстрактная функция - однозначное отображение одно множества в другое.

Конструктивная функция - алгоритм сопоставляющий одному конструктивному действительному числу другое конструктивное действительное число.

Область определения функции - множество на, котором определена функция.

Краткие итоги: Реализован абстрактный класс на языке C#, реализующий функции. Разработаны классы, реализующие конкретные числовые функции и операции над ними.