Вычислительные эксперименты в моделировании волн-убийц
Цель лекции: Продемонстрировать возможности современных вычислительных экспериментов.
На последней лекции мы рассмотрим реальные вычислительные эксперименты, которые были проведены в Институте океанологии им. П.П. Ширшова РАН совместно с Физическим институтом им. П.Н. Лебедева РАН и Университетом Аризоны (США). Были проведены масштабные вычислительные эксперименты по моделированию волн-убийц в мировом океане.
Под волнами-убийцами в океанологии понимаются внезапные поверхностные волны экстремальной амплитуды. В последние несколько лет были получены экспериментальные данные, подтверждающие существование этого феномена. Волны-убийцы наносят серьезный ущерб морскому судоходству и морским нефтяным платформам. Особую опасность волнам-убийцам придает внезапность их возникновения и огромная энергия этих волн. Обычно амплитуда волн-убийц достает 20-30 метрового значения.
После получения натурных данных началось систематическое изучение этого эффекта. В лаборатории нелинейных волновых процессов Института океанологии им. П.П. Ширшова РАН проводились систематические вычислительные эксперименты по изучению волн-убийц. С помощью доказательных вычислений было показано, что волны-убийцы могут возникать в ходе нелинейной динамики идеальной жидкости со свободной поверхностью. Опишем последние вычислительные эксперименты.
Мы решали численно уравнения Эйлера, описывающие глубокую
идеальную жидкость со свободной поверхностью в двумерной геометрии 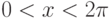 ,
, 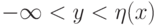 . Граничные условия на концах
интервала
. Граничные условия на концах
интервала 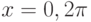 , предполагались периодическими.
, предполагались периодическими.
Течение предполагалось потенциальным, а жидкость несжимаемой,

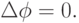
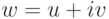 .
Отображение задается функцией
.
Отображение задается функцией 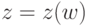 ,
,  .
.Динамические уравнения формулируются для переменных Дьяченко
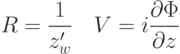
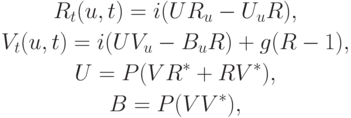 |
( 22.1) |
 - оператор проектирования на нижнюю полуплоскость
- оператор проектирования на нижнюю полуплоскость 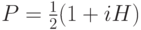 ,
,  - аналог оператора Гильберта для
периодического случая
- аналог оператора Гильберта для
периодического случая=\frac{1}{2\pi}v.p.\int_0^{2\pi}\frac{f(u')}{\tan(\frac{u'-u}{2})}du'](/sites/default/files/tex_cache/b623384924f8b1371e3f2e993d269251.png)
В наших экспериментах начальные условия определялись как ансамбль
бегущих в одну сторону волн со средним значением волнового числа 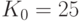 .
.
Мы предполагали, что начальное возмущение поверхности задается суммой гармоник со случайными фазами
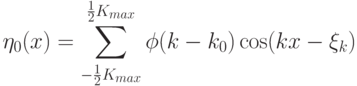 |
( 22.2) |
 - полное число спектральных мод,
- полное число спектральных мод, 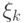 -
случайная величина, равномерно распределенная на интервале
-
случайная величина, равномерно распределенная на интервале 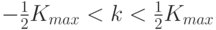 .
.Начальные значения поля скоростей предполагались связанными с 22.2 формулами линейной теории. Конформное преобразование осуществлялось при помощи итерационного алгоритма, предложенного А.И.Дьяченко.
Функция 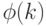 определялась по формуле
определялась по формуле
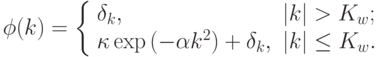 |
( 22.3) |
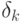 - независимые случайные параметры равномерно
распределенные на интервале
- независимые случайные параметры равномерно
распределенные на интервале 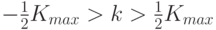 .
.Число 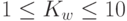 определяло спектральную ширину,
определяло спектральную ширину, 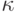 ,
,  - "внутренние" параметры спектра, определенные так,
чтобы "внешние" параметры - средняя крутизна
- "внутренние" параметры спектра, определенные так,
чтобы "внешние" параметры - средняя крутизна 
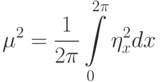

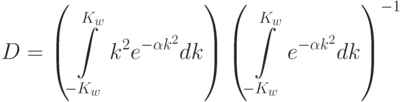
 и следили за тем, чтобы вклад в нее случайного
шума составлял не более трех процентов. Было проделано 5000
"элементарных" экспериментов. В каждом эксперименте время
менялось в интервале
и следили за тем, чтобы вклад в нее случайного
шума составлял не более трех процентов. Было проделано 5000
"элементарных" экспериментов. В каждом эксперименте время
менялось в интервале 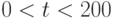 , что соответствовало приблизительно
500 периодам волн. Если происходило обрушение волн, счет
прекращался досрочно. В расчетах полное число гармоник было
, что соответствовало приблизительно
500 периодам волн. Если происходило обрушение волн, счет
прекращался досрочно. В расчетах полное число гармоник было 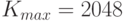 или
или 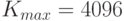 в зависимости от полной энергии,
которая менялась в пределах
в зависимости от полной энергии,
которая менялась в пределах 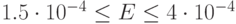 .
.Регистрация волн-убийц производилась следующим образом. После
окончания элементарного эксперимента рассчитывалась величина 

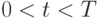 ,
,
"Волна-убийца" фиксировалась если параметр  превышал
критическое значение
превышал
критическое значение 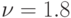 . Данное определение количественно
лишь не существенно отличается от общепринятого, когда считается,
что волны-убийцы вдвое превышают существенную высоту (significant
wave height) Требовалось также, чтобы локальная крутизна волны
. Данное определение количественно
лишь не существенно отличается от общепринятого, когда считается,
что волны-убийцы вдвое превышают существенную высоту (significant
wave height) Требовалось также, чтобы локальная крутизна волны 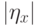 превышала критическое значение
превышала критическое значение 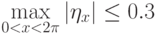 . Это требование вызвано
очевидными физическими соображениями и является весьма
существенным.
. Это требование вызвано
очевидными физическими соображениями и является весьма
существенным.
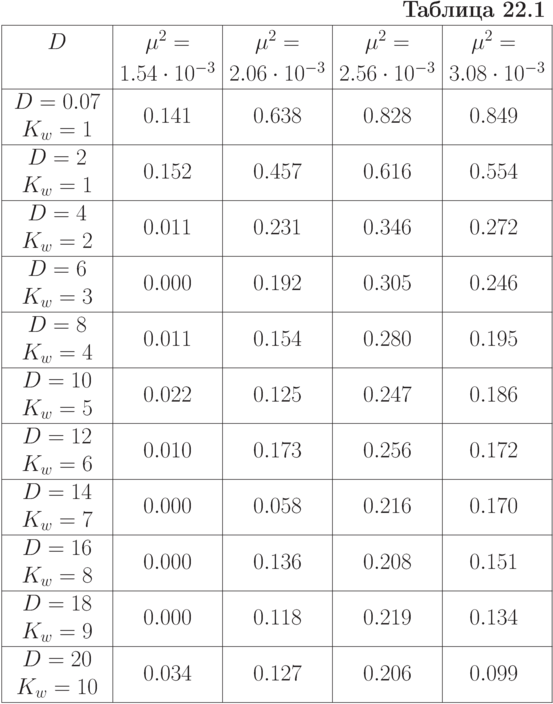
Результаты экспериментов приведены в таблице 22.1. По горизонтали
отложены значения дисперсии, по вертикальной - значения квадрат
крутизны. Число "активных" мод начального условия для каждого
эксперимента также показано. Из наших данных следует, что даже для
волн довольно умеренной крутизны ( 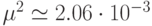 ,
,  ) образование экстремальной волны за столь
короткий отрезок времени как 500 периодов (при периоде 10 секунд
это меньше полутора часов) есть весьма вероятное событие даже,
если спектральная ширина по волновым числам сравнима с несущим
волновым числом. Собственно, этот эксперимент и подчеркивает
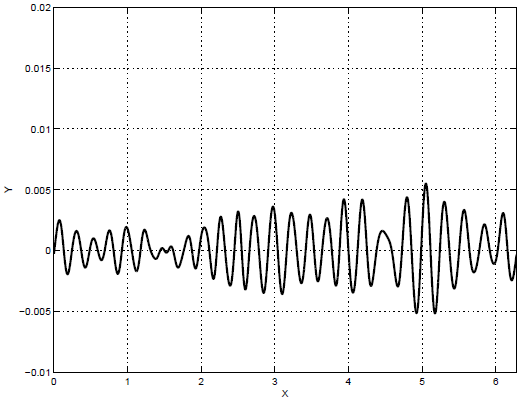
"обыденность" экстремальных волн. На рисунке 22.1 приведен
профиль начальной волны со средней крутизной -
) образование экстремальной волны за столь
короткий отрезок времени как 500 периодов (при периоде 10 секунд
это меньше полутора часов) есть весьма вероятное событие даже,
если спектральная ширина по волновым числам сравнима с несущим
волновым числом. Собственно, этот эксперимент и подчеркивает
"обыденность" экстремальных волн. На рисунке 22.1 приведен
профиль начальной волны со средней крутизной -  и дисперсией
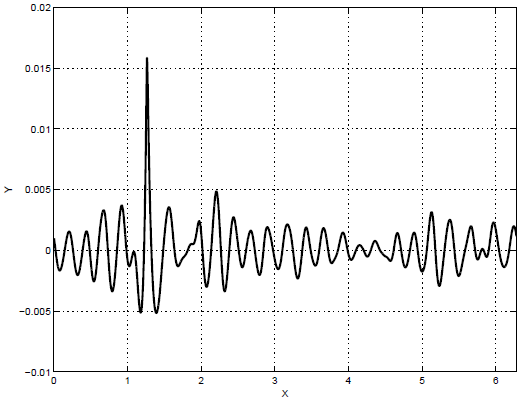
и дисперсией 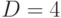 . На рисунке 22.2
показан профиль волны-убийцы для этой волны. Время образование
волны-убийцы -
. На рисунке 22.2
показан профиль волны-убийцы для этой волны. Время образование
волны-убийцы - 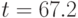 , параметр
, параметр  максимальная
крутизна -
максимальная
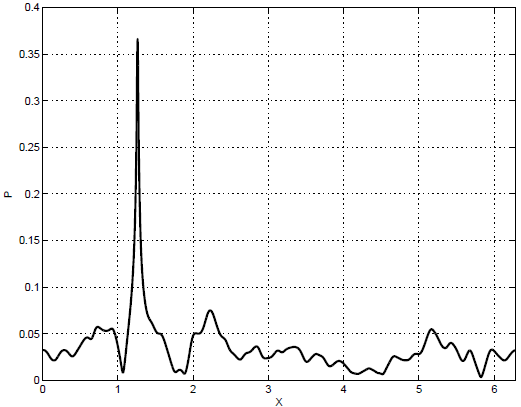
крутизна - 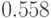 . На рисунке 22.3 приведена плотность импульса
в момент образования этой волны-убийцы.
. На рисунке 22.3 приведена плотность импульса
в момент образования этой волны-убийцы.
Интересно, что вероятность возникновения экстремальных волн,
рассматриваемая как функция от средней крутизны при заданной
дисперсии имеет максимум при весьма умеренных крутизнах
( 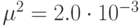 ) а затем убывает при увеличении крутизны.
Этот факт объясняется увеличением силы конкурирующего эффекта -
обрушения волн. Использованная нами схема счета позволяет вести
эксперимент только до первого обрушения. Мы полагаем, что при
использовании более совершенных методик, зависимость вероятности
возникновения экстремальных волн от крутизны остается монотонной.
) а затем убывает при увеличении крутизны.
Этот факт объясняется увеличением силы конкурирующего эффекта -
обрушения волн. Использованная нами схема счета позволяет вести
эксперимент только до первого обрушения. Мы полагаем, что при
использовании более совершенных методик, зависимость вероятности
возникновения экстремальных волн от крутизны остается монотонной.
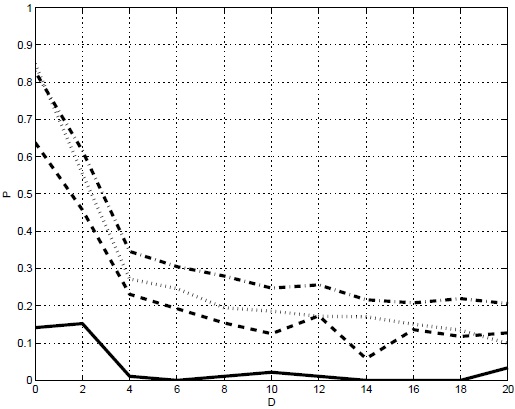
На рисунке 22.4 приведены частоты возникновения волн-убийц в
зависимости от дисперсии: 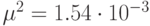 - сплошная линия,
- сплошная линия,  - "тире",
- "тире", 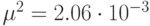 - точечная линия,
- точечная линия,  -
"точка-тире".
-
"точка-тире".
Ключевые термины
Волна-убийца - поверхностная волна экстремальной амплитуды в океане.
Уравнение Эйлера - основное уравнение, описывающее динамику идеальной жидкости.
Краткие итоги: Дано описание вычислительных экспериментов. Приведены результаты о статистических характеристик волн-убийц.