Объектно-ориентированный подход в моделировании функциональных пространств
Цель лекции: Реализовать важный инструмент современной математики - функциональные пространства. Показать их применимость для реализации вычислительных процедур.
В современной математике часто изложение построено на использовании функциональных пространств и методов функционального анализа. Среди фундаментальных понятий функционального анализа мы рассмотрим: метрические пространства, банаховы пространства и гильбертовы пространства. Мы будем предполагать, что понятие линейного пространства является известным.
Метрическим пространством называется пара 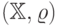 , где
, где  некоторое множество произвольной природы, а
некоторое множество произвольной природы, а  числовая
функция
числовая
функция
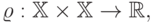
 :
: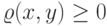
-
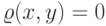 тогда и только тогда, когда
тогда и только тогда, когда 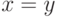
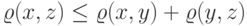
В этом случае функция  называется метрикой или
расстоянием.
называется метрикой или
расстоянием.
Метрика позволяет ввести фундаментальное понятие сходимости в
метрическом пространстве. Пусть задано метрическое пространство 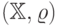 , которое мы будем обозначать
, которое мы будем обозначать  или просто
или просто  , если это не приводит к недоразумению. Последовательность
, если это не приводит к недоразумению. Последовательность 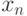 сходиться к элементу
сходиться к элементу  , если для любого
, если для любого 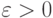 существует такое
существует такое 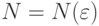 , что
, что
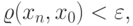
 . В этом случае пишут
. В этом случае пишут
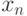 называется фундаментальной, если для
любого
называется фундаментальной, если для
любого 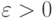 существует такое
существует такое 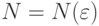 , что
, что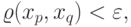
 . Если метрическое пространство такое, что любая
фундаментальная последовательность имеет предел, то такое
пространство называется полным метрическим пространством.
. Если метрическое пространство такое, что любая
фундаментальная последовательность имеет предел, то такое
пространство называется полным метрическим пространством.Приведем некоторые примеры метрических пространств.
Пространство 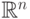 с евклидовой метрикой
с евклидовой метрикой
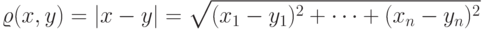
Пространство непрерывных на ![[a,b], -\infty<a<b<\infty](/sites/default/files/tex_cache/5b95b4643e606ed318c0d6274ef58fc0.png) функций
функций ![C[a,b]](/sites/default/files/tex_cache/d930e3053f32dbc51f14e870df59674d.png) является полным метрическим пространством с метрикой
является полным метрическим пространством с метрикой
![\varrho(f,g)=\max\limits_{x\in[a,b]}|f(x)-g(x)|.](/sites/default/files/tex_cache/e6832b784fb069d7fa39595e619c0f3f.png)
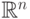 является бесконечномерным
функциональным пространством.
является бесконечномерным
функциональным пространством.Во множестве непрерывных на ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) функций можно ввести другую
метрику
функций можно ввести другую
метрику
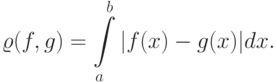
![L[a,b]](/sites/default/files/tex_cache/9af25763d5499ed302b52ba2c3aca7b6.png) .
Пространство
.
Пространство ![L[a,b]](/sites/default/files/tex_cache/9af25763d5499ed302b52ba2c3aca7b6.png) не является полным. Например
последовательность
не является полным. Например
последовательность 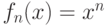 является фундаментальной на в
является фундаментальной на в ![C[0,1]](/sites/default/files/tex_cache/3db697426056e27680c2e275d81fb9cf.png) , но не имеет предела в пространстве
, но не имеет предела в пространстве ![L[0,1]](/sites/default/files/tex_cache/a1bdcff97412555e6a892bd5d65a2bbf.png) .
.Реализуем теперь абстрактное метрическое пространство на C#.
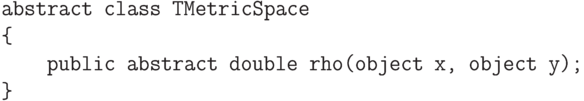
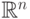 . Для этого сначала нам
потребуется создать класс, представляющий
. Для этого сначала нам
потребуется создать класс, представляющий  -мерный вектор.
-мерный вектор.![\begin{verbatim}
class TRn
{
double[] A;
int N = 0;
public TRn(int N)
{
this.N = N;
A = new double[N + 1];
}
public double this[int index]
{
get { return A[index]; }
set { A[index] = value; }
}
public int GetN()
{
return N;
}
}
\end{verbatim}](/sites/default/files/tex_cache/56821b44f534b0daa1129247cb0ac3ec.png)
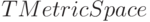 .
.![\begin{verbatim}
class TRnMetric : TMetricSpace
{
public override double rho(object x, object y)
{
TRn X, Y;
X = (TRn)x;
Y = (TRn)y;
double res = 0;
for (int i = 1; i <= X.GetN(); i++)
{
res += (X[i] - Y[i]) * (X[i] - Y[i]);
}
return Math.Sqrt(res);
}
}
\end{verbatim}](/sites/default/files/tex_cache/b6f2211bef878a8816fe4bfc1eff2eb4.png)
Проверим "в бою" наши классы. Попробуем вычислить длину диагонали единичного куба.
![\begin{verbatim}
TRn A = new TRn(3);
TRn B = new TRn(3);
A[1] = 0;
A[2] = 0;
A[3] = 0;
B[1] = 1;
B[2] = 1;
B[3] = 1;
TRnMetric M = new TRnMetric();
Console.WriteLine("R = {0}", M.rho(A, B));
\end{verbatim}](/sites/default/files/tex_cache/b2bb5a020e12180945ab701323cde177.png)
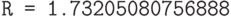
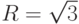 .
.Среди метрических пространств есть такие пространства, в которых
можно ввести не только расстояние между элементами, но и длину
каждого элемента. Эта длина называется нормой. Линейное
пространство  называется нормированным, если в нем
можно ввести норму для каждого элемента, обозначаемую
называется нормированным, если в нем
можно ввести норму для каждого элемента, обозначаемую 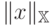 ,
удовлетворяющую следующим условиям для всех
,
удовлетворяющую следующим условиям для всех  и
и 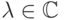
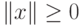
-
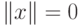 тогда и только тогда, когда
тогда и только тогда, когда 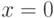


Сразу заметим, что любая норма порождает в нормированном пространстве метрику по формуле

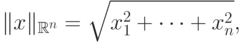
![\|f\|_{C[a,b]}=\max\limits_{x\in[a,b]}|f(x)|,](/sites/default/files/tex_cache/c8c2d9a41deca62c751f1d739abde841.png)
![\|f\|_{L[a,b]}=\left(\int\limits_a^b|f(x)|^2dx\right)^{1/2}.](/sites/default/files/tex_cache/f4a8aeb4187dc1e6eb3e9508f2de899b.png)
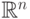 и
и ![C[a,b]](/sites/default/files/tex_cache/d930e3053f32dbc51f14e870df59674d.png) являются банаховыми
пространствами, а пространство
являются банаховыми
пространствами, а пространство ![L[a,b]](/sites/default/files/tex_cache/9af25763d5499ed302b52ba2c3aca7b6.png) только нормированным.
только нормированным.