Объектно-ориентированный подход в моделировании функциональных пространств
Посмотрим как на C# выглядят нормированные (банаховы) пространства.
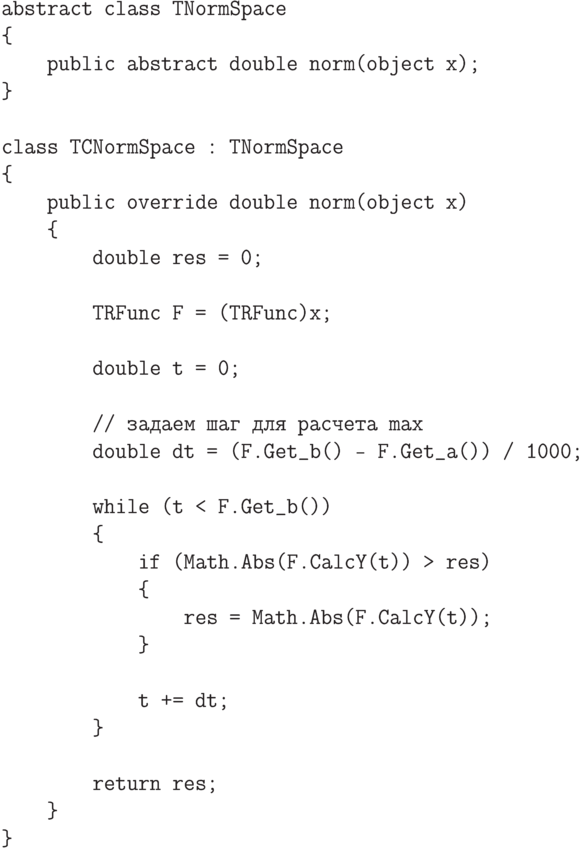
 , а потом реализуем класс-наследник для пространства
, а потом реализуем класс-наследник для пространства ![C[a,b]](/sites/default/files/tex_cache/d930e3053f32dbc51f14e870df59674d.png) . Чтобы вычислить нормы некоторых функций реализуем эти
функции.
. Чтобы вычислить нормы некоторых функций реализуем эти
функции.
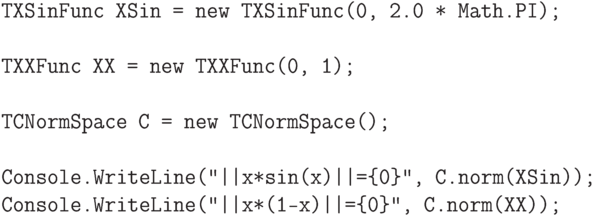
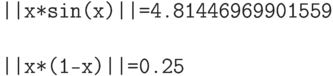
Чтобы вычислять метрику между двумя функциями в пространстве с помощью нормы реализуем еще один класс, который будет представлять разность двух числовых функций.

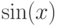 и
и  в
пространстве
в
пространстве ![C[a,b]](/sites/default/files/tex_cache/d930e3053f32dbc51f14e870df59674d.png)


 . И это при том, что норма каждой из функций равна
. И это при том, что норма каждой из функций равна  !
!Однако в некоторых функциональных пространствах можно ввести не
только расстояние между функциями, но и угол. Эти пространства
называются предгильбертовым. Линейное пространство  называется предгильбертовым, если в этом пространстве можно
ввести скалярное произведение
называется предгильбертовым, если в этом пространстве можно
ввести скалярное произведение 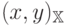 , которое должно
удовлетворять следующим условиям для любых
, которое должно
удовлетворять следующим условиям для любых  и
и 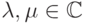
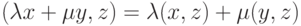

-
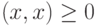 , причем
, причем 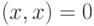 тогда и только тогда, когда
тогда и только тогда, когда 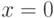
Предгильбертово пространство является также и нормированным и, соответственно, метрическим. Скалярное произведение порождает норму по формуле
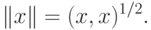
Конечномерное пространство 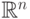 является гильбертовым со
скалярным произведением
является гильбертовым со
скалярным произведением
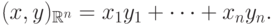
![L[a,b]](/sites/default/files/tex_cache/9af25763d5499ed302b52ba2c3aca7b6.png) также можно ввести скалярное пространство
по формуле
также можно ввести скалярное пространство
по формуле![(f,g)_{L[a,b]}=\int\limits_a^bf(x)\overline{g(x)}dx.](/sites/default/files/tex_cache/51dd44523af3ac13ec21ffc5f115d12c.png)
Для двух ненулевых элементов вещественного предгильбертова
пространства можно ввести понятие угла  . Пусть
. Пусть 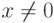 и
и 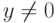 , тогда углом между этими элементами является величина
, тогда углом между этими элементами является величина
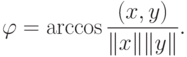
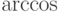 существует.
Действительно, согласно этому неравенству
существует.
Действительно, согласно этому неравенству
![L[a,b]](/sites/default/files/tex_cache/9af25763d5499ed302b52ba2c3aca7b6.png) .
.
Теперь вычислим некоторые скалярные произведения.
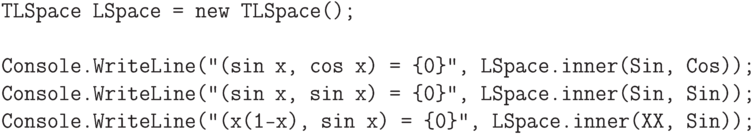
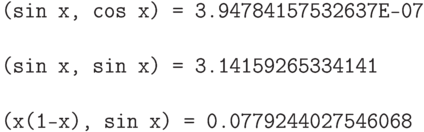
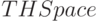 метод для подсчета угла.
метод для подсчета угла.
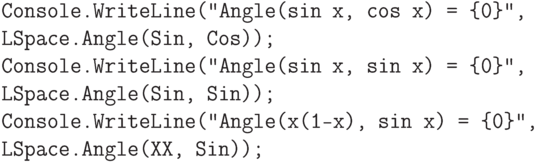
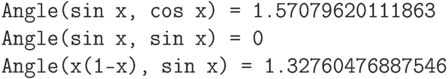
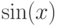 и
и  равен
равен 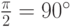 , для таких элементов говорят, что они
ортогональны. А угол между
, для таких элементов говорят, что они
ортогональны. А угол между 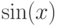 и
и 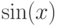 равен нулю, что
предсказуемо.
равен нулю, что
предсказуемо.Ключевые термины
Банахово пространство - полное нормированное пространство.
Гильбертово пространство - полное предгильбертово пространство.
Метрика - функция на паре элементов метрического пространства, соответствующий аналог расстояния между элементами.
Метрическое пространство - абстрактное пространство в котором введена метрика.
Норма - функция на элементах нормированного пространства, аналог длинны.
Нормированное пространство - линейное пространство, в котором введена норма.
Предгильбертово пространство - линейное пространство, в котором введено скалярное произведение.
Скалярное произведение - функция на паре элементов предгильбертова пространства, удовлетворяющая аксиомам скалярного произведения.
Краткие итоги: Рассмотрены наиболее важные понятия функционального анализа - метрические, нормированные, банаховы, гильбертовы пространства. Даны объектно-ориентированные реализации этих пространств. Проведены вычислительные эксперименты, демонстрирующие функциональные пространства.
