Нелиненйые уравнения

Цель лекции: Рассмотреть базовые методы нахождения приближенных решений нелинейных трансцендентных уравнений. Реализовать на C# основной метод.

Решение нелинейных уравнений является одной из самых распространенных задач математики. В лекции, посвященной особенностям вычислительных процедур, мы рассматривали простейший метод решения скалярного уравнения для вычисления корня квадратного из . Этот метод - половинного деления имеет много достоинств. Главным достоинством этого метода является то, что для приближенных решений автоматически получается оценка точности. Второе достоинство данного метода состоит в том, что этот метод легко реализуем. Однако у этого метода есть и недостатки. Для реализации этого метода мы должны знать отрезок, на концах которого функция принимает значения разного знака. А также этот метод является сугубо скалярным и не может быть обобщен на многомерный случай.

Сначала рассмотрим задачу о нахождении корня одного уравнения

Если предположить, что функция является дифференцируемой, и ее производная есть непрерывная функция 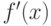, то находить приближенные решения возможно с помощью метода Ньютона. Формулы метода Ньютона получаются из следующих соображений. Пусть 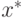- корень функции , а 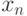некоторое приближение к этому корню. Тогда имеем Если вместо неизвестной точки взять значение 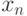, то следующее приближение можно вычислять по формулам Можно показать, что если начальное приближение $ достаточно близко к искомому корню, то итерации, вычисленные по методу Ньютона сходятся к этому корню. К сожалению, это условие носит скорее теоретический характер, поскольку не понятно, что значит "достоаточно близко" и как это условие проверить. Другим достаточным условием сходимости метода Ньютона является условие Также из геометрических соображений можно получить, что итерации сходятся к корню с той стороны, с которой выполнено условие если функция дважды дифференцируема.

Метод Ньютона сходится достаточно быстро, однако у него есть недостатки, состоящие в том, что факт сходимости метода и его скорость сходимости зависят от начального приближения. Вторым серьезным недостатком этого метода является то, что для его реализации нужно знать аналитическое значение производной.

Для устранения последнего недостатка был разработан метод секущих, который иногда называется методом хорд. В этом методе производная заменяется конечной разностью

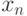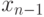Тогда итерации по методу секущих вычисляются по формулам Для реализации метода секущих необходимо знать два предыдущих значения и . Такие методы называются двухшаговыми. Метод секущих сходиться медленнее, чем метод Ньютона, зато этот метод не требуем знания производной функции .

Реализуем класс для вычислений по методу секущих.

В этом классе мы используем класс , реализующий числовые функции. Для начала вычислений необходимо задать два значения и . При инициализации класса следует определить два параметра - максимальное количество итераций и минимальную невязку . Вычисления останавливаются в двух условиях - либо когда превышено количество итераций либо, когда выполнится условие Проведем тестирование нашего метода. Мы будем вычислять корни функции . В результате двух запусков нашего класса мы получим следующие результаты Видно, что если рассматриваемая функция имеет несколько корней, то различные значения начальных приближений могут приводить к различным решениям нашего уравнения.

Рассмотрим теперь вопрос о решении системы трансцендентных уравнений. Пусть необходимо решить следующую систему уравнений

Как правило такие системы решают методом простых итераций. Для этого необходимо систему 13.1 записать в виде Или в векторной форме где $\varphi:\Bbb{R}^n\to\Bbb{R}^n$. Вместо нахождение корня системы 13.1 мы пришли к задаче нахождения неподвижной точки.

Метод простых итераций выглядит довольно просто. Необходимо задать начальное приближение 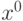, а дальнейшие вычисления проводить по схеме

Однако успех этого метода зависит от свойств функции и начального приближения. Приведем одно достаточное условие сходимости метода простых итераций для случая, когда функции являются непрерывно дифференцируемыми. Построим матрицу с элементами , определяемыми по формулам Достаточным условием сжимаемости отображения $\varphi$ является условие в какой-либо матричной норме. В различных (но эквивалентных) нормах это условие выглядит так или или .

Ключевые термины

Корень функции - точка, в которой функция принимает нулевое значение.

Метод Ньютона - основной итерационный метод для нахождения приближенного решения системы нелинейных уравнений.

Начальное приближение - начальное значение последовательности, которая рассчитывается с помощью рекуррентной процедуры.

Метод секущих - двухшаговый итерационный метод решения нелинейных уравнений без необходимости вычислять производную.

Краткие итоги: Рассмотрены численные методы нахождения приближенных корней трансцендентных уравнений. Приведена объектно-ориентированная реализация наиболее популярных методов нахождения корней уравнений.