Объектно-ориентированная реализация агентного моделирования
Цель лекции: Дать объектно-ориентированную трактовку агентного моделирования. Реализовать это моделирования языке C# и провести разыгрывание полученной модели.
В этой лекции мы будем рассматривать своеобразные динамические системы. Но в отличии от предыдущей лекции мы не будем задавать отображение фазового пространства. Вместо этого мы будем рассматривать множество агентов, которые будут функционировать в заданной внешней для них среде.
Перейдем к формальному описанию. Пусть в нашей системе задано 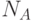 агентов, которых мы будем обозначать:
агентов, которых мы будем обозначать:
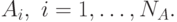
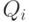 - множество
состояний агента
- множество
состояний агента  ,
, 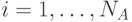 . Кроме того будем
рассматривать множество состояний внешней среды. Это множество
будем обозначать:
. Кроме того будем
рассматривать множество состояний внешней среды. Это множество
будем обозначать: 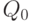 . В этом множестве состояний выделено два
элемента
. В этом множестве состояний выделено два
элемента 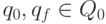 . Элемент
. Элемент  - это начальное
состояние внешней среды, а элемент
- это начальное
состояние внешней среды, а элемент 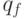 - финальное состояние
системы. Мы будем рассматривать динамическую систему с дискретным
временем
- финальное состояние
системы. Мы будем рассматривать динамическую систему с дискретным
временем 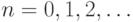 . Введем обозначения
. Введем обозначения  :
: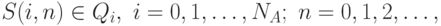
 - это состояние агента (для
- это состояние агента (для 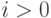 ) или
внешней среды (для
) или
внешней среды (для  ) в момент
) в момент  .
.Внешняя среда в заданном порядке предоставляет право агентам
изменять свое внутреннее состояние и состояние внешней среды. При
этом, разумеется агент имеет право менять состояние внешней среды
не произвольно, а лишь выбирая это состояние из заданных
возможностей. Эти возможности завися как от состояния самого
агента и текущего состояния внешней среды. Введем множества
возможностей  -го агента, находящегося в состоянии
-го агента, находящегося в состоянии 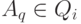 ,
когда внешняя среда находится в состоянии
,
когда внешняя среда находится в состоянии 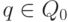 :
:



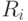 могут быть использованы
генераторы случайных чисел, поэтому выбор "хода" агента может
носить и стохастический характер.
могут быть использованы
генераторы случайных чисел, поэтому выбор "хода" агента может
носить и стохастический характер.Необходимо еще выбрать функцию определения очередности ходов агентов. Обозначим эту функцию через

 ) и от текущего состояния внешней среды.
Часто при разыгрывании ситуации право хода чередуется между
агентами. Однако возможны и более сложные случаи.
) и от текущего состояния внешней среды.
Часто при разыгрывании ситуации право хода чередуется между
агентами. Однако возможны и более сложные случаи.Мы реализуем игру в "крестики-нолики". Рассматривается
квадратное игровое поле  . В игру играют два игрока:
первый ставит отметку "крестиком", второй "ноликом". Цель -
выстроить три крестика или нолика в один ряд или по диагонали.
Игра завершается либо выигрышем одного из игроков, либо вничью,
когда нет более свободных клеток.
. В игру играют два игрока:
первый ставит отметку "крестиком", второй "ноликом". Цель -
выстроить три крестика или нолика в один ряд или по диагонали.
Игра завершается либо выигрышем одного из игроков, либо вничью,
когда нет более свободных клеток.
Поскольку в этой игре известны оптимальные стратегии, при соблюдении которых игра всегда заканчивается вничью, то мы реализуем двух агентов, каждый из которых будем придерживаться разных стратегий.
Стратегия первого игрока. Если свободен центр, ставим играем в центр. Если центр занят, но есть хотя бы один свободный угол, то играем в один из свободных углов, выбирая его случайным образом. Если центр и углы заняты, играем случайным образом в любое свободное поле. Стратегия второго игрока. Всегда играем в любое свободное поле. Интуитивно ясно, что стратегия первого игрока хотя и не является оптимальной, но должна приводить к победе чаще, чем второго.
Мы реализуем данную игру с помощью подхода, основанного на агентного моделирования. Начнем программирование с создания класса, ответственного за игровое поле.
![\begin{verbatim}
class TArray
{
int[] arr;
int Count = 9;
public TArray()
{
arr = new int[9];
for (int i = 0; i < 9; i++)
{
arr[i] = 0;
}
}
public bool Check(int i, int Star)
{
if (Who(i) == 0)
{
arr[i] = Star;
Count--;
return true;
}
else
{
return false;
}
}
\end{verbatim}](/sites/default/files/tex_cache/a8f5e7811d0607419ece2dd0e7af9269.png)
![\begin{verbatim}
public int GetCount()
{
return Count;
}
public int Who(int i)
{
return arr[i];
}
public bool IsOver(int Star)
{
int i;
for(i=0;i<3;i++)
{
if ((arr[i] == Star) &&
(arr[i + 1] == Star) && (arr[i + 2] == Star))
{
return true;
}
if ((arr[i] == Star) &&
(arr[i + 3] == Star) && (arr[i + 6] == Star))
{
return true;
}
}
\end{verbatim}](/sites/default/files/tex_cache/fc3bc7dfed8c01d4edb21cd69bd75ef0.png)
![\begin{verbatim}
if ((arr[0] == Star) &&
(arr[4] == Star) && (arr[8] == Star))
{
return true;
}
if ((arr[2] == Star) &&
(arr[4] == Star) && (arr[6] == Star))
{
return true;
}
return false;
}
}
\end{verbatim}](/sites/default/files/tex_cache/c0402a0addfe61f440a70859b8cdc947.png)
Этот класс хранит текущую позицию и умеет найти выигрышную позицию, если она сложилась на игровом поле. Этот класс предоставляет информацию о текущей позиции и возвращает количество свободных клеток.
