Приближение многочленами
Цель лекции: Рассмотреть основные методы аппроксимации числовых функций полиномами. Описать методы полиномиальной интерполяции функций.
Довольно часто возникает задача восстановление значений функции, которая задана лишь в некоторых точках. Совершенно очевидно, что если мы знаем значения функции лишь в некоторых фиксированных точках, то значения функции в промежуточных значениях аргумента могут быть любыми. Однако часто имеется некоторая априорная информация о свойствах функции, с помощью которой удается найти приемлемое значение функции.
Пусть на отрезке ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) задана некоторая числовая функция
задана некоторая числовая функция  . Разбиением отрезка
. Разбиением отрезка ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) называется конечное множество
точек
называется конечное множество
точек  таких, что
таких, что

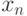 мы будем называть узловыми точками. Пусть также
на ряду с разбиением отрезка нам дан набор чисел
мы будем называть узловыми точками. Пусть также
на ряду с разбиением отрезка нам дан набор чисел 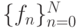 , который имеет смысл значений функции в узловых
точках
, который имеет смысл значений функции в узловых
точках 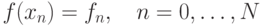 .
Задача интерполяции состоит в том, чтобы найти значение
функции
.
Задача интерполяции состоит в том, чтобы найти значение
функции  в произвольной точке
в произвольной точке ![x\in[a,b]](/sites/default/files/tex_cache/c7c42309c359c25dfe77f397d5261997.png) . Несколько реже
возникает задача экстраполяции состоящей в том, чтобы найти
значение функции
. Несколько реже
возникает задача экстраполяции состоящей в том, чтобы найти
значение функции  в точке
в точке ![x\notin[a,b]](/sites/default/files/tex_cache/88b6f307d5be729ea91741e247bb2b7c.png) . Мы будем в основном
рассматривать задачу интерполяции.
. Мы будем в основном
рассматривать задачу интерполяции.Решение задачи интерполяции может быть представлено в виде функции (алгоритма)
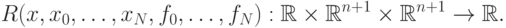
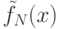 , которая определена на всем отрезке
, которая определена на всем отрезке ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Эта функция называется интерполяционной.
. Эта функция называется интерполяционной.Классическим методом построения интерполяционной функции является
построение многочлена степени 
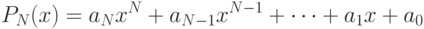
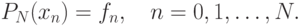
 .
.Покажем, что такой многочлен всегда можно построить. Точнее мы предъявим формулу, которая даст нам этот интерполяционный многочлен.
Введем функции:
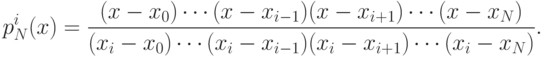
 .
Непосредственно из этой формулы мы имеем следующие соотношения
.
Непосредственно из этой формулы мы имеем следующие соотношения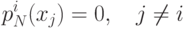

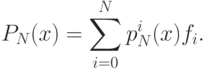 |
( 14.1) |
Можно убедиться также в том, что этот многочлен единственный. Действительно, для любого другого многочлена, для которого

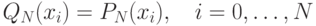 .
Тогда многочлен
.
Тогда многочлен  имеет степень не большую,
чем
имеет степень не большую,
чем  , а также имеет
, а также имеет 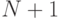 корней. По основной теореме алгебры
этот многочлен
корней. По основной теореме алгебры
этот многочлен 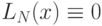 .
.Многочлен, заданный по формуле 14.1 называется интерполяционным многочленом в форме Лагранжа.
Лагранжева форма интерполяционного многочлена является не единственной формой интерполяционного многочлена. Более удобной для практических расчетов является интерполяционный многочлен в форме Ньютона. Для заданного разбиения отрезка и значений функции в этих узлах введем понятие раздельной разности. Раздельной разностью первого порядка называется число

 -го порядка определяется по
рекуррентной формуле
-го порядка определяется по
рекуррентной формуле
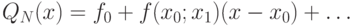

Хотя формулы для построения интерполяционных многочленов выглядят
просто, метод интерполяции функций многочленами имеет серьезные
недостатки для больших значений  . Во-первых, работа с
многочленами большой степени, как правило, сопряжено с
вычислительной неустойчивостью. Во-вторых, как было показано
К.Рунге в своей знаменитой работе 1901 года, существует такая
бесконечно гладкая функция, для которой интерполяционный
многочлен, построенный на равномерной сетке может иметь бесконечно
большое отклонение с увеличением количества узловых точек.
. Во-первых, работа с
многочленами большой степени, как правило, сопряжено с
вычислительной неустойчивостью. Во-вторых, как было показано
К.Рунге в своей знаменитой работе 1901 года, существует такая
бесконечно гладкая функция, для которой интерполяционный
многочлен, построенный на равномерной сетке может иметь бесконечно
большое отклонение с увеличением количества узловых точек.
Рассмотрим этот пример. Пусть функция

![[-1,1]](/sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png) . Это функция обладает почти всеми
"хорошими" свойствами. Для каждого
. Это функция обладает почти всеми
"хорошими" свойствами. Для каждого  введем узловые точки по
формуле
введем узловые точки по
формуле
 введем интерполяционный многочлен, построенный по
формуле 14.1. К.Рунге было показано, что для этого
случая имеет место
введем интерполяционный многочлен, построенный по
формуле 14.1. К.Рунге было показано, что для этого
случая имеет место![\lim\limits_{N\to\infty}\max\limits_{x\in[-1,1]}|f(x)-P_N(x)|=\infty.](/sites/default/files/tex_cache/296d0647d3dc5bcbd4126503c0ea99be.png)
Ключевые термины
Разбиение отрезка - конечное множество точек, принадлежащих заданному отрезку.
Узловые точки - элементы из множества разбиения отрезка.
Интерполяция - процедура приближенного вычисления значений функции по заданным значениям функции в узловых точках.
Экстраполяция - процедура вычисления значений функции вне отрезка, на котором задана функция.
Интерполяционная функция - функция, которая реализует интерполяцию.
Краткие итоги: Рассмотрены методы интерполяции функции на основе приближения полиномами. Приведены методы построения интерполяционных полиномов в форме Лагранжа и в форме Ньютона.
