Эволюционные уравнения в частных производных
Цель лекции: Рассмотреть методы построения приближенных решений для линейных и нелинейных эволюционных уравнений.
В предыдущей лекции мы рассматривали системы обыкновенных дифференциальных уравнений конечной размерности. Однако многие процессы в нашем мире описываются бесконечными системами дифференциальных уравнений. Такие системы иногда называют распределенными системами или уравнениями в частных производных. Решением уравнений в частных производных является функция многих переменных. Простейшими уравнениями в частных производных второго порядка являются следующие уравнения
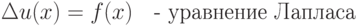
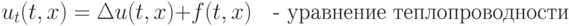
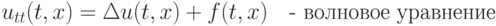
Мы будем рассматривать эволюционные уравнения относительно функций
заданных на отрезке ![[0,T]](/sites/default/files/tex_cache/b74093923941d33ee19becc5f4b48b25.png) со значениями в банаховом
пространстве, например, в пространстве
со значениями в банаховом
пространстве, например, в пространстве ![C[a,b]](/sites/default/files/tex_cache/d930e3053f32dbc51f14e870df59674d.png) . Численные методы,
которые мы будем рассматривать могут быть одинаково эффективно
применены как для линейных, так и для нелинейных уравнений.
Рассмотрим математическую постановку начальной задачи. Пусть
. Численные методы,
которые мы будем рассматривать могут быть одинаково эффективно
применены как для линейных, так и для нелинейных уравнений.
Рассмотрим математическую постановку начальной задачи. Пусть  есть некоторое банахово пространство. Пусть в этом в этом
пространстве задано множество
есть некоторое банахово пространство. Пусть в этом в этом
пространстве задано множество  , на котором определен
оператор
, на котором определен
оператор 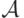 (линейный или нелинейный).
(линейный или нелинейный).
Будем рассматривать уравнение
![u_t(t)={\cal A} u(t),\quad t\in[0,T]](/sites/default/files/tex_cache/8fbedcbe1a204b0e0d66e6a886abf30f.png) |
( 16.5) |
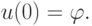 |
( 16.6) |
![u\in C^1([0,T];X)](/sites/default/files/tex_cache/002230a14e887754c5ee22ce0e539ec5.png) такая, что
такая, что  при
всех
при
всех ![t\in[0,T]](/sites/default/files/tex_cache/8b20560d8c06799d96af194ac2594a0b.png) и, удовлетворяющая
16.5-16.6. Элемент
и, удовлетворяющая
16.5-16.6. Элемент  называется начальным условием, а задача
16.5-16.6 называется абстрактной
задачей Коши.
называется начальным условием, а задача
16.5-16.6 называется абстрактной
задачей Коши.Приведем два характерных примера таких задач. В качестве
пространства  мы возьмем пространство непрерывных функций
мы возьмем пространство непрерывных функций ![C[0,2\pi]](/sites/default/files/tex_cache/7fb2e70f009b8d4813961789d8ff8a90.png) в качестве множества
в качестве множества 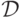 возьмем множество непрерывно
дифференцируемых функций на отрезке
возьмем множество непрерывно
дифференцируемых функций на отрезке ![[0,2\pi]](/sites/default/files/tex_cache/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) и являющихся
и являющихся 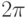 -периодическими. Будем рассматривать два модельных
уравнения. Первое - уравнение линейного переноса
-периодическими. Будем рассматривать два модельных
уравнения. Первое - уравнение линейного переноса
 |
( 15.7) |
 - постоянная, имеющая смысл "скорости"
распространения волны. Второе уравнение - уравнение нелинейного
переноса
- постоянная, имеющая смысл "скорости"
распространения волны. Второе уравнение - уравнение нелинейного
переноса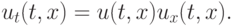 |
( 15.8) |
Опишем построение численной схемы. Мы будем использовать проекционный метод для приближенного решения абстрактной задачи
Коши. Этот метод позволяет свести задачу к системе обыкновенных
дифференциальных уравнений. Пусть для любого  существует пара
отображений
существует пара
отображений



 . Задача
16.5-16.6 заменяется следующей задачей
. Задача
16.5-16.6 заменяется следующей задачей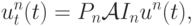 |
( 16.9) |
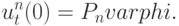 |
( 16.10) |
 -го
порядка. Далее эта система решается стандартными численными
методами, например, методом Рунге-Кутта, который мы рассматривали
на прошлой лекции. После нахождения решения задачи
16.9-16.10 то есть функции
-го
порядка. Далее эта система решается стандартными численными
методами, например, методом Рунге-Кутта, который мы рассматривали
на прошлой лекции. После нахождения решения задачи
16.9-16.10 то есть функции  , в
качестве приближенным решением исходной задачи можно выбрать
функцию
, в
качестве приближенным решением исходной задачи можно выбрать
функцию 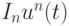 .
.Хотя описанный проекционный метод является, как правило, легко
реализуемым, но при его использовании необходимо иметь в виду
вопросы, связанные с его сходимостью и устойчивостью. Дело в том,
что даже для простейших уравнений при использовании проекционного
метода следует согласовывать шаг по времени, то есть тот шаг,
который используется в численном методе при решении задачи
16.9-16.10, с шагом, который имеет место при
построении аппроксимации пространства  .
.
Для уравнений 16.7 и 16.8 мы будем
использовать следующие операторы 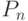 и
и 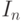
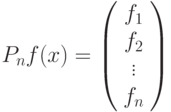
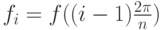 ,
,  . Для реализации
оператора
. Для реализации
оператора 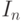 необходимо использовать подходящую интерполяцию.
Мы будем рассматривать кусочно-линейную интерполяцию. Покажем, как
таким образом можно определить операцию
необходимо использовать подходящую интерполяцию.
Мы будем рассматривать кусочно-линейную интерполяцию. Покажем, как
таким образом можно определить операцию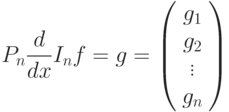

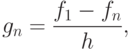
 .
.Реализуем этот метод для линейного уравнения переноса. Для этого
мы создадим класс, являющийся наследником от класса  .
.
![\begin{verbatim}
class TCUEvol : TRungeKutta
{
double c; // скорость волны
double h;
public TCUEvol(int N, double c) : base(N)
{
this.c = c;
h = 2.0 * Math.PI / N;
}
public override void F(double t, double[] Y, ref double[] FY)
{
int i;
for (i = 0; i < N - 1; i++)
{
FY[i] = c * (Y[i + 1] - Y[i]) / h;
}
FY[N - 1] = c * (Y[0] - Y[N - 1]) / h;
}
}
\end{verbatim}](/sites/default/files/tex_cache/7da3d5800d38fa8f80adbb20ae2d1b5d.png)
Испытаем наш класс, учитывая, что для начальной функции вида 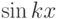 это уравнение имеет точное решение в виде бегущей волны
это уравнение имеет точное решение в виде бегущей волны  .
.
![\begin{verbatim}
int N = 1000;
double h = 0.0001;
double[] Y0 = new double[N];
TCUEvol CU = new TCUEvol(N, 1);
double x;
int i;
for (i = 0; i < N; i++)
{
x = (double)i * (2.0 * Math.PI) / (double)N;
Y0[i] = Math.Sin(5.0 * x);
}
CU.SetInit(0, Y0);
double t = 0;
while (CU.GetCurrent() < (1.0 + h / 2.0))
{
t = CU.GetCurrent();
CU.NextStep(h); // рассчитать на следующем шаге
}
StreamWriter Fout = File.CreateText("cu.txt");
for (i = 0; i < N; i++)
{
x = (double)i * (2.0 * Math.PI) / (double)N;
Fout.WriteLine("{0}\t{1}\t{2}\t{3}", x, CU.Y[i],
Math.Sin(5.0 * (t + x)), Math.Sin(5.0 * (t + x)) - CU.Y[i]);
}
Fout.Close();
\end{verbatim}](/sites/default/files/tex_cache/bc0d62333c3b7c301e105e04b67f4781.png)
Мы решали задачу:
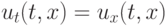

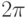 -периодическими по переменной
-периодическими по переменной  условиями
имеет единственное решение
условиями
имеет единственное решение
