Приближение сплайнами
Цель лекции: Описать стандартные методы построения кубических сплайнов. Реализовать на языке C# процедуру интерполирования функций с помощью кубических сплайнов.
В предыдущей лекции мы рассматривали приближение функций с помощью многочленов. Многочлены являются бесконечно гладкими функциями. С одной стороны это может показаться достоинством интерполяционного метода. Однако на практике это достоинство часто оборачивается недостатком. Налагая на интерполяционную функцию столь большие ограничения, мы неизбежно сталкиваемся с проблемой устойчивости. Чаще гораздо более выгодно использовать в качестве интерполирующих функций меньшие требования гладкости, но получать более эффективные численные решения. Тем более, что во многих задачах, где возникают вопросы интерполяции, требования бесконечной гладкости являются неестественными.
Наиболее успешными средствами интерполяции числовых функций являются методы, основанные на сплайн-интерполяции. Термин "сплайн" происходит от названия гибкой рейки, с помощью которой проводят гладкие кривые через заданные точки. В заданных точках сплайн закреплялся физически. В математике под сплайном понимают интерполирующую функцию, производные которой могут иметь разрывы в узловых точках. Классическим вариантом сплайна является кубические сплайны. Эти сплайны иногда называют сплайнами Шёнберга по имени математика, который ввел эти сплайны на современном уровне. Кубические сплайны представляют собой дважды непрерывно дифференцируемые функции, которые на отрезка между соседними узлами являются кубическими многочленами.
Пусть также дано разбиение отрезка ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , и значения функции в
узлах
, и значения функции в
узлах

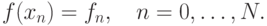
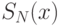 ,
, ![x\in[a,b]](/sites/default/files/tex_cache/c7c42309c359c25dfe77f397d5261997.png) , что для этой функции выполнены следующие условия:
, что для этой функции выполнены следующие условия:-
 ,
, 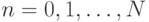 .
. -
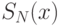 ,
,  ,
, 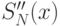 являются непрерывными функциями.
являются непрерывными функциями. - На каждом отрезке
![[x_{n-1},x_n]](/sites/default/files/tex_cache/c29a40d45feaeee6ef8b9faeac873acb.png) ,
, 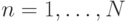 функция
функция 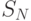 представима в виде
представима в виде![S_N(x)=a^n_3x^3+a^n_2x^2+a^n_1x+a^n_0,\quad x\in[x_{n-1},x_n],
n=1,\dots,N.](/sites/default/files/tex_cache/16c913d554b3cb3ca3f63e29cfd7ed64.png)
Как мы увидим в дальнейшем - для однозначного задания сплайна нам необходимо дополнительно добавить краевые условия на искомый сплайн. Мы будем рассматривать наиболее характерные условия:
-
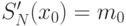 ,
,  .
. -
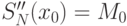 ,
,  .
.
Перейдем к вопросу построения сплайна. Разумеется для того, чтобы
задать сплайн необходимо вычислить набор коэффициентов  ,
,  ;
; 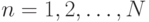 . Однако этот путь является
неэффективным. Дело в том, что эти коэффициенты не являются
независимыми - на них наложены условия, чтобы обеспечить
непрерывность и непрерывную дифференцируемость первых и вторых
производных. Мы будем использовать для задания сплайнов другой
подход.
. Однако этот путь является
неэффективным. Дело в том, что эти коэффициенты не являются
независимыми - на них наложены условия, чтобы обеспечить
непрерывность и непрерывную дифференцируемость первых и вторых
производных. Мы будем использовать для задания сплайнов другой
подход.
Введем обозначение
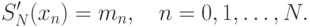
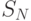 в следующей форме
в следующей форме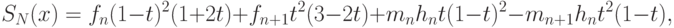
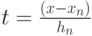 ,
, 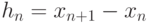 .
.Условия непрерывности второй производной сплайна определяют систему линейных уравнений
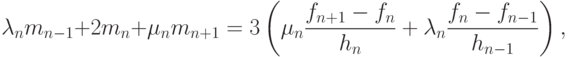 |
( 15.1) |

 |
( 15.2) |
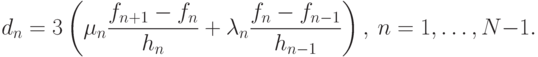
 ,
а для условий второго типа
,
а для условий второго типа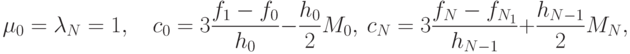
Как мы уже отмечали, система 15.2 представляет собой систему линейных алгебраических уравнений. Однако матрица, определяющая эту систему является трехдиагональной. Для решения таких уравнений будем применять уже известный нам метод прогонки.
Приведем реализацию нашего класса
![\begin{verbatim}
class TSpline
{
double[] Xn;
int N;
TRFunc f;
TProgon Progon;
double[] m;
public TSpline(double[] Xn, TRFunc f)
{
this.N = Xn.Count();
this.Xn = Xn;
this.f = f;
}
double h(int n)
{
return Xn[n+1] - Xn[n];
}
double mu(int n)
{
return h(n - 1) / (h(n - 1) + h(n));
}
double la(int n)
{
return 1 - mu(n);
}
\end{verbatim}](/sites/default/files/tex_cache/7da5a73148266d829aa2940ef506a921.png)
![\begin{verbatim}
public void Build(double m0, double mN)
{
Progon = new TProgon();
Progon.a = new double[N];
Progon.b = new double[N];
Progon.c = new double[N];
Progon.d = new double[N];
int n;
for (n = 1; n < N-1; n++)
{
Progon.a[n] = 2.0;
Progon.b[n] = la(n);
Progon.c[n] = mu(n);
Progon.d[n] = 3.0 * (mu(n) * (f.CalcY(Xn[n + 1])
- f.CalcY(Xn[n])) / h(n) +
la(n) * (f.CalcY(Xn[n]) -
f.CalcY(Xn[n - 1])) / h(n - 1));
}
Progon.a[0] = 2;
Progon.a[N-1] = 2;
Progon.b[0] = 0;
Progon.b[N-1] = 0;
Progon.c[0] = 0;
Progon.c[N-1] = 0;
Progon.d[0] = 2 * m0;
Progon.d[N-1] = 2 * mN;
Progon.CalcZ();
}
\end{verbatim}](/sites/default/files/tex_cache/ffb123f37bab7212bda7f157b15fa326.png)
![\begin{verbatim}
public double CalcSpline(double x)
{
int n;
for (n = 0; n < N-2; n++)
{
if ((x >= Xn[n]) && (x < Xn[n + 1]))
{
break;
}
}
double t = (x - Xn[n]) / h(n);
return f.CalcY(Xn[n]) * (1 - t) * (1 - t) * (1 + 2 * t) +
f.CalcY(Xn[n + 1]) * t * t * (3 - 2 * t) +
Progon.z[n] * h(n) * t * (1 - t) * (1 - t) -
Progon.z[n + 1] * h(n) * t * t * (1 - t);
}
}
\end{verbatim}](/sites/default/files/tex_cache/8e0129f679d3401f2fcadfeb62ca63ba.png)
Теперь испытаем наш сплайн на функции 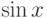 . Мы будем строить
сплайн всего по шести точкам.
. Мы будем строить
сплайн всего по шести точкам.
![\begin{verbatim}
TSinFunc F = new TSinFunc(0, 2 * Math.PI);
int n;
int N = 5;
double[] Xn = new double[N + 1];
double dx = (F.Get_b() - F.Get_a()) / (double)N;
for (n = 0; n <= N; n++)
{
Xn[n] = F.Get_a() + (double)n * dx;
}
TSpline Spline = new TSpline(Xn, F);
Spline.Build(1, 1);
\end{verbatim}](/sites/default/files/tex_cache/2c0d842e276837f3bbc9fc4da0be44f5.png)

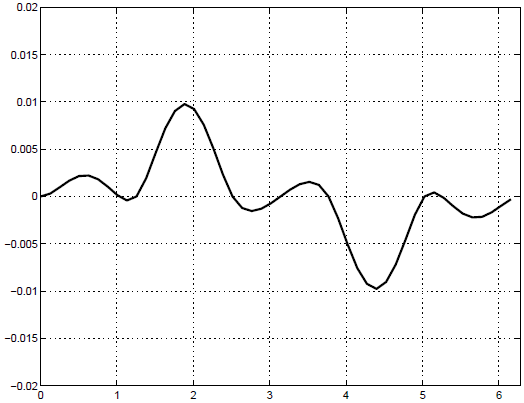
На рисунке 15.1 мы приводим погрешность нашей интерполяции.
Наибольшая погрешность не превосходит 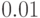 , что оказывается
очень неплохим результатом.
, что оказывается
очень неплохим результатом.
Ключевые термины
Сплайн - интерполяционная функция, производные которой могут иметь разрывы в узловых точках.
Кубические сплайны - сплайны, которые являются кубическими многочленами между соседними узловыми точками и являются дважды непрерывно дифференцируемыми.
Краткие итоги: Рассмотрены методы интерполяции функций на основе кубических сплайнов. Приведена объектно-ориентированная реализация построение кубического сплайна.