Опубликован: 18.05.2011 | Доступ: свободный | Студентов: 976 / 106 | Оценка: 4.40 / 4.20 | Длительность: 12:30:00
Тема: Программирование
Специальности: Программист, Архитектор программного обеспечения
Теги:
Лекция 18:
Эволюционные уравнения в частных производных
Лабораторная работа "Дифференциальные уравнения"
Цель занятия
Выяснить как ведут себя численные методы решения обыкновенных дифференциальных уравнений в случаях, когда отсутствует решение задачи.
Сценарий лабораторной работы
- Рассмотреть задачу Коши
 которая не имеет решения на отрезке
которая не имеет решения на отрезке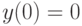
![[0,T]](/sites/default/files/tex_cache/b74093923941d33ee19becc5f4b48b25.png) , если
, если 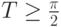 .
. - Написать программу на основе метода Рунге-Кутта.
- Провести вычислительные опыты по приближенному решению этой задачи Коши на отрезках различной длинны.
- Рассмотрите различные нелинейные уравнения в ограниченной области. С помощью вычислительных опытов найдите время выхода решения на границу области.
- Для уравнений с известными решениями - сравните это время с результатами численных опытов.
Указания
Для обыкновенных дифференциальных уравнений решение может "уходить на бесконечность" за конечное время. При этом правая часть таких уравнений может быть бесконечно дифференцируемой, и определенной во всем пространстве. При этом такие численные методы, как Рунге-Кутта могут быть реализованы для любого временного интервала. Однако в ходе выполнения программы может возникнуть переполнение.
Заметим, что C#, точнее .NET Framework, умеет корректно работать со значением "бесконечность". В случае, когда возникнет такое значение, можно говорить, что метод "заметил" отсутствие решения.
