Эволюционные уравнения в частных производных
Практическое занятие "Дифференциальные уравнения"
Цель занятия
Выяснить как ведут себя численные методы решения обыкновенных дифференциальных уравнений в случаях, когда отсутствует решение задачи.
Практическая задача
В соответствующей лекции мы рассматривали метод Рунге-Кутта для построения приближенных решений задачи Коши для системы обыкновенных дифференциальных уравнений. Сейчас мы рассмотрим некоторые примеры численных опытов.
Мы уже отмечали, что задача Коши

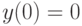
![[0,T]](/sites/default/files/tex_cache/b74093923941d33ee19becc5f4b48b25.png) , где
, где 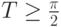 .
Посмотрим как себя поведет численный метод Эйлера при попытке
решить эту задачу на отрезке
.
Посмотрим как себя поведет численный метод Эйлера при попытке
решить эту задачу на отрезке ![[0,2]](/sites/default/files/tex_cache/70fd3f388413505934da60b43afc4088.png) . Выполним следующий код,
используя написанный ранее класс
. Выполним следующий код,
используя написанный ранее класс  .
.![\begin{verbatim}
double h = 0.1;
double[] Y0 = { 0 };
TTest1Euler Test1Euler = new TTest1Euler();
Test1Euler.SetInit(0, Y0);
while (Test1Euler.GetCurrent() < (2.0 + h / 2.0))
{
Console.WriteLine("{0}\t{1}", Test1Euler.GetCurrent(),
Test1Euler.Y[0]);
Test1Euler.NextStep(h);
}
\end{verbatim}](/sites/default/files/tex_cache/a823d36ca955634db21f0c0c67685f44.png)
Здесь используется следующий класс  .
.
![\begin{verbatim}
class TTest1Euler : TEuler
{
public TTest1Euler() : base(1) { }
public override void F(double t, double[] Y, ref double[] FY)
{
FY[0] = Y[0] * Y[0] + 1.0;
}
}
\end{verbatim}](/sites/default/files/tex_cache/374985dfb6d5e821075771ccb9533f1c.png)
Сначала мы используем нарочито грубый шаг по времени. Поэтому вот результат:

Мы видим, что наш метод в шагом  практически "не
чувствует", что решения уже не существует. Теперь уменьшим шаг на
порядок - возьмем
практически "не
чувствует", что решения уже не существует. Теперь уменьшим шаг на
порядок - возьмем  . В результате получим следующее.
. В результате получим следующее.


Мы видим, что C#, точнее .NET Framework, довольно корректно использовали значение "бесконечность". В этом случае уже можно говорить, что наш метод "заметил" отсутствие решения.
Теперь мы рассмотрим поведение нашего численного метода в случае, когда имеет место разрыв правой части по фазовым переменным. В этом случае поведение решений может быть по разному. Возможны случаи, когда уравнение имеет разрывные траектории, а возможны и случаи, когда уравнение не имеет решений. В последнем случае используют аппроксимацию дифференциального уравнения дифференциальным включением. Однако мы рассмотрим применение нашего метода Эйлера "в лоб" для задачи Коши


![\begin{verbatim}
class TTest2Euler : TEuler
{
public TTest2Euler() : base(1) { }
public override void F(double t, double[] Y,
ref double[] FY)
{
FY[0] = 1.0 - 2 * sign(Y[0]);
}
double sign(double x)
{
if (x >= 0)
{
return 1;
}
else
{
return -1;
}
}
}
\end{verbatim}](/sites/default/files/tex_cache/9b682d94430b65d17b5415caa06b899c.png)
Запустим наш класс с шагом  на отрезке
на отрезке ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) . Вот
результат.
. Вот
результат.

