Эволюционные уравнения в частных производных
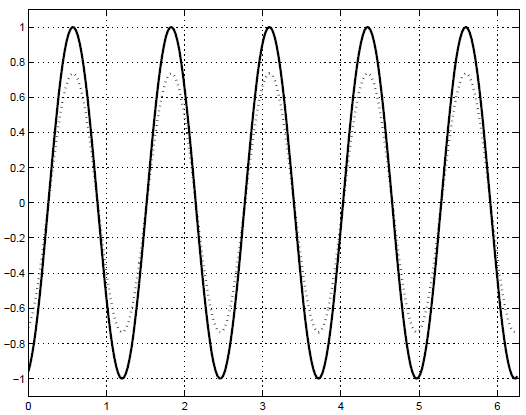
в чем можно убедится непосредственно. На рисунке 17.1 мы приводим
графики точного решения (сплошной линией) и приближенного
(точечной линией) при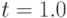 
. Результат нашего вычислительного
опыта не является удовлетворительным. Мы видим хорошее совпадение
фазы решений, но амплитуда приближенного решения меньше точного.
Наша схема оказалась весьма диссипативной, что делает ее
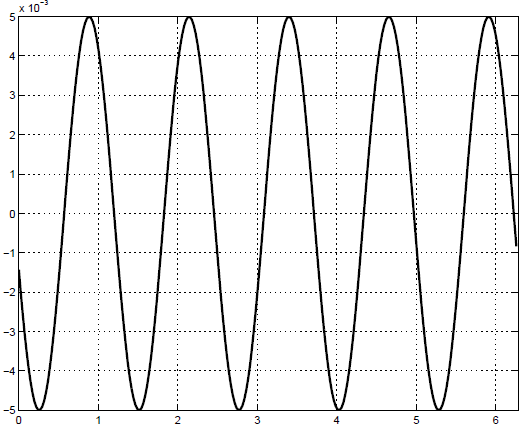
непригодной. На рисунке 17.2 мы приведем погрешность приближенного
решения.
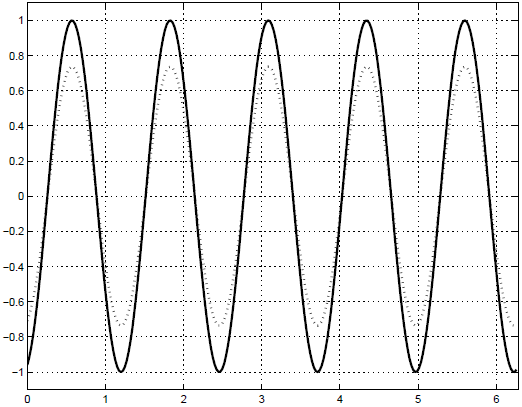
Рис. 17.2. Погрешность приближенного решения уравнения линейного переноса с помощью кусочно-линейной интерполяции
Покажем как можно существенно повысить точность нашего метода. Для
этого мы воспользуемся так называемыми аналитико-числовыми
методами. Суть этих методов состоит в том, что ряд операций,
можно выполнить точно. Например в известной нам уже задаче
дифференцирования функции. Пусть нам нужно найти производную
функции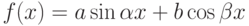 
. При программировании
нам выгодно задавать не поточечные значения этой функции, а всего
четыре коэффициента - 
, 
, 
и 
. Обозначим
эти коэффициенты четырьмя переменными:
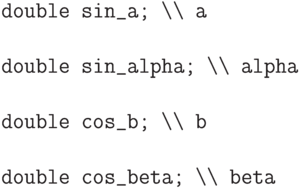
Тогда производная функци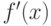и 
имеет такой же вид и может быть
также представлена такими же коэффициентами:
Вычислить коэффициенты производной можно следующим образом
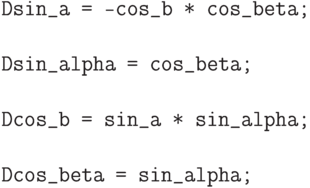
При это, если не считать возможные ошибки округления при умножении, операция дифференцирования была выполнена безукоризненно.
С другой стороны гладкие (например, кусочно дифференцируемые и имеющие ограниченные производные) периодические функции могут быть разложены в ряд Фурье, а ряд Фурье представляет собой комбинацию рассмотренных выше функций. Поэтому, если задавать функцию коэффициентами Фурье, то такие операции как дифференцирование и интегрирование можно выполнять фантастически быстро. Чем более гладкая функция, тем быстрее коэффициенты Фурье сходятся к нулю. Следовательно, часто ряд Фурье удается аппроксимировать конечными тригонометрическими суммами.
Реализуем новый класс в котором мы будем применять численно-аналитические методы.
![\begin{verbatim}
class TCUAn : TRungeKutta
{
double c;
double h;
public TCUAn(int N, double c)
: base(N)
{
this.c = c;
h = 2.0 * Math.PI / N;
}
public double GetY(double x)
{
double res = 0;
int i;
double di;
for (i = 1; i < (N - 1) / 2; i++)
{
di = (double)i;
res += Math.Sin(di * x) * Y[i - 1];
res += Math.Cos(di * x) * Y[N - i];
}
res += Y[(N - 1) / 2];
return res;
}
\end{verbatim}](/sites/default/files/tex_cache/dd67e628c7cb765eefb9699cfb6027ec.png)
![\begin{verbatim}
public override void F(double t, double[] Y, ref double[] FY)
{
Diff(Y, ref FY);
int i;
for (i = 0; i < N; i++)
{
FY[i] = c * FY[i];
}
}
void Diff(double[] Y, ref double[] DY)
{
int i;
double di;
for (i = 1; i < (N-1) / 2; i++)
{
di = (double)i;
DY[i - 1] = -di * Y[N - i];
DY[N - i] = di * Y[i - 1];
}
DY[(N - 1) / 2] = 0;
}
}
\end{verbatim}](/sites/default/files/tex_cache/11a47de9cded61fcdd21bc7e32cbfeea.png)
В этом классе мы добавили новые методы - для дифференцирования функции, а также для суммирования тригонометрической суммы. Заметим, что мы рассматриваем систему дифференциальных уравнений относительно коэффициентов Фурье. Испытаем наш класс.
![\begin{verbatim}
int N = 257;
double h = 0.001;
double[] Y0 = new double[N];
TCUAn CUAn = new TCUAn(N, 1);
for (i = 0; i < N; i++)
{
Y0[i] = 0;
}
Y0[4] = 1;
CUAn.SetInit(0, Y0);
t = 0;
while (CUAn.GetCurrent() < (1.0 + h / 2.0))
{
t = CUAn.GetCurrent();
CUAn.NextStep(h);
}
Fout = File.CreateText("cuan.txt");
for (i = 0; i < N; i++)
{
x = (double)i * (2.0 * Math.PI) / (double)N;
Fout.WriteLine("{0}\t{1}\t{2}\t{3}", x, CUAn.GetY(x),
Math.Sin(5.0 * (t + x)), Math.Sin(5.0 * (t + x))
- CUAn.GetY(x));
}
Fout.Close();
\end{verbatim}](/sites/default/files/tex_cache/45c677cdb1e809bb490cde6464a7ca01.png)
На рисунке 17.3 мы приводим погрешность приближенного решения.
