Обыкновенные дифференциальные уравнения
Перейдем к реализации метода Рунге-Кутта на основе нашего класса 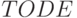 .
.
![\begin{verbatim}
abstract class TRungeKutta : TODE
{
double[] Y1, Y2, Y3, Y4; // внутренние переменные
public TRungeKutta(int N) : base(N)
{
Y1 = new double[N];
Y2 = new double[N];
Y3 = new double[N];
Y4 = new double[N];
}
\end{verbatim}](/sites/default/files/tex_cache/af225795c13e7d7f31aebdc40d9e5193.png)
![\begin{verbatim}
// следующий шаг метода Рунге-Кутта, dt - шаг по времени
override public void NextStep(double dt)
{
if (dt < 0)
{
return;
}
int i;
F(t, Y, ref Y1); // рассчитать Y1
for (i = 0; i < N; i++)
{
YY[i] = Y[i] + Y1[i] * (dt / 2.0);
}
F(t + dt / 2.0, YY, ref Y2); // рассчитать Y2
for (i = 0; i < N; i++)
{
YY[i] = Y[i] + Y2[i] * (dt / 2.0);
}
F(t + dt / 2.0, YY, ref Y3); // рассчитать Y3
for (i = 0; i < N; i++)
{
YY[i] = Y[i] + Y3[i] * dt;
}
F(t + dt, YY, ref Y4); // рассчитать Y4
for (i = 0; i < N; i++)
{
// рассчитать решение на новом шаге
Y[i] = Y[i] + dt / 6.0 *
(Y1[i] + 2.0 * Y2[i] + 2.0 * Y3[i] + Y4[i]);
}
t = t + dt; // увеличить шаг
}
}
\end{verbatim}](/sites/default/files/tex_cache/8a5db1b1c109504f5fb24788bfe162d1.png)
Теперь протестируем наши методы на примере задач Коши, описывающей гармонические колебания математического маятника. Мы решаем следующую задачу.
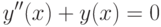


 . Чтобы
применить к этой задаче наши методы нужно записать ее в виде
системы уравнений первого порядка.
. Чтобы
применить к этой задаче наши методы нужно записать ее в виде
системы уравнений первого порядка.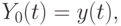
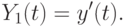

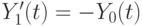 с начальными условиями
с начальными условиями

![\begin{verbatim}
class THarmonicEuler : TEuler
{
public THarmonicEuler() : base(2) { }
public override void F(double t, double[] Y,
ref double[] FY)
{
FY[0] = Y[1];
FY[1] = -Y[0];
}
}
class THarmonicRK : TRungeKutta
{
public THarmonicRK() : base(2) { }
public override void F(double t, double[] Y,
ref double[] FY)
{
FY[0] = Y[1];
FY[1] = -Y[0];
}
}
\end{verbatim}](/sites/default/files/tex_cache/8ee7abbc773a301682b26671369192b7.png)
Испытаем наши классы
![\begin{verbatim}
double h = 0.1;
double[] Y0 = { 0, 1.0 };
THarmonicEuler HarmonicEuler = new THarmonicEuler();
HarmonicEuler.SetInit(0, Y0);
THarmonicRK HarmonicRK = new THarmonicRK();
HarmonicRK.SetInit(0, Y0);
StreamWriter F = File.CreateText("harmonic.txt");
double t, Euler, RK, Sin;
while (HarmonicEuler.GetCurrent() < (2 * Math.PI + h / 2.0))
{
t = HarmonicEuler.GetCurrent();
Euler = HarmonicEuler.Y[0];
RK = HarmonicRK.Y[0];
Sin = Math.Sin(t);
F.WriteLine("{0}\t{1}\t{2}\t{3}\t\t{4}\t{5}\t{6}",
t, Euler, RK, Sin, t, Math.Abs(Sin - Euler),
Math.Abs(Sin - RK));
HarmonicEuler.NextStep(h);
HarmonicRK.NextStep(h);
}
F.Close();
\end{verbatim}](/sites/default/files/tex_cache/af147d4a541de6845593842f1a7ddc97.png)
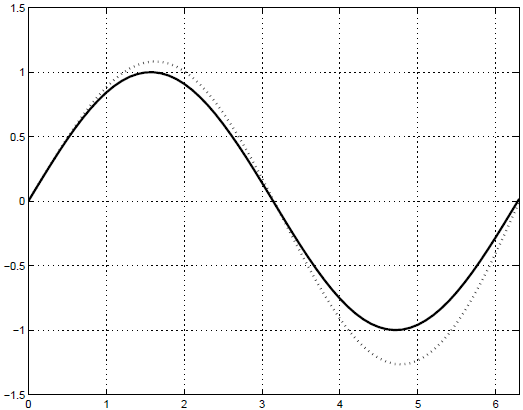
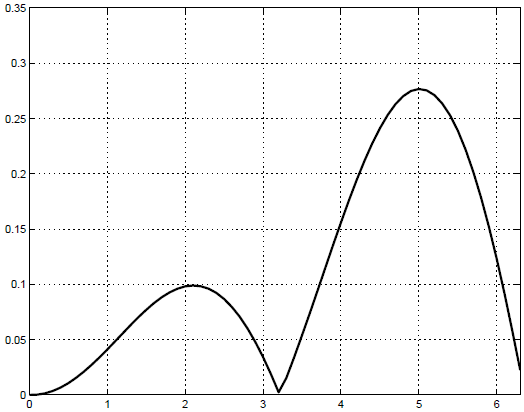
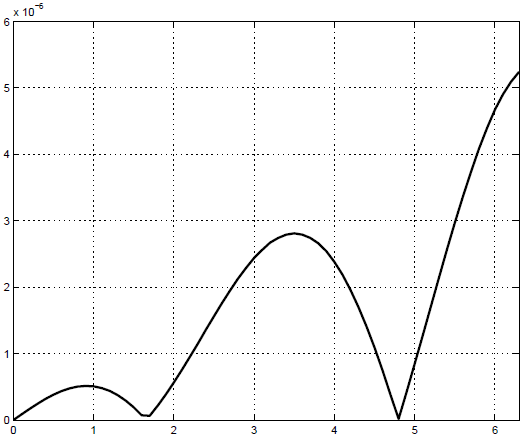
Результаты расчетов приведем на трех графиках. На рисунке 16.1 мы приводим график точного решения и приближенных, полученных методами Эйлера и Рунге-Кутты. Однако на этом графике не возможно отличить точное решение от приближенного решения, полученного методом Рунге-Кутты. На рисунках 16.2 и 16.3 мы показываем погрешности методов. Из анализа этих графиков видно, что точность метода Рунге-Кутты значительно выше, что обосновывается теоретически.
Ключевые термины
Глобальное решение - решение задачи Коши, существующее при
всех  .
.
Задача Коши - дифференциальное уравнение с заданными начальными условиями на решение.
Метод Рунге-Кутта - наиболее распространенный метод численного интегрирования задачи Коши с точностью четвертого порядка.
Метод Эйлера - простейший метод численного интегрирования задачи Коши с точностью первого порядка.
Условие Липшица - условие на приращение функции, более сильное чем условие непрерывности, но слабее чем условие дифференцируемости.
Краткие итоги: Построены объектно-ориентированные средства для численного решения задачи Коши. Проведены вычислительные эксперименты, для сравнения методов Эйлера и Рунге-Кутты.