Обыкновенные дифференциальные уравнения
Существует довольно много численных методов решения задачи Коши
для дифференциальных уравнений. При этом многие методы были
созданы еще в "до машинную эпоху". Такие методы часто
ориентированы на ручной расчет и включают в себя использование
аналитических выкладок, например, расчет производных от правой
части. Наиболее часто используемым является метод Рунге-Кутта.
Этот метод имеет весьма высокую точность, может иметь переменный
шаг и может быть легко запрограммирован. Одним из самых простейших
методов решения дифференциального уравнения является метод Эйлера.
Мы подробно рассмотрим метод Эйлера и метод Рунге-Кутта 
-го
порядка.
Метод Эйлера применялся еще Л.Эйлером для доказательства существования решения задачи Коши. Он имеет интуитивно понятную форму, легко может быть запрограммирован, но имеет низкую точность. И так, рассмотрим уравнение 16.1. Производную в этом уравнении приближенно представим с помощью конечной разности:
некоторое число. Используя это представление мы вместо
дифференциального уравнения 16.1 получим разностное
уравнение
 |
( 16.4) |
![[0,T]](/sites/default/files/tex_cache/b74093923941d33ee19becc5f4b48b25.png)
.
Разобьем этот отрезок конечным числом точек необязательно
равномерно
, 
. Для
простоты будем предполагать, что функция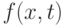 
определена во
всем пространстве 
. Тогда мы можем построить набор 
по следующему правилу
. Вектора 
имеют смысл
значений приближенного решения в точках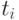 
. Для нахождения
приближенного решения внутри интервалов 
можно
применять различные методы интерполяции, например, линейной.
Функция 
, построенная с помощью линейной интерполяции,
называется ломанной Эйлера. Если для рассматриваемой задачи
выполнены условия теоремы 16.2 и на отрезке
существует решение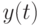 
, то приближенное решение
сходится к точному решению равномерно имеет место оценка![\max\limits_{t\in[0,T]}|y(t)-y^N(t)|\le Ch.](/sites/default/files/tex_cache/f9694031dcbff55903bd820afe34a99c.png)
Реализуем этот метод на C#. Сначала реализуем абстрактный класс, который будет использован для конструирования различных методов построения численных решений систем обыкновенных дифференциальных уравнений.
![\begin{verbatim}
abstract class TODE
{
public int N;
protected double t; // текущее время
// искомое решение Y[0] - само решение,
// Y[i] - i-тая производная решения
public double[] Y;
protected double[] YY; // внутренние переменные
public TODE(int N) // N - размерность системы
{
this.N = N;
Y = new double[N]; // создать вектор решения
YY = new double[N]; // и внутренних решений
}
// установить начальные условия.
// t0 - начальное время, Y0 - начальное условие
public void SetInit(double t0, double[] Y0)
{
t = t0;
int i;
for (i = 0; i < N; i++)
{
Y[i] = Y0[i];
}
}
public double GetCurrent() // вернуть текущее время
{
return t;
}
abstract public void F(double t, double[] Y,
ref double[] FY); // правые части системы.
// следующий шаг, dt - шаг по времени
abstract public void NextStep(double dt);
}
\end{verbatim}](/sites/default/files/tex_cache/bf8ee2b7ba152d5650669b93fb0e803c.png)
На основе этого класса построим класс, реализующий метод Эйлера.
![\begin{verbatim}
abstract class TEuler : TODE
{
public TEuler(int N) : base(N) {}
public override void NextStep(double dt)
{
int i;
F(t, Y, ref YY);
for (i = 0; i < N; i++)
{
Y[i] = Y[i] + dt * YY[i];
}
t = t + dt;
}
}
\end{verbatim}](/sites/default/files/tex_cache/79d97cd9415fdc8e45ebfb58e3721247.png)
Прежде чем испытать наш метод Эйлера, мы рассмотрим и реализуем
метод Рунге-Кутта -го порядка. Метод Рунге-Кутта, также как и
метод Эйлера, допускает перемену шага, но имеет значительно
большую точность. Пусть 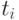и имеют тот же смысл, что и
при рассмотрении метода Эйлера.
Правила построения точек следующие
