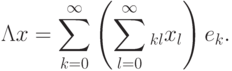Опубликован: 18.05.2011 | Доступ: свободный | Студентов: 976 / 106 | Оценка: 4.40 / 4.20 | Длительность: 12:30:00
Тема: Программирование
Специальности: Программист, Архитектор программного обеспечения
Теги:
Лекция 12:
О решении операторных уравнений
Лабораторная работа "Реализация операторов в гильбертовых пространствах"
Цель занятия
Продемонстрировать на характерных примерах реализацию линейных операторов в сепарабельных гильбертовых пространствах.
Сценарий лабораторной работы
- Напишите программу на языке C#, для вычисления произвольного оператора, заданного матрицей.
- Возьмите для примера функцию
 , постройте функцию после действия на нее матричного оператора и начертите график полученной функции.
, постройте функцию после действия на нее матричного оператора и начертите график полученной функции. - Проанализируйте каким образом действие этого оператора зависит от выбора базисных функций.
- Повторите эти опыты для различных матричных операторов и функций.
Указания
Матричный оператор в сепарабельном гильбертовом пространстве
вводится следующим образом. Пусть в рассматриваемом гильбертовом
пространстве  задан ортонормированный базис
задан ортонормированный базис  . Действие
матричного оператора
. Действие
матричного оператора  на некоторый элемент
на некоторый элемент