О решении операторных уравнений
Перейдем к программированию классов для реализации операторного подхода к решению задачи 11.1 - 11.2.




Теперь будем решать численно нашу задачу для разных значений  и
правых частей
и
правых частей  .
.

В итоге получим следующие результаты:

Сравним наши результаты с точными решениями при  . Задача
. Задача

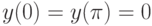

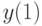 равно
равно

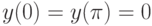

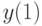 равно
равно

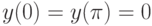

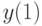 равно
равно
Ключевые термины
Гильбертово пространство  - наиболее известное
гильбертово функциональное пространство, состоящее из измеримых
функций, интегрируемых в квадратом модуля.
- наиболее известное
гильбертово функциональное пространство, состоящее из измеримых
функций, интегрируемых в квадратом модуля.
Краевая задача - дифференциальное уравнение с заданными условиями на решение на концах отрезка.
Метод Галеркина - общий метод для приближенного нахождения решений операторных уравнений.
Краткие итоги: Подробно рассмотрены методы численного решения краевой задачи для дифференциального уравнения второго порядка. С помощью реализованных классов, проведены различные вычислительные эксперименты.
