Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость
1.1 Постановка некоторых задач для уравнений математической физики
Напомним некоторые корректные постановки задач для уравнений в частных производных , которые будут встречаться в дальнейшем.
Задача Коши для уравнения теплопроводности.
Найти функцию u(t , x) в области ![x \in (- \infty , \infty), t \in [0, T]](/sites/default/files/tex_cache/01b35a4cc9a1bbaa4bd75f945f952839.png) , удовлетворяющую уравнению
, удовлетворяющую уравнению
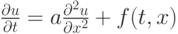
и начальным данным u(0, x) = u0(x), где u0(x) — заданная функция.
Смешанная задача для уравнения теплопроводности.
Найти функцию u(t , x) в области ![x \in [0, X], t \in [0, T]](/sites/default/files/tex_cache/62e3fbeac3f6ef0eff8cc12a8b308b5f.png) , удовлетворяющую уравнению
, удовлетворяющую уравнению

начальным данным u(0, x) = u0(x) и краевым условиям, записанным в общей форме
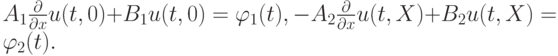
Смешанная задача для уравнения переноса.
Найти функцию u(t , x) в области ![x \in [0, X], t \in [0, T]](/sites/default/files/tex_cache/62e3fbeac3f6ef0eff8cc12a8b308b5f.png) , удовлетворяющую уравнению (для определенности положим c > 0 ):
, удовлетворяющую уравнению (для определенности положим c > 0 ):

начальным данным Коши
u(0, x) = u0(x), t = 0
и левому краевому условию
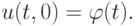
Смешанная задача для волнового уравнения.
Найти функцию u(t , x) в области ![x \in [0, X], t \in [0, T]](/sites/default/files/tex_cache/62e3fbeac3f6ef0eff8cc12a8b308b5f.png) , удовлетворяющую уравнению
, удовлетворяющую уравнению
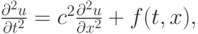
с начальными данными
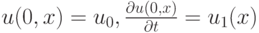
и краевыми условиями 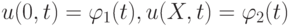 .
.
Эллиптическая краевая задача (уравнение Пуассона).
Найти функцию u(x , y) в области ![x \in [0, X], y \in [0, Y]](/sites/default/files/tex_cache/a802062ad4a7502ce4f4ff88463073b3.png) , удовлетворяющую уравнению
, удовлетворяющую уравнению
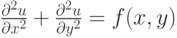
и краевым условиям 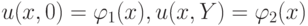 ,
, 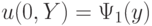 ,
,  .
.
Простейший способ построения численных решений для уравнений в частных производных — метод сеток. В дальнейшем, наряду с методом сеток, будем рассматривать и другие подходы к численному решению задач , например, вариационные, методы конечных элементов.
Рассмотрим постановку разностной задачи в методе сеток на примере одномерного уравнения теплопроводности.
Для решения одномерной смешанной задачи для уравнений в частных производных
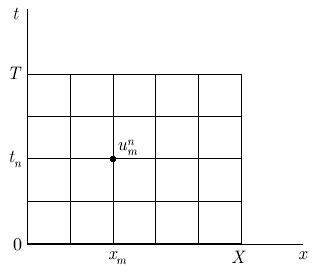
параболического типа область определения искомой функции покрывается расчетной сеткой с узлами в точках {tn, xm}, n = 0, ... , N, m = 0, ... , M ,  , xm = mh,
, xm = mh, 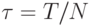 , h = X/M , где
, h = X/M , где 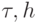 — шаги сетки по времени и пространству соответственно. Приближенным решением задачи назовем сеточную функцию
— шаги сетки по времени и пространству соответственно. Приближенным решением задачи назовем сеточную функцию  . Верхний индекс в такой форме записи сеточной функции традиционно указывает на номер слоя по времени, нижний (нижние) — на номер узла сетки по пространственной координате (рис. 1.1).
. Верхний индекс в такой форме записи сеточной функции традиционно указывает на номер слоя по времени, нижний (нижние) — на номер узла сетки по пространственной координате (рис. 1.1).
Рассмотрим подходы к построению численных алгоритмов для приближенного решения уравнений в частных производных.
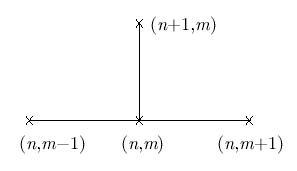
Явная разностная схема для приближенного решения уравнения теплопроводности во внутренних узлах сетки (не принадлежащим границе сеточной области) имеет вид
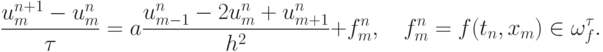
Под разностной схемой понимается совокупность разностных уравнений для определения значений сеточной функции внутри расчетной области, дополненная соответствующими начальными и граничными условиями для этой сеточной функции. Шаблон схемы, представляющий собой конфигурацию расчетных узлов в области интегрирования, используемых на каждом элементарном шаге вычислений , показан на рис. 1.2.
Эта схема аппроксимирует дифференциальное уравнение во внутренних точках (узлах) области интегрирования, т.е. при n = 1 , ... , N - 1, m = 1 , ... , M - 1. Проведем аппроксимацию начальных данных и краевых условий:
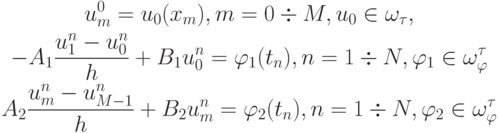
для определенности положим 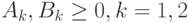 .
.
Расчет ведется по рекуррентной формуле на каждом временном слое от n = 1 до n = N от m = 1 до m = M - 1 во внутренних узлах; слой n = 0(t = t0) соответствует начальным данным, лучи m = 0(x = x0) и m = M(x = xM) — левому и правому краевым условиям.
Запишем явную схему в виде

По этой формуле последовательно, на каждом слое вычисляется сеточная функция во внутренних узлах области интегрирования.
Для завершения расчета слоя t = tn + 1 необходимо вычислить 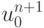 и
и 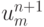 , для чего разрешаем левое и правое краевые условия относительно этих величин:
, для чего разрешаем левое и правое краевые условия относительно этих величин:
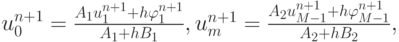
где 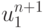 и
и 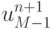 уже вычислены
ранее. Реализация одного шага по времени занимает O(M) арифметических операций , всех слоев — O(NM) операций.
уже вычислены
ранее. Реализация одного шага по времени занимает O(M) арифметических операций , всех слоев — O(NM) операций.
Явными схемами называются такие разностные схемы для эволюционных уравнений , когда данные на следующем слое по времени находятся непосредственно из данных на предыдущем слое без решения алгебраических систем уравнений. Если же на верхнем временном слое для определения значений сеточной функции необходимо решать систему алгебраических уравнений , то схема называется неявной.
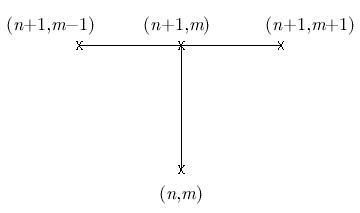
Простейшая неявная разностная схема имеет вид (для простоты положим a = 1 )
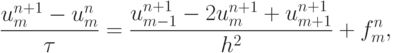
ее шаблон (рис. 1.3).
На каждом временном слое имеем СЛАУ с трехдиагональной матрицей; алгоритм ее решения — прогонка.
Неявную схему представим в виде
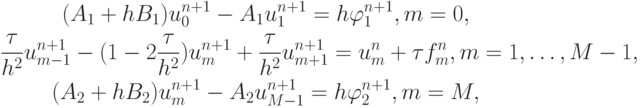
откуда несложно получить прогоночное соотношение на каждом слое по времени.