Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость
1.2 Основные определения — сходимость, аппроксимация, устойчивость
1.2.1. Основные определения.
Дадим основные определения из теории разностных схем.
Пусть 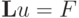 и
и  — операторные обозначения исходной дифференциальной и аппроксимирующей ее
разностной задачи (точнее, параметрического семейства задач);
— операторные обозначения исходной дифференциальной и аппроксимирующей ее
разностной задачи (точнее, параметрического семейства задач); 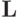 и
и 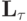 — соответственно, дифференциальный и разностный операторы,
— соответственно, дифференциальный и разностный операторы, 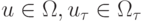 —
решения дифференциального и разностного уравнений , принадлежащие соответствующим функциональным пространствам,
—
решения дифференциального и разностного уравнений , принадлежащие соответствующим функциональным пространствам, 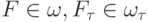 — правая часть исходного уравнения и ее проекция на
расчетную сетку. Считается известным способ получения проекции непрерывной функции на сетку. В простейшем случае используются значения функции, вычисленные в
узлах сетки. Индекс
— правая часть исходного уравнения и ее проекция на
расчетную сетку. Считается известным способ получения проекции непрерывной функции на сетку. В простейшем случае используются значения функции, вычисленные в
узлах сетки. Индекс  в этой операторной записи указывает на всю
совокупность сеточных параметров. Можно сказать, что для дискретной задачи имеется не один оператор, а совокупность различных операторов , зависящих от набора параметров.
в этой операторной записи указывает на всю
совокупность сеточных параметров. Можно сказать, что для дискретной задачи имеется не один оператор, а совокупность различных операторов , зависящих от набора параметров.
Например, задачу Коши для линейного одномерного уравнения переноса
![\begin{gather*}
\frac{du}{dt} - \frac{du}{dx} = f (t , x), t \in [0, T], x \in [0, X], \\
u (0, x) = {\varphi}(x),
\end{gather*}](/sites/default/files/tex_cache/3d158ca9488c6d9b9f926519d6dc4148.png)
можно представить в виде

Здесь
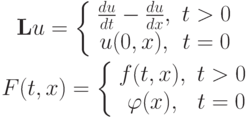
Одна из аппроксимирующих эту задачу разностных схем (правый уголок) имеет вид
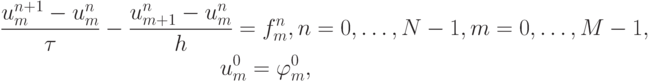
или в операторной форме
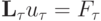
где
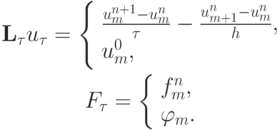
Определение 1. Говорят, что решение 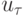 сходится к решению при
сходится к решению при  , если
, если 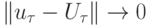 , где
, где  — проекция точного решения на разностную сетку; причем, если имеет место оценка
— проекция точного решения на разностную сетку; причем, если имеет место оценка  ,
, 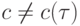 , то сходимость имеет порядок p.
, то сходимость имеет порядок p.
В качестве примера исследуем на сходимость разностную схему для задачи Коши для обыкновенного дифференциального уравнения (схема Эйлера)
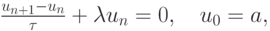
аппроксимирующую простейшее ОДУ
![$
\frac{du}{dt} + {\lambda}u = 0, t \in [0, 1], u(0) = a. $](/sites/default/files/tex_cache/bd9b186437c551a9c935baa32bab2d66.png)
Из разностного уравнения

найдем его общее решение:

Решение дифференциальной задачи легко находится: