Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость
Теорема. (об устойчивости по начальным данным для несамосопряженного оператора  (без доказательства))
(без доказательства))
Разностная схема
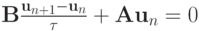
равномерно устойчива по начальным данным, если
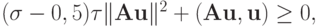
причем для ее решения справедлива оценка
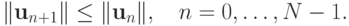
Таким образом, рассмотрен вопрос об устойчивости разностной схемы, записанной в операторной канонической форме
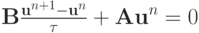 |
( 1.10) |
в случае 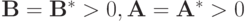 , причем
, причем  и
и 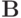 — постоянные матрицы. Рассмотрим более сложные случаи, в частности схему с весами
— постоянные матрицы. Рассмотрим более сложные случаи, в частности схему с весами
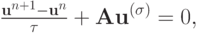 |
( 1.11) |
где  — кососимметрический оператор:
— кососимметрический оператор: 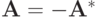 , тогда
, тогда  . Пример таких схем — простейшие разностные схемы для уравнения переноса:
. Пример таких схем — простейшие разностные схемы для уравнения переноса:
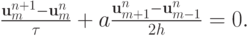
Представим разностную схему (1.11) в каноническом виде (1.10)

Заметим, что  . Кроме того,
. Кроме того,  верно
верно 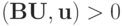 . Тогда
. Тогда  , и, сделав замену,
, и, сделав замену,  , имеем:
, имеем:
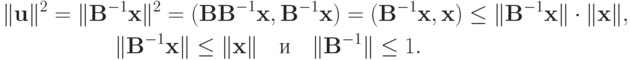
Схема (1.10) представима в виде
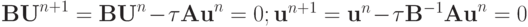
(разрешенный относительно верхнего временного слоя вид).
Найдем 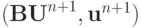 .
.
![\begin{gather*}
({\mathbf{BU}}^{n + 1} , {\mathbf{u}}^{n + 1} ) = ({\mathbf{BU}}^{n} -{\tau}{\mathbf{Au}}^{n}, {\mathbf{u}}^{n} -{\tau}{\mathbf{B}}^{- 1}{\mathbf{Au}}^{n}) = \\
= ({\mathbf{BU}}^{n}, {\mathbf{u}}^{n} ) -{\tau}[({\mathbf{Au}}^{n}, {\mathbf{u}}^{n}
) + ({\mathbf{BU}}^{n}, {\mathbf{B}}^{- 1}{\mathbf{Au}}^{n} )] +{\tau}^2 ({\mathbf{Au}}^{n}, {\mathbf{B}}^{- 1}{\mathbf{Au}}^{n} ). \end{gather*}](/sites/default/files/tex_cache/d95d9f8f8420fe8741123ab64165ba70.png)
В этом случае идеология доказательства оказывается похожей на доказательство устойчивости методов Рунге - Кутты на нейтральных по устойчивости траекториях. Первое слагаемое в квадратных скобках равно нулю, оценим второе слагаемое:
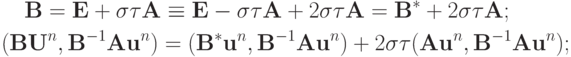
первое из слагаемых в левой части выражения — нуль. В результате имеем:
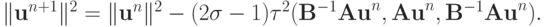 |
( 1.12) |
Если 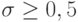 , то
, то 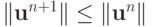 , и схема устойчива по начальным данным. Можно показать, что она также
будет устойчива и по правой части.
, и схема устойчива по начальным данным. Можно показать, что она также
будет устойчива и по правой части.
Пусть теперь 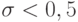 . Из (1.12) следует, что
. Из (1.12) следует, что
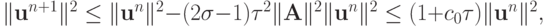
где 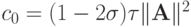 . Если
. Если 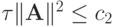 , то в случае
, то в случае 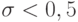 разностная схема будет равномерно устойчива с
разностная схема будет равномерно устойчива с  . Из устойчивости по начальным данным и в этом случае следует устойчивость по правой части.
. Из устойчивости по начальным данным и в этом случае следует устойчивость по правой части.
Рассмотрим пример: уравнение Шредингера движения частицы во внешнем поле ( m = 1 )
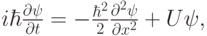
или, после обезразмеривания, получим

Если внешнего поля нет, можно потенциальную энергию частицы  положить равной нулю. На отрезке [0;1] можно записать разностную схему "с комплексными коэффициентами", аппроксимирующую уравнение
Шредингера:
положить равной нулю. На отрезке [0;1] можно записать разностную схему "с комплексными коэффициентами", аппроксимирующую уравнение
Шредингера:
 |
( 1.13) |
