Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы

Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость

A
|
версия для печати
Лекция 1: 1234567891011 || Лекция 2 >

Величина погрешности решения, входящая в определение сходимости, тогда будет 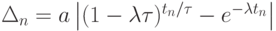\Delta_n = a \left| {(1 - {\lambda}{\tau})^{t_n /{\tau}} - e^{- {\lambda}t_n }}\right|.

Представим 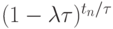(1 - {\lambda}{\tau})^{t_n /{\tau}} в виде

\begin{gather*} (1 - {\lambda}{\tau})^{t_n /{\tau}} = \exp (\frac{{t_n }}{\tau} \ln (1 - {\lambda}{\tau})) = \exp \frac{{t_n }}{\tau} \left[{- {\lambda}{\tau}+ \frac{{{\lambda}^2{\tau}^2}}{2} + O({\tau}^3 )}\right] = \\ = e^{- {\lambda}t_n } \left[{1 + \frac{{{\lambda}^2{\tau}t_n }}{2} + O({\tau}^2 )}\right] \left[{1 + O({\tau}^2 )}\right] = e^{- {\lambda}t_n } + \frac{\tau}{2} {\lambda}^2 t_n e^{- {\lambda}t_n } + O({\tau}^2 ). \end{gather*}

Тогда

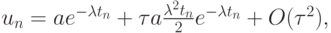
$ u_n = ae^{- {\lambda}t_n } +{\tau}a \frac{{{\lambda}^2 t_n }}{2}e^{- {\lambda}t_n } + O({\tau}^2 ), $

и, следовательно,

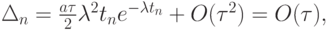
$ \Delta_n = \frac{{a{\tau}}}{2} {\lambda}^2 t_n e^{- {\lambda}t_n } + O({\tau}^2 ) = O({\tau}), $

т.е. разностная схема имеет первый порядок сходимости. К сожалению, чтобы исследовать схему на сходимость, необходимо знать точное решение дифференциальной задачи. Обычно разностные схемы исследуются на аппроксимацию и устойчивость, откуда по теореме П.Лакса и В.С.Рябенького и следует сходимость, по крайней мере, для линейных задач.

Пример разностной задачи, аппроксимирующей рассматриваемое уравнение:

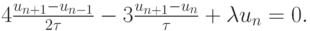
$ 4 \frac{{u_{n + 1} - u_{n - 1}}}{{2{\tau}}} - 3 \frac{{u_{n + 1} - u_n}}{\tau} + {\lambda}u_n = 0. $

Можно показать, получив общее решение разностной задачи, что эта схема не является устойчивой и, следовательно, не имеет место сходимость решения к точному решению дифференциальной задачи.

Определение 2. Говорят, что разностная задача аппроксимирует дифференциальную на ее решении, если норма невязки, возникающей при действии разностного оператора на сеточную функцию — проекцию на сетку точного решения

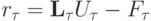
r_{\tau} = {\mathbf{L}}_{\tau}U_{\tau} - F_{\tau}

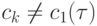стремится к нулю при {\tau}\to 0; если выполнена оценка \left\| {r_{\tau}}\right\| \le c_k{\tau}^{p}, {c_k \ne c_1 ({\tau})} (константа, входящая в правую часть неравенства, не зависит от сеточных параметров), то имеет место аппроксимация порядка p.

Приведем пример исследования разностной схемы на аппроксимацию, для чего напомним следующие соотношения, полученные с помощью разложения проекции точного решения на сетку в ряд Тейлора в окрестности одного из сеточных узлов:

\begin{gather*} U(t +{\tau}) = U(t) +{\tau}U^{\prime}_t (t) + \frac{{{\tau}^2}}{{2!}}U^{\prime\prime}_t (t) + \frac{\tau^3}{3!}U_t^{(3)} (t) + \frac{\tau^4}{4!}U_t^{(4)} (t) + O({\tau}^5 ) \\ U^{\prime}(t) \approx \frac{U(t +{\tau}) - U({\tau})}{\tau} = U^{\prime}(t) + \frac{\tau}{2}U^{\prime\prime}_t (t) + O({\tau}^2 ), \\ U^{\prime}(t) \approx \frac{{U(t) - U(t -{\tau})}}{\tau} = U^{\prime}(t) - \frac{\tau}{2}U^{\prime\prime}_t + O({\tau}^2 ), \\ U^{\prime}(t) \approx \frac{U(t +{\tau}) - U(t -{\tau})}{2 \tau} = U^{\prime}(t) + \frac{\tau^2}{3}U_t^{(3)} (t) + O({\tau}^3 ), \\ U(t -{\tau}) = U(t) -{\tau}U^{\prime}_t ({\tau}) + \frac{\tau^2}{2!}U^{\prime\prime}_t ({\tau}) - \frac{\tau^3 }{3!}U_t^{(3)} (t) + \frac{\tau^4 }{4!}U_t^{(4)} + O({\tau}^5 ); \\ U^{\prime\prime}(t) \approx \frac{U(t +{\tau}) - 2U(t) + U(t -{\tau})}{\tau^2} = U^{\prime\prime}(t) + \frac{\tau^2}{12}U_t^{(4)} (t) + O({\tau}^4 ). \end{gather*}

Рассмотрим задачу Коши для уравнения переноса

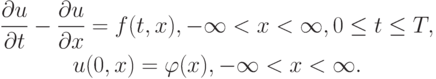
\begin{gather*} \frac{{\partial}u}{{\partial}t} - \frac{{\partial}u}{{\partial}x} = f(t , x), - \infty < x < \infty , 0 \le t \le T , \\ u(0, x) = {\varphi}(x), - \infty < x < \infty. \end{gather*}

Введем разностную сетку и положим

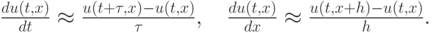
$ \frac{du(t , x)}{dt} \approx \frac{u(t +{\tau}, x) - u (t , x)}{\tau}, \quad \frac{du(t , x)}{dx} \approx \frac{u(t , x + h) - u (t , x)}{h}. $

Получим введенную выше схему "правый уголок".

Положив , что функция u(t , x) имеет ограниченные вторые производные, получим выражения для главных членов погрешности аппроксимации, т.е. тех членов , которые определяются минимальными степенями сеточных параметров.

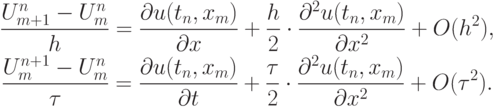
\begin{gather*} \frac{U_{m + 1}^n - U_m^n}{h} = \frac{{\partial}u(t_n , x_m )}{{\partial}x} + \frac{h}{2} \cdot \frac{\partial^2 u(t_n , x_m )}{{\partial}x^2} + O(h^2 ), \\ \frac{U_m^{n + 1} - U_m^n}{\tau} = \frac{{\partial}u(t_n , x_m )}{{\partial}t} + \frac{\tau}{2} \cdot \frac{\partial^2 u(t_n , x_m )}{{\partial}x^2} + O({\tau}^2 ). \end{gather*}

Тогда для невязки верно равенство 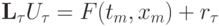{\mathbf{L}}_{\tau} U_{\tau} = F(t_m , x_m ) + r_{\tau}, или, так как в силу самого дифференциального уравнения

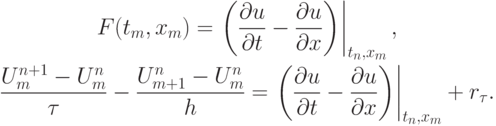
\begin{gather*} F(t_m , x_m ) = \left. {\left({\frac{{\partial}u}{{\partial}t} - \frac{{\partial}u}{{\partial}x}}\right)} \right|_{t_n , x_m }, \\ \frac{{U_m^{n + 1} - U_m^{n}}}{\tau} - \frac{{U_{m + 1}^{n} - U_m^{n}}}{h} = \left. {\left({\frac{{\partial}u}{{\partial}t} - \frac{{\partial}u}{{\partial}x}}\right)}\right|_{t_n , x_m } + r_{\tau} . \end{gather*}

Здесь невязка 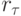r_{\tau } определяется выражением

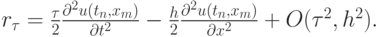
$ r_{\tau} = \frac{\tau}{2} \frac{\partial^2 u(t_n , x_m )}{{\partial}t^2} - \frac{h}{2} \frac{{\partial}^2 u(t_n , x_m )}{{\partial}x^2} + O({\tau}^2 , h^2 ). $

Так как 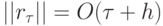|| r_{\tau } || = O(\tau + h), то разностная схема имеет первый порядок аппроксимации по \tau и h.

Дальше >>
Лекция 1: 1234567891011 || Лекция 2 >

Вопросы и ответы

вопросов: 0