Понятие о методах конечных элементов
Основная идея метода конечных элементов, базирующаяся на методах Бубнова, Галеркина и Ритца, была предложена Р.Курантом в 1943 г., но осталась незамеченной, опередив потребности практики. В 50 - х годах прошлого века с появлением первых компьютеров возникла необходимость в разработке новых инженерных подходов к численному решению задач со сложной геометрией, в которых области интегрирования разбивались на подобласти. Такие подобласти ( носители финитных базисных функций, об этом ниже) и получили название конечных элементов.
Методы конечных элементов (МКЭ) в настоящее время, пожалуй, самые распространенные в мире численные методы. К их достоинствам относятся:
- возможность счета на неравномерных сетках, в двумерном и трехмерном случаях для областей сложной геометрии;
- "технологичность" методов (уточнение далее).
Современные МКЭ возникли в 50 - е годы XX века при решении задач теории упругости.
Самая распространенная статическая задача — задача о нагруженной конструкции
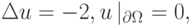
а область  — сложная. Например, область может иметь
вид, представленный на рис. 7.1. Каждая простая подобласть — конечный элемент.
— сложная. Например, область может иметь
вид, представленный на рис. 7.1. Каждая простая подобласть — конечный элемент.
В настоящее время под МКЭ понимают целые семейства вариационных ( Ритца ) и проекционных ( Галеркина или Бубнова - Галеркина ) методов.
7.1. Вариационный подход Ритца
Рассмотрим две задачи:
 |
( 7.1) |
 |
( 7.2) |
Эти задачи похожи: (7.1) является одномерным случаем более общей задачи (7.2). Уравнения (7.1) и (7.2) записаны в самосопряженной форме. Поставим задачам (7.1) и (7.2) в соответствие функционалы
 |
( 7.3) |
и
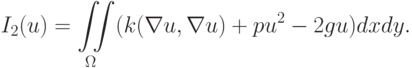 |
( 7.4) |
Будем рассматривать пространство функций  (пространство Соболева) с нормой
(пространство Соболева) с нормой
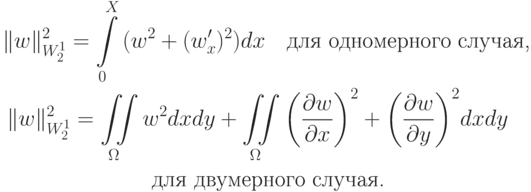
Это — функции с ограниченным интегралом.
Теорема 5. Среди всех функций  , удовлетворяющих граничным условиям, решение задачи (7.1) придает наименьшее значение функционалу (7.3), а решение (7.2) — функционалу (7.4).
, удовлетворяющих граничным условиям, решение задачи (7.1) придает наименьшее значение функционалу (7.3), а решение (7.2) — функционалу (7.4).
Доказательство.
Докажем это утверждение для одномерного случая, а доказательство для уравнений (7.2), (7.4) оставим в качестве упражнений.
Введем 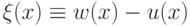 . Поскольку
. Поскольку  , а u(x) — дважды непрерывно дифференцируемая функция, то
, а u(x) — дважды непрерывно дифференцируемая функция, то  и
и  .
.
 |
( 7.5) |
Третье слагаемое в (7.5) равно нулю в силу граничных условий для функции  ; последнее слагаемое равно нулю, так как u — решение (7.1); второе слагаемое — неотрицательное. Следовательно, минимум функционала I1(w) достигается, когда
; последнее слагаемое равно нулю, так как u — решение (7.1); второе слагаемое — неотрицательное. Следовательно, минимум функционала I1(w) достигается, когда 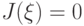 , т. е.
, т. е.  или, что то же самое, w(x) = u(x) .
или, что то же самое, w(x) = u(x) .
Чуть сложнее эта теорема доказывается для двумерного случая, где надо воспользоваться теоремой Остроградского - Гаусса. Таким образом, решение соответствующей задачи в частных производных (7.2) или краевой задачи для ОДУ (7.1) сводится к задаче минимизации некоторого функционала.
В том случае, если функционал (7.3) или (7.4) ограничен снизу, то экстремаль функционала — минимум, и численный метод, который будет построен ниже, носит название метода Ритца. Чаще, когда нет необходимости тщательно исследовать постановку задачи, говорят об экстремальной точке, стационарной точке функционала и т.д.

