НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 7: Понятие о методах конечных элементов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1275 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

7.6. МКЭ для нестационарных уравнений

Рассмотрим простейшую МКЭ - аппроксимацию уравнения теплопроводности:

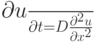
$\frac{{\partial}u}{{\partial}t} = D \frac{{{\partial}^2 u}}{{{\partial}x^2}}$

с соответствующими граничными и начальными условиями. Будем искать решение в виде

$u = \sum\limits_{j = 1}^{N}{C_j (t) \psi_j^{N}}.$

Используя подход Галеркина, получаем (в базисе из "крышечек")

$\frac{1}{6} \frac{{dC_{j - 1}}}{dt} + \frac{2}{3} \frac{{dC_j }}{dt} + \frac{1}{6} \frac{{dC_{j + 1}}}{dt} = \frac{D}{{h^2}}(C_{j - 1} - 2C_j + C_{j + 1}).$

Это — система дифференциально - разностных уравнений. Теперь необходимо заменить производные по времени разностными отношениями.

Заметим, что "явная" схема (когда в правой части стоят коэффициенты разложения на предыдущем слое по времени 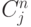$C_j^{n}$ ) уже не является явной, в соответствии с определением явных методов, данном выше:

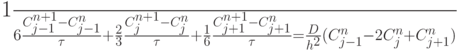
$\frac{1}{6} \frac{{C_{j - 1}^{n + 1} - C_{j - 1}^{n}}}{\tau} + \frac{2}{3} \frac{{C_j^{n + 1} - C_j^{n}}}{\tau} + \frac{1}{6} \frac{{C_{j + 1}^{n + 1} - C_{j + 1}^{n}}}{\tau} = \frac{D}{{h^2}}(C_{j - 1}^{n} - 2C_j^{n} + C_{j + 1}^{n} )$

и на n + 1 - м слое все равно необходимо решать систему уравнений методом прогонки. Причиной этого вычислительного неудобства является то, что система дифференциальных уравнений для определения зависимости коэффициентов разложения — это система обыкновенных дифференциальных уравнений, но не записанная в нормальной форме Коши.

Попытаемся исследовать схему на устойчивость спектральному признаку фон Неймана. Подставив в приведенное выше разностное уравнение

$C_j^{n} = {\lambda}^{n}e^{ij {\varphi}},$

получаем выражение для спектра оператора послойного перехода $\lambda(\varphi):$

$\frac{{{\lambda} - 1}}{6}[e^{i {\varphi}} + 4 + e^{- i {\varphi}} ] = k[e^{i {\varphi}} + 2 + e^{- i {\varphi}}],$

где

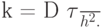
$k = D \frac{\tau}{h^2}.$

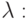
Отсюда видно, что устойчивость метода конечных элементов опять определяется безразмерной комбинацией параметров разбиения (размера конечного элемента, шага по времени) и коэффициента теплопроводности — параболическим аналогом числа Куранта. Преобразуем уравнение для $\lambda:$

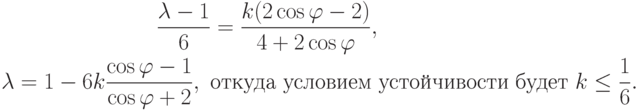
$\begin{gather*} \frac{{\lambda}- 1}{6} = \frac{{k(2 \cos {\varphi}- 2)}}{{4 + 2 \cos {\varphi}}}, \\ {\lambda} = 1 - 6k \frac{{\cos {\varphi} - 1}}{{\cos {\varphi}+ 2}}, \mbox{ откуда условием устойчивости будет } k \le \frac{1}{6}. \end{gather*}$

Имеет смысл пользоваться "неявной схемой" (правая часть берется с верхнего слоя по времени) или аппроксимацией типа Кранка - Никольсон.

Продолжим рассмотрение применения МКЭ к нестационарным уравнениям. Как и ранее, смотрим задачу для уравнения теплопроводности

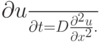
$\frac{{\partial}u}{{\partial}t} = D \frac{{{\partial}^2 u}} {{{\partial}x^2}}.$

Выбирая базис из "крышечек", представляем решение в виде

$u = \sum\limits_{j = 1}^{N}{C_j (t) \psi_j^{N}}.$

Подставляя последнее уравнение в исходное и применяя стандартную процедуру метода Галеркина, получаем систему дифференциальных уравнений

$\frac{1}{6} \frac{{dC_{j - 1}}}{dt} + \frac{2}{3} \frac{{dC_j }}{dt} + \frac{1}{6} \frac{{dC_{j + 1}}}{dt} = \frac{D}{{h^2}}(C_{j - 1} - 2C_j + C_{j + 1})$

(шаг сетки считается постоянным), или, в матричном виде

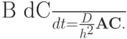${{\mathbf{B}} \frac{d{\mathbf{C}}}{dt} = \frac{D}{{h^2}}{\mathbf{AC}}.}$

( 7.15)

При этом, в любом базисе

${\mathbf{B}} = {\mathbf{B}}^* > 0, \quad {\mathbf{A}} = {\mathbf{A}}^* > 0.$

Тогда

$\exists {\mathbf{B}}^{1/2} : \quad {\mathbf{B}}^{1/2}{\mathbf{B}}^{1/2} = {\mathbf{B}}.$

Матрица ${\mathbf{B}}^{1/2}$ - самосопряженная положительно определенная. Можно записать последнее уравнение (7.15) в виде

${\mathbf{B}}^{1/2}{\mathbf{B}}^{1/2} \frac{{d{\mathbf{C}}}}{dt} = \frac{D}{{h^2}}{\mathbf{AB}}^{- 1/2}{\mathbf{B}}^{1/2}{\mathbf{C}}.$

Введем вектор 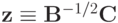${\mathbf{z}} \equiv {\mathbf{B}}^{- 1/2}{\mathbf{C}}$ и умножим последнее соотношение слева на 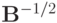${\mathbf{B}}^{- 1/2}$ , тогда получаем

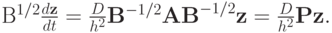${{\mathbf{B}}^{1/2} \frac{{d{\mathbf{z}}}}{dt} = \frac{D}{{h^2}}{\mathbf{B}}^{- 1/2}{\mathbf{AB}}^{- 1/2}{\mathbf{z}} = \frac{D}{{h^2}}{\mathbf{P}}{\mathbf{z}}.}$

( 7.16)

Таким образом, из неявной системы (7.15) получена "явная" система (7.16) — перед вектором производных нет матричного множителя.

Запишем для (7.16) схему Кранка - Николсон:

${{\mathbf{z}}^{n + 1} - {\mathbf{z}}^{n} = \frac{{D {\tau}}}{{2h^2}}{\mathbf{B}}^{- 1/2}{\mathbf{AB}}^{- 1/2} ({\mathbf{z}}^{n + 1} + {\mathbf{z}}^{n}).}$

( 7.17)

Вопрос об устойчивости схемы (7.17) можно решить следующим образом. Умножим (7.17) на ${\mathbf{z}}^{n + 1} + {\mathbf{z}}^{n}$ . Получаем соотношение:

$\begin{gather*} ({\mathbf{z}}^{n + 1}, {\mathbf{z}}^{n + 1}) - ({\mathbf{z}}^{n}, {\mathbf{z}}^{n}) = \frac{{\sigma}}{2}({\mathbf{B}}^{- 1/2} {\mathbf{AB}}^{- 1/2} ({\mathbf{z}}^{n + 1} + {\mathbf{z}}^{n}), ({\mathbf{z}}^{n + 1} + {\mathbf{z}}^{n}));\\ \|{\mathbf{z}}^{n + 1}\|^2 = \|{\mathbf{z}}^{n}\|^2 + \frac{{\sigma}}{2}({\mathbf{P}}({\mathbf{z}}^{n + 1} + {\mathbf{z}}^{n}), ({\mathbf{z}}^{n + 1} + {\mathbf{z}}^{n})) \le \|{\mathbf{z}}^{n}\|^2 - \frac{{{\sigma}{\lambda}}}{2} \|{\mathbf{z}}^{n + 1} + {\mathbf{z}}^{n}\|^2 \end{gather*}$

в силу того, что 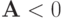${\mathbf{A}} < 0$ (спектр оператора ${\mathbf{A}}$ уже известен). Последнее неравенство и означает безусловную устойчивость метода.

Дальше >>

Авторизоваться

Численные методы решения уравнений в частных производных

Понятие о методах конечных элементов

7.6. МКЭ для нестационарных уравнений

Вопросы и ответы