Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)
3.1. Простейшее линейное уравнение переноса
Рассмотрим простейший пример уравнений в частных производных. Пусть в некотором объеме движущейся жидкости находится пассивная примесь, т.е. такая, наличие которой не меняет принципиально характер движения. Например, это может быть маркер — краска, чернила или мелкие частицы, которые специально добавлены в жидкость для визуализации течений. Тогда изменение концентрации примеси в любом сколь угодно малом объеме равно потоку примеси через границы объема в единицу времени (закон сохранения массы), и можно записать, устремляя рассматриваемый объем к нулю
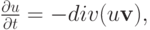
где u — концентрация пассивной примеси,  — скорость течения жидкости. Пусть жидкость
несжимаема и
— скорость течения жидкости. Пусть жидкость
несжимаема и
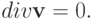
Тогда из двух предыдущих соотношений сразу следует уравнение
 |
( 3.1) |
Равенство (3.1) будем в дальнейшем называть уравнением переноса пассивной примеси или линейным уравнением переноса. Кроме (3.1), будем рассматривать и одномерное уравнение переноса
 |
( 3.2) |
а также неоднородное уравнение переноса
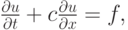 |
( 3.3) |
где f — заданная функция, играющая роль источника (стока).
Неоднородным уравнением переноса описываются системы, в которых пассивная примесь может вступать, например, в химические реакции. Если уравнения переноса описывают распространение планктона, то в правой части будет стоять функция, описывающая размножение планктона и его пассивную утечку (например, за счет его поедания рыбами). О неоднородных линейных моделях речь пойдет ниже.
Уравнения вида (3.1), (3.2), (3.3) традиционно рассматриваются в курсах обыкновенных дифференциальных уравнений [13.1], [13.2].
Причина этого кроется в следующем обстоятельстве. Рассмотрим систему ОДУ
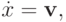 |
( 3.4) |
соответствующую (3.1). Это — уравнение характеристик для линейного уравнения переноса. Если функция u является первым интегралом (3.4), то она является решением (3.1). Иными словами, вдоль характеристики решение однородного уравнения переноса сохраняет постоянное значение.
Упражнение. Найти в явном виде уравнение характеристики для (3.2). В какое уравнение перейдет неоднородное уравнение переноса (3.3) вдоль характеристики?
Для корректной постановки задач для линейного уравнения переноса начальные и граничные условия необходимо ставить на некоторой гиперповерхности. Так как решение уравнений переноса распространяется вдоль характеристик, то начальная гиперповерхность должна быть трансверсальной ко всем характеристикам (не иметь точек касания с характеристиками ). Кроме того, если для однородного уравнения переноса какая - либо характеристика имеет с начальной гиперповерхностью более одной общей точки, то значения начальной функции во всех этих точках должны быть равны между собой. Все эти условия достаточно очевидны, если вспомнить физический смысл уравнения переноса.
Отметим, что наличие характеристик можно считать условием того, что система имеет гиперболический тип. Так, если система уравнений произвольного порядка n имеет n действительных характеристик, будем называть ее гиперболической. Таким образом, линейное уравнение переноса имеет гиперболический тип.
