Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 3:

Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)
A
|
версия для печати
< Лекция 2 || Лекция 3: 1234567891011 || Лекция 4 >

3.5. Методы регуляризации численных решений с большими градиентами

Кроме основных понятий теории разностных схем — аппроксимации, устойчивости, сходимости — на практике существенную роль играют дополнительные свойства разностных схем. Среди таких свойств упомянем монотонность. Не существует общепринятого определения монотонности разностной схемы. Пока, до рассмотрения разностных схем в пространстве неопределенных коэффициентов, воспользуемся определением, данным Борисом и Буком в [13.5], [13.6].

Под монотонными далее будем понимать такие разностные схемы, в которых не увеличивается число локальных экстремумов (минимумов и максимумов численного решения) по сравнению с числом локальных экстремумов в решении точной задачи. Кроме того, монотонные схемы не должны увеличивать по абсолютному значению уже имеющиеся экстремумы.

Свойство монотонности разностной схемы очень полезно при расчете разрывных решений. К сожалению, доказанная для линейного уравнения переноса теорема С.К.Годунова гласит, что среди линейных разностных схем (термин "линейный" уточним чуть ниже) не существует монотонных с порядком аппроксимации выше первого.

Зачастую в практических задачах схемы первого порядка аппроксимации не могут обеспечить требуемую точность численного решения.

При использовании немонотонных схем для получения численных решений с большими градиентами, появляются осцилляции разностного происхождения. По этой причине в численных методах часто используется регуляризация численных решений. Рассмотрим наиболее распространенные методы регуляризации.

Сглаживание численного решения на верхнем слое (метод Л.А.Чудова) .

Вычисленное с помощью немонотонной разностной схемы значение функции в точке xn корректируется следующим образом:

$ \tilde{u}_m = (1 - 2{\alpha})u_m +{\alpha} u_{m - 1} + {\alpha} u_{m + 1}, $

причем при 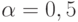{\alpha} = 0, 5 значение 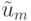\tilde{u}_m является средним арифметическим

$ \tilde{u}_n = 0, 5(u_{m - 1} + u_{m + 1}) . $

Для того чтобы понять действие сглаживающего оператора, представим явную схему для численного решения линейного одномерного уравнения теплопроводности

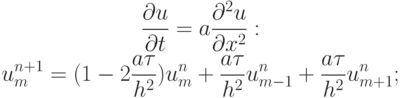
\begin{gather*} \frac{{\partial}u}{{\partial}t} = a \frac{{{\partial}^2 u}}{{{\partial}x^2}}: \\ u_m^{n + 1} = (1 - 2 \frac{{a{\tau}}}{{h^2}})u_m^{n} + \frac{{a{\tau}}}{{h^2}}u_{m - 1}^{n} + \frac{{a{\tau}}}{{h^2}}u_{m + 1}^{n} ; \end{gather*}

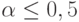т.е. при {\alpha} = {a{\tau}/{h^2}} сглаживание аппроксимирует диссипативный член, пропорциональный второй производной по координате. Понятно, что скорректированное решение будет устойчивым при {\alpha} \le 0, 5. Для снятия этого ограничения можно ввести алгоритм неявного сглаживания. Он имеет вид

$ \tilde{u}_m = (1 - 2{\alpha}) \tilde{u}_m + {\alpha} \tilde{u}_{m - 1} +{\alpha} \tilde{u}_{m + 1}. $

Подробнее о сглаживании по Л.А.Чудову можно прочитать, например, в [13.7].

Аппроксимационная вязкость.

Рассмотрим схему первого порядка аппроксимации, для численного решения модельного однородного уравнения переноса (3.3)

$ \mathbf{L}_{\tau} u^{\tau} = \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + c \frac{{u_m^{n} - u_{m - 1}^{n}}}{h} = 0, $

исследование которой на аппроксимацию дает следующее выражение для главных членов ошибки аппроксимации (главных членов невязки):

\begin{gather*} \mathbf{L}_{\tau} u^{\tau} = \mathbf{L}u + \frac{\tau}{2} \cdot \frac{{{\partial}^2 u}} {{{\partial}t^2}} - \frac{{ch}}{2} \cdot \frac{{{\partial}^2 u}}{{{\partial}x^2}} + O({\tau}^2 + h^2 ) = \\ = \mathbf{L}u - \frac{{ch}}{h}(1 - \frac{{c \tau}}{2}) \frac{{{\partial}^2 u}} {{{\partial}x^2}} + O({\tau}^2 + h^2 ) \end{gather*}

Таким образом, с точностью до членов второго порядка, аппроксимируется уравнение

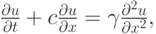
$ \frac{{\partial}u}{{\partial}t} + c \frac{{\partial}u}{{\partial}x} = \gamma \frac{{{\partial}^2 u}}{{{\partial}x^2}}, $

где аналог коэффициента теплопроводности

$ \gamma = \frac{{ch}}{2}(1 - \frac{{c \tau}}{h}) $
— так называемый коэффициент аппроксимационной вязкости, а член

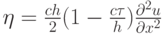
$ \eta = \frac{{ch}}{2}(1 - \frac{{c{\tau}}}{h}) \frac{{{\partial}^2 u}} {{{\partial}x^2}} $

именуется аппроксимационной вязкостью. Его действие — сглаживание численного решения. Слагаемые в правой части уравнения переноса, пропорциональные второй производной, моделируют диссипативный эффект. Однако эта вязкость является свойством выбранной разностной схемы первого порядка аппроксимации. Здесь в уравнение не вводятся никакие дополнительные члены и не используются сглаживающие операторы. Рассматриваемое уравнение носит название первого дифференциального приближения разностной схемы. Все схемы первого порядка аппроксимации будут обладать схемной вязкостью.

Упражнения. Некоторая разностная схема для решения уравнения переноса (3.3) первого порядка аппроксимации обладает отрицательным коэффициентом схемной вязкости. Что можно сказать о других свойствах этой схемы (устойчивость, сходимость, монотонность)?

Искусственная вязкость.

Для регуляризации решения, полученного с помощью немонотонных разностных схем с порядком аппроксимации выше первого можно вводить так называемую искусственную вязкость. Этот способ регуляризации решения был предложен фон Нейманом и Рихтмайером для численного решения системы уравнений газовой динамики. В рамках данной лекции ограничимся рассмотрением модельного линейного уравнения переноса.

Идею искусственной вязкости можно проиллюстрировать на примере, вообще говоря, неустойчивой схемы

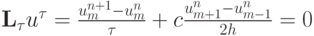
$ \mathbf{L}_{\tau} u^{\tau} = \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + c \frac{{u_{{m} + 1}^{n} - u_{m - 1}^{n}}}{2h} = 0 $

для решения линейного одномерного уравнения переноса (3.3).

Для того чтобы сделать эту схему устойчивой, введем в правую часть член порядка погрешности аппроксимации, моделирующий диссипативный эффект, так называемую искусственную вязкость. Получим следующую задачу:

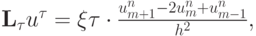
$ \mathbf{L}_{\tau} u^{\tau} = \xi{\tau} \cdot \frac{{u_{{m} + 1}^{n} - 2u_m^{n} + u_{m - 1}^{n}}}{{h^2}}, $

где

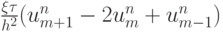
$ \frac{\xi{\tau}}{h^2}(u_{m + 1}^{n} - 2u_m^{n} + u_{m - 1}^{n}) $
— искусственная вязкость, величина порядка главного члена погрешности аппроксимации (невязки) \xi — коэффициент искусственной вязкости. Исследование этой схемы на устойчивость с помощью спектрального признака дает
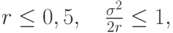
$ r \le 0, 5, \quad \frac{{{\sigma}^2}}{{2r}} \le 1, $
где
$ r = \frac{{\xi{\tau}}}{{h^2}}, \quad {\sigma}= \frac{c{\tau}}{h} $
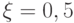. При \xi = 0, 5 для рассматриваемого линейного уравнения получим схему Лакса - Вендроффа.

Упражнения. Построить четырехточечную схему с искусственной вязкостью для квазилинейного уравнения (уравнения Хопфа в форме (3.5) и в форме {3.6)).

Методы коррекции потоков Бориса - Бука.

Рассмотрим идею введения схемной антидиффузии, предложенную Борисом и Буком в [13.5], [13.6]. Пусть 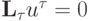\mathbf{L}_{\tau} u^{\tau} = 0 — схема первого порядка точности, аппроксимирующая линейное одномерное уравнение переноса (13.3) и обладающая аппроксимационной вязкостью.

Уменьшим влияние последней на численное решение, введя так называемые потоки антидиффузии (терминология авторов метода):

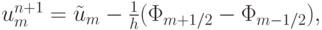
$ u_m^{n + 1} = \tilde{u}_m - \frac{1}{h}(\Phi_{{m} + 1/2} - \Phi_{{m} - 1/2}), $

где 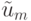$ \tilde{u}_m $ — решение, полученное по упомянутой схеме, \Phi_{m \pm 1/2} — потоки, имеющие вид

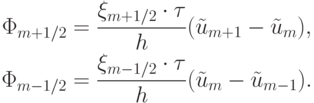
\begin{gather*} \Phi_{{m} + 1/2} = \frac{{\xi_{{m} + 1/2} \cdot{\tau}}}{h}(\tilde{u}_{{m} + 1} - \tilde{u}_m ), \\ \Phi_{m - 1/2} = \frac{{\xi_{m - 1/2} \cdot{\tau}}}{h}(\tilde{u}_m - \tilde{u}_{m - 1}). \end{gather*}

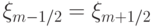При \xi _{m - 1/2} = \xi _{m + 1/2} разностное уравнение имеет вид

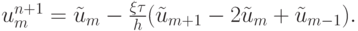
$ u_m^{n + 1} = \tilde{u}_m - \frac{{\xi{\tau}}}{h}(\tilde{u}_{m + 1} - 2 \tilde{u}_m + \tilde{u}_{m - 1}). $

Таким образом, идея метода коррекции потоков состоит во введении сглаживающего оператора определенного вида. Метод коррекции потоков описан, например, в [13.5].

Дальше >>
< Лекция 2 || Лекция 3: 1234567891011 || Лекция 4 >

Вопросы и ответы

вопросов: 0