Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)
3.2. Квазилинейные уравнения гиперболического типа. Характеристики квазилинейных уравнений
Рассмотрим теперь более сложные примеры уравнений первого порядка в частных производных. Уравнение вида
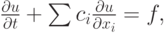 |
( 3.5) |
где f = f(t, xi, u), ck = ck (t, xi, u), будем называть квазилинейным уравнением (переноса) [13.1], [13.2]. Естественно предположить, что все функции, входящие в запись (3.5), достаточно гладкие (подробнее в [13.1]. Для квазилинейных уравнений также существует понятие характеристики. В соответствии с [13.1], [13.2], уравнения характеристик для (3.5) будут иметь вид
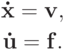
Последние соотношения для характеристик легко переписываются в координатах:
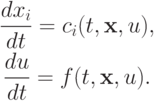
Рассмотрим пример нахождения характеристик для квазилинейного уравнения.
Уравнения газовой динамики моделируются уравнением Хопфа:

Для вывода уравнения Хопфа рассмотрим одномерную среду, состоящую из частиц, которые движутся по инерции. Считаем, что движение происходит вдоль прямой. Запишем для частиц второй закон Ньютона:
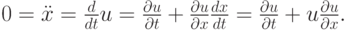
Найдем характеристики уравнения Хопфа:
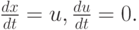
Отметим, что линейное уравнение можно рассматривать как частный случай квазилинейного уравнения. При этом можно ввести определение характеристики для линейного уравнения аналогично характеристике для квазилинейного уравнения. Заметим, что характеристика квазилинейного уравнения, вообще говоря, определяется в пространстве более высокой размерности, чем для линейного уравнения. Характеристики линейного уравнения, определенные выше, в этом случае совпадают с проекциями на гиперплоскость (x1, ..., xn) характеристик квазилинейного уравнения. В частном случае для однородных квазилинейных уравнений можно рассматривать характеристики на гиперплоскости (x1, ..., xn). Тогда характеристики уравнения Хопфа можно считать прямыми линиями x(t) = x(0) + u(x(0), 0)t. На практике при построении численных методов часто именно эти линии и считаются характеристиками уравнения Хопфа.
Используя метод характеристик, можно решать уравнения Хопфа. Рассмотрим в качестве примера уравнение Хопфа с начальным условием u(x, 0) = ch- 2(x). Построим характеристики для данной задачи, пользуясь начальными данными. Вдоль каждой характеристики значение функции остается постоянным. Можно построить решение вплоть до момента времени, когда характеристики начинают пересекаться. После этого решение уравнения Хопфа в классическом смысле перестает существовать. Далее существует лишь разрывное обобщенное решение типа ударной волны. На разрыве (фронте ударной волны), вообще говоря, необходимо ставить дополнительные условия. Пересечение характеристик и образование ударной волны в решении также называют градиентной катастрофой. Более подробная информация о свойствах уравнения Хопфа в [13.3]. Конечно, возможно найти численное решение уравнения Хопфа в виде ударной волны. Речь об этом пойдет ниже.
3.3. Численные методы решения уравнений в частных производных гиперболического типа на примере линейного уравнения переноса
Двухслойные разностные схемы. Линейное одномерное уравнение переноса, как отмечалось выше, имеет вид (3.3)
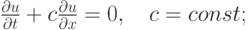
Наряду с линейным уравнением переноса, в следующем параграфе будем рассматривать также квазилинейные уравнения. Простейшее квазилинейное уравнение гиперболического типа — уравнение Хопфа (3.5). Оно интересно тем, что моделирует уравнения газовой динамики. Запишем его в двух формах:
 |
( 3.6) |
( дивергентная форма ). Отметим, что дивергентная форма записи отражает наличие некоторого закона сохранения. В случае уравнения Хопфа это закон сохранения импульса. В другой форме,
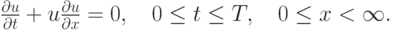 |
( 3.7) |
Эту форму записи иногда в дальнейшем будем называть характеристической. Отметим, что для линейных уравнений с постоянными коэффициентами нет принципиальной разницы между характеристической и дивергентной формами. Для уравнений с переменными коэффициентами эта разница возникает даже в линейном случае. При использовании различных форм записи для построения разностных схем возникают численные методы с разными свойствами.
Для корректной постановки начальной и краевой задач необходимо корректно задать начальные и граничные условия. Они для рассматриваемых ниже задач имеют вид
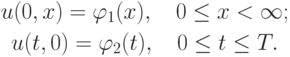
Для определенности пока положим c > 0.
Решением задачи Коши для уравнения (3.3) является "бегущая волна":

где c — скорость переноса, а функция 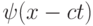 определяется из начальных или граничных условий. Характеристики уравнения имеют вид x - ct = const и при постоянной скорости переноса являются прямыми линиями. Решение однородного уравнения (3.3), как отмечено выше, остается постоянным вдоль характеристики, поэтому начальные и граничные условия переносятся вдоль этих линий. В случае неоднородного уравнения вдоль характеристики оно превращается в обыкновенное дифференциальное уравнение.
определяется из начальных или граничных условий. Характеристики уравнения имеют вид x - ct = const и при постоянной скорости переноса являются прямыми линиями. Решение однородного уравнения (3.3), как отмечено выше, остается постоянным вдоль характеристики, поэтому начальные и граничные условия переносятся вдоль этих линий. В случае неоднородного уравнения вдоль характеристики оно превращается в обыкновенное дифференциальное уравнение.
Приведем вид двухпараметрического семейства двухслойных разностных схем первого и второго порядков точности [13.4]:
 |
( 3.8) |
где применены обозначения
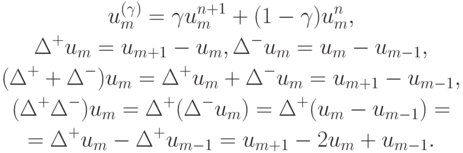
Рассмотрим теперь конкретные разностные схемы решения модельного линейного уравнения переноса .
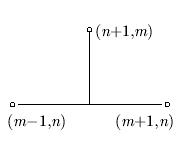
Схема П. Лакса (трехточечная схема) получается при 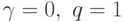 . Ее порядок аппроксимации
. Ее порядок аппроксимации 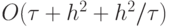 . Здесь и далее порядок аппроксимации приводится для модельного уравнения переноса с постоянными коэффициентами. В случае переменных коэффициентов в схему надо внести необходимые изменения. При этом естественно линейное уравнение рассматривать как
частный случай квазилинейного.
. Здесь и далее порядок аппроксимации приводится для модельного уравнения переноса с постоянными коэффициентами. В случае переменных коэффициентов в схему надо внести необходимые изменения. При этом естественно линейное уравнение рассматривать как
частный случай квазилинейного.
Схема является условно устойчивой, т.е. при выполнении условия Куранта 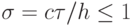 . Отметим здесь, что величина
. Отметим здесь, что величина  играет определяющую роль при исследовании разностных схем на аппроксимацию и устойчивость. Она называется числом Куранта. Исследование разностной схемы на устойчивость для линейного эволюционного
уравнения с постоянными коэффициентами можно провести с использованием спектрального признака (фон Неймана).
играет определяющую роль при исследовании разностных схем на аппроксимацию и устойчивость. Она называется числом Куранта. Исследование разностной схемы на устойчивость для линейного эволюционного
уравнения с постоянными коэффициентами можно провести с использованием спектрального признака (фон Неймана).