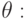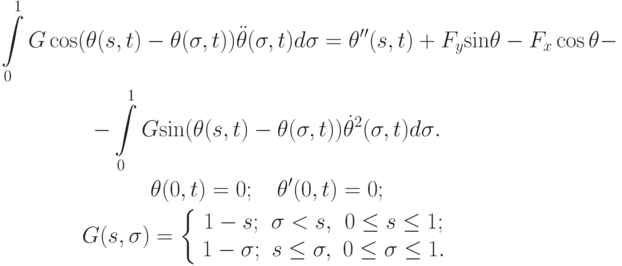Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 9:

Применение вариационных принципов для построения разностных схем
A
|
версия для печати
< Лекция 8 || Лекция 9: 123456 || Дополнительный материал  >
Аннотация: В необязательной лекции приводятся примеры использования вариационных принципов Лагранжа и Гамильтона для построения разностных схем на основе вариации дискретного аналога лагранжиана (гамильтониана) системы. В Приложении на примере решения конкретной задачи по проектированию установки рассмотрены основные схемы распараллеливания численных методов
Ключевые слова: метод Галеркина, консервативные разностные схемы, энергия, коэффициенты, вариационные принципы Лагранжа и Гамильтона, дифференциальное уравнение, функция, отрезок, метод трапеций, погрешность, ПО, равенство, выражение, алгебраические системы, матрица, аппроксимация, вторая производная, невязка, минимум, вариация, производные, конечные, разностная схема на неравномерной сетке, явная разностная схема, уравнения газовой динамики, линейное уравнение, прямоугольник, поток, координаты, площадь, поиск, проекция, внешняя нормаль, вес, значение, итерационные методы

Вариационный принцип Ритца, позволяющий получить МКЭ для уравнений в частных производных эллиптического типа, в том числе и на нерегулярных сетках, рассматривался в "Понятие о методах конечных элементов" . Далее для решения нестационарных задач в основном использовался проекционный вариант МКЭ (метод Галеркина). Тем не менее, многие задачи математической физики допускают вариационную постановку. Некоторые величины и законы сохранения могут играть особую роль для задач (пример — закон сохранения гамильтониана для консервативной системы). Необходимы разностные схемы (или численные методы), позволяющие учитывать специфику задачи и вариационные постановки.

Сделать это можно двумя способами. Первый — использовать вариационные принципы для дискретных аналогов соответствующих функционалов. При этом обычно получаются консервативные схемы. Второй способ — построение разностных схем обычными методами (конечных разностей), а затем их модификация, направленная на минимизацию погрешности аппроксимации законов сохранения.

Рассмотрим первый (вариационный) подход.

9.1. Пример использования принципа наименьшего действия (Гамильтона)

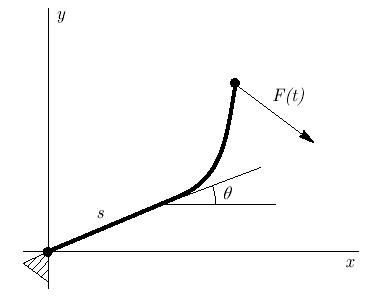
Рассматривается задача о движении твердого нерастяжимого стержня длиной 1. Пусть он закреплен в точке 0, а на другой конец стержня действует сила 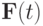{\mathbf{F}}(t) (рис. 9.1). Требуется определить движение стержня. Начальная форма стержня считается заданной.


Рис. 9.1.

Возможное решение: записать уравнение движения — получится уравнение гиперболического типа; поставить граничные условия; построить разностную схему. Но в задаче допускаются сколь угодно большие колебания стержня.

Другой способ приближенного решения. Введем \theta — угол отклонения от оси x — как функцию длины дуги s, времени t. Тогда имеем

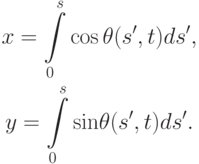
\begin{gather*} x = \int\limits_0^{s}{\cos \theta (s^{\prime}, t)ds^{\prime}}, \\ y = \int\limits_0^{s}{{\sin}\theta (s^{\prime}, t)ds^{\prime}}. \end{gather*}

Кинетическая энергия стержня есть

$ T = \int\limits_0^1 {\left({\frac{{V_x^2}}{2} + \frac{{V_y^2}}{2}}\right)ds} = \frac{1}{2} \int\limits_0^1 {\left({\left[{\frac{{\partial}x}{{\partial}t}}\right]^2 + \left[{\frac{{\partial}y}{{\partial}t}}\right]^2}\right)ds}, $

а потенциальная энергия складывается из упругой энергии (изгиба) и работы внешней силы 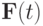{\mathbf{F}}(t):

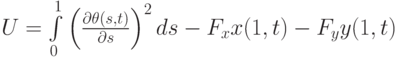
$ U = \int\limits_0^1 {\left({\frac{{{\partial}\theta (s, t)}} {{{\partial}s}}}\right)^2 ds} - F_x x(1, t) - F_y y(1, t) $

(соответствующие коэффициенты полагаются равными 1 ).

Лагранжиан системы есть L = T - U, так что

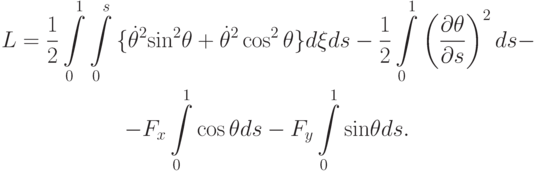
\begin{gather*} L = \frac{1}{2} \int\limits_0^1 {\int\limits_0^{s}{\{\dot \theta ^2 {\sin}^2 \theta + \dot \theta ^2 \cos ^2 \theta \} d \xi } ds} - \frac{1}{2} \int\limits_0^1 {\left({\frac{{{\partial}\theta }}{{{\partial}s}}}\right)^2 ds} - \\ - F_x \int\limits_0^1 {\cos \theta ds} - F_y \int\limits_0^1 {{\sin}\theta ds} . \end{gather*}

Согласно принципу Гамильтона, функционал действия достигает экстремального значения на истинном движении. Отсюда следует, что

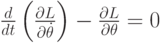
$ \frac{d}{dt} \left({\frac{{{\partial}L}}{{{\partial}\dot \theta }}} \right) - \frac{{{\partial}L}}{{{\partial}\theta }} = 0 $

и получается уравнение движения для \theta:

\begin{gather*} \int\limits_0^1 {G \cos (\theta (s, t) - \theta ({\sigma}, t)) \ddot \theta ({\sigma}, t)d {\sigma}} = {\theta}^{\prime\prime}(s, t) + F_y {\sin}\theta - F_x \cos \theta - \\ - \int\limits_0^1 {G {\sin}(\theta (s, t) - \theta ({\sigma}, t)) \dot \theta ^2 ({\sigma}, t)d {\sigma}} . \\ \theta (0, t) = 0; \quad \theta^{\prime}(0, t) = 0; \\ G(s, {\sigma}) = \left\{ \begin{array}{ccc} {1 - s;} & {{\sigma} < s, } & {0 \le s \le 1;} \\ {1 - {\sigma};} & {s \le {\sigma}, } & {0 \le {\sigma}\le 1.} \\ \end{array} \right. \end{gather*}
Дальше >>
< Лекция 8 || Лекция 9: 123456 || Дополнительный материал  >

Вопросы и ответы

вопросов: 0