Применение вариационных принципов для построения разностных схем
9.2. Вариационные схемы для решения задач газовой динамики
Более интересные разностные схемы получаются для многомерных задач. Особенно плодотворным вариационный подход оказывается при решении задач механики сплошной среды.
Рассмотрим следующий пример. В бесконечном объеме (вакууме) находится область  занятая газом (см. рис. 9.3). Масса газа
занятая газом (см. рис. 9.3). Масса газа 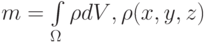 — плотность среды.
— плотность среды.
Движение системы подчиняется следующим уравнениям:
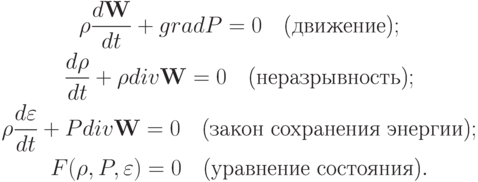
Эти уравнения приведены в лагранжевых переменных. Напомним, что полная производная определена как
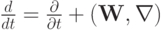
 обозначена скорость движения среды,
а через V — элемент объема. Рассматривается случай невязкого нетеплопроводного газа. Запишем лагранжиан для движения среды, представив ее как систему частиц, а затем устремим число частиц в бесконечность.
обозначена скорость движения среды,
а через V — элемент объема. Рассматривается случай невязкого нетеплопроводного газа. Запишем лагранжиан для движения среды, представив ее как систему частиц, а затем устремим число частиц в бесконечность.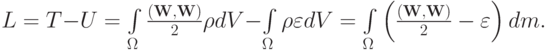
Движение среды должно доставлять минимум функционалу действия
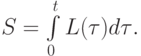
По закону сохранения массы 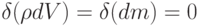 .
Найдем
.
Найдем 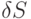 - вариацию S:
- вариацию S:
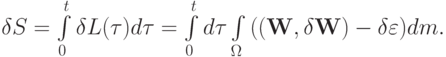
Согласно первому началу термодинамики в предположении адиабатичности процесса,
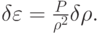
Используя кинематическое соотношение

получим, что
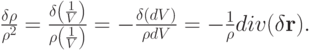
Тогда
![\begin{gather*}
\delta S = - \int\limits_0^{t}{d {\tau}} \int\limits_\Omega {\left({\rho \frac{{d{\mathbf{W}}}}{dt} + {grad}{P}}\right) \delta {\mathbf{r}}dV} + \\
+ \left. {\left[{\int\limits_\Omega {({\mathbf{W}}, \delta {\mathbf{r}}) \rho dV}}\right]}
\right|_0^{t} + \int\limits_0^{t}{d\tau} \oint\oint\limits_{\partial\Omega }{(\delta {\mathbf{r}}, {\mathbf{n}})Pd {\sigma}} = 0. \end{gather*}](/sites/default/files/tex_cache/4d916e2764a424d1b121fcb52eccaa4d.png)
Независимые вариации траекторий 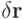 полагают равными нулю при
полагают равными нулю при 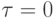 и
и 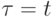 . Считая также
. Считая также  , получим, что вариация лагранжиана равна нулю на решении системы уравнений Эйлера газовой динамики.
, получим, что вариация лагранжиана равна нулю на решении системы уравнений Эйлера газовой динамики.
Рассмотрим дискретный аналог функционала действия. Для этого введем в  сетку с ячейками, пронумерованными по левому нижнему углу. При отображении
сетку с ячейками, пронумерованными по левому нижнему углу. При отображении  на квадрат сетка отображается на равномерную квадратную сетку (см. рис. 9.4). Тогда
на квадрат сетка отображается на равномерную квадратную сетку (см. рис. 9.4). Тогда
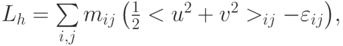
где 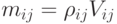 — масса ячейки (
— масса ячейки ( 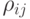 — ее плотность) < u2 + v2 > — усредненная по ячейке плотность кинетической энергии
— ее плотность) < u2 + v2 > — усредненная по ячейке плотность кинетической энергии
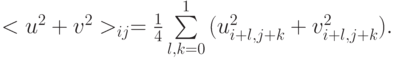
Условие адиабатичности течения имеет следствием для дискретной системы
выражение  .
.
Кинематические соотношения (уравнения движения для узлов сетки) есть
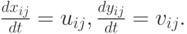
Объем каждой ячейки вычисляется в предположении, что границы ячейки — отрезки прямых:
![$ V_{ij} = \frac{1}{2}[(x_{i + 1j} - x_{ij + 1})(y_{i + 1j + 1} - y_{ij} ) - (x_{i + 1j + 1} - x_{ij} )(y_{i + 1j} - y_{ij + 1} )]. $](/sites/default/files/tex_cache/2b13d07438b5f3dab2283eb1205a4f56.png)
Теперь необходимо получить соответствующую систему дифференциально - разностных соотношений, аппроксимирующих уравнения Эйлера.
Запишем функционал действия
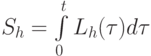
и найдем его вариацию:
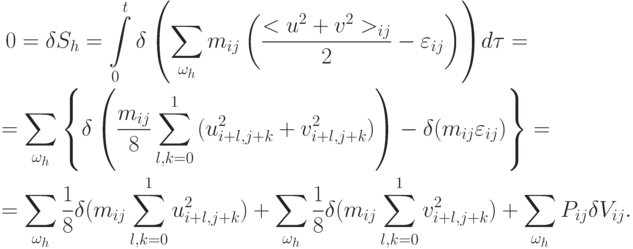
Первое слагаемое в последнем равенстве можно переписать как
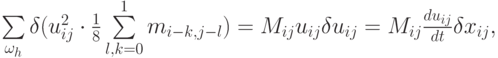
где
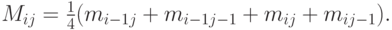
После преобразований получаются следующие соотношения:
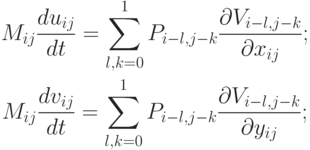
т.е. возникает система дифференциально - разностных уравнений движения.
Уравнение адиабатичности трактуется, как уравнение для определения энергии:
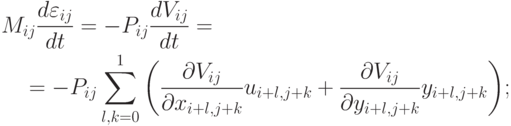
Система дифференциально - разностных соотношений замыкается уравнением состояния.
Теперь, заменяя производные по времени на конечные разности, получим разностную схему для решения уравнений газовой динамики на нерегулярной подвижной сетке. Обычно для решения таких уравнений используются явные разностные схемы. Подробнее о вариационных методах получения схем для уравнений газовой динамики в [19.2].