НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 9: Применение вариационных принципов для построения разностных схем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Имеем интегро - дифференциальное уравнение для определения $\theta (s, t)$ , причем как строить его разностную аппроксимацию — непонятно.

Отметим, что $G(s, \sigma )$ есть функция Грина для задачи

w'' = - g(s),     w'(0) = w(1) = 0.

Рис. 9.2.

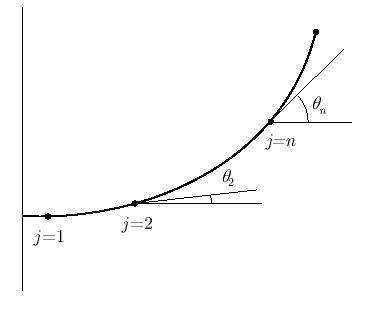
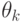Теперь введем дискретный аналог лагранжиана L_h. Для этого разобьем стержень на n отрезков одинаковой длины $\Delta l$ (и одинаковой массы). Каждый отрезок характеризуется углом наклона $\theta _{k}$ . Тогда (см. рис. 9.2)

$\begin{gather*} x_j = \sum\limits_{k = 1}^{j}{\Delta l \cos \theta_k } = \Delta l \sum\limits_{k = 1}^{j}{\cos \theta_k } ; \\ y_j = \Delta l \sum\limits_{k = 1}^{j}{{\sin}\theta_k } ; \\ T_{h} = \frac{\Delta l}{2} \sum\limits_{j = 1}^{n}{\dot{x} + \dot{y}} = \frac{(\Delta l)^3}{2} \sum\limits_{j = 1}^{n}{\frac{{\partial}z_j}{{\partial}t} \frac{{\partial}\bar{z}_j}{{\partial}t}};z_j = e^{i \theta_j } ; \\ U_{h} = \frac{\Delta l}{2} \sum\limits_{j = 2}^{n} \left(\frac{\theta_j - \theta_{j - 1}}{\Delta l}\right)^2 - F_x \Delta l \sum\limits_{j = 1}^{n}{\cos {\theta_j}} - F_y \Delta l \sum\limits_{j = 1}^{n}{\sin{\theta_j}}. \end{gather*}$

Здесь появился аналог конечных элементов или схем с центральными разностями. Интегралы в этом выражении заменены конечными изломами, фактически эти интегралы вычислены методом трапеций, т.е. погрешность в определении лагранжиана L_h есть 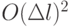$O(\Delta l)^{2}$ .

Теперь для построения системы уравнений надо записать

$\frac{d}{dt} \left({\frac{{{\partial}L_{h}}}{{{\partial}\dot \theta_m }}}\right) - \frac{{{\partial}L_{h}}}{{{\partial}\theta_m }} = 0, m = 1, 2, \ldots , n$

т. е. продифференцировать дискретный аналог функционала по всем значениям $\theta_m , \dot \theta_m$ на введенной сетке. Для рассматриваемой задачи последнее равенство приводит к соотношению

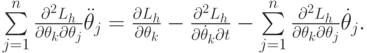
$\sum\limits_{j = 1}^{n}{\frac{{{\partial}^2 L_{h}}} {{{\partial}\theta_k {\partial}\theta_j }} \ddot \theta_j } = \frac{{{\partial}L_{h}}}{{{\partial}\theta_k }} - \frac{{{\partial}^2 L_{h}}}{{{\partial}\dot \theta_k {\partial}t}} - \sum\limits_{j = 1}^{n}{\frac{{{\partial}^2 L_{h}}} {{{\partial}\theta_k {\partial}\theta_j }} \dot \theta_j } .$

После подстановки в последнее выражение дискретного аналога лагранжиана и выполнения дифференцирования по всем $\theta_k , \dot {\theta}_k$ , получаем:

$\begin{gather*} \sum\limits_{k = 1}^{n}{\alpha_{lk} \ddot {\theta}_k } = n^4 (\theta_{l - 1} - 2 \theta_{l} + \theta_{l + 1} ) + \\ + n^2 (F_y \cos \theta_{l} - F_x {\sin}\theta_{l} ) - \sum\limits_{k = 1}^{n}{g_{lk} {\sin}(\theta_{l} - \theta_k ) \dot {\theta}_k ^2}. \end{gather*}$

(известно, что 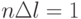$n\Delta l = 1$ по построению).

Таким образом, при использовании сеточного аналога вариационного принципа Гамильтона получена дифференциально - разностная система уравнений (дифференциальная по времени, разностная по пространственным переменным).

Рис. 9.3.

Несколько затруднительно решать эту систему как систему обыкновенных дифференциальных уравнений, так как она не приведена к нормальной форме Коши. Однако с последней дифференциально - алгебраической системой можно работать и решать ее. Алгоритмы решения основаны на том, что g_lk — сеточный аналог функции Грина. Обратная матрица — сеточная аппроксимация оператора второй производной. Подробное изложение метода решения в [19.1].

Дальше >>

Авторизоваться

Численные методы решения уравнений в частных производных

Применение вариационных принципов для построения разностных схем

Вопросы и ответы