НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 9: Применение вариационных принципов для построения разностных схем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

9.4. Задачи для самостоятельного решения

Уравнение Кортевега - Де Фриза
Одно из самых замечательных уравнений математической физики — уравнение Кортевега - Де Фриза (сокращенно КДФ) часто записывают в виде
```
u_t - 6uu_x + u_xxx = 0
```
или
- Найти преобразование, переводящее эти формы записи друг в друга.
- Рассматриваем задачу для уравнения u_t - 6uu_x + u_xxx = 0 в области $x \in [- 10;10]$ с условием периодичности.
  Для решения иногда используют трехслойную разностную схему на шаблоне рис. 9.8 (третья производная расписывается по пяти точкам симметричным образом, некоторые коэффициенты могут обратиться в нуль). Исследовать ее на аппроксимацию и устойчивость. Какое условие устойчивости получено? Построить разностную схему на шаблоне, напоминающем шаблон схемы Саульева для решения уравнения теплопроводности (рис. 9.9 а, б).
  
  Рис. 9.8.
  
  Рис. 9.9.
  
  Исследовать получившиеся схемы на аппроксимацию и устойчивость. Можно ли использовать прогонку для вычислений на верхнем слое?
- Уравнение u_t - 6uu_x + u_xxx = 0 имеет бесконечное число законов сохранения. Укажем несколько из них:
  $\begin{gather*} \int {udx = {const}_{1} , } \\ \int {u^2 dx = {const}_{2}} \\ \int {\left({\frac{{(u^{\prime}_{x})^2}}{2} + u^3 }\right)} dx = {const}_{3} = I_1 . \end{gather*}$
  
  Как построить консервативную разностную схему, чтобы на сеточном уровне выполнялись законы сохранения $\int {udx} = {const}{?}$
- Особую роль играет третий из приведенных выше законов сохранения. Он является гамильтонианом для уравнения u_t - 6uu_x + u_xxx = 0, т.е.
  $\frac{{\partial}u}{{\partial}t} = \frac{d}{dx} \left({\frac{{\delta I_1}}{{\delta u}}}\right).$
  
  Здесь
  $\frac{\delta I_1}{\delta u}$
  вариационная производная функционала I₁, способ получения разностной схемы, сохраняющей гамильтониан системы.
  
  Решение. Запишем сеточный аналог гамильтониана I₁:
  
  $I_{{1}}^{{h}} = \sum\limits_{m = - \infty }^{+ \infty } {\left[{\frac{1}{2} \left({\frac{{u_{{{m}} + {{1}}} - u_{{m}}}}{h}}\right)^2 + (u_{{m}} )^3 }\right]h = I_1 + O(h^2 )}.$
  
  Контрольный вопрос: почему $I_1^{h}$ аппроксимирует I₁ с точностью O(h²)?
  
  На сеточном уровне взятие вариационной производной означает дифференцирование по всем 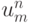$u_{m}^{n}$ и деление на h. Тогда получаем сеточную запись вариационной производной:
  
  $\begin{gather*} \frac{\delta I_1^h}{\delta u} = \frac{1}{h}\frac{{\partial}_1^h}{{\partial}u_m } = u_m^2 + \frac{1}{h^2}((u_m - u_{m - 1}) - (u_{m + 1} - u_m )) = \\ = 3u_m^2 - \frac{u_{m + 1} - 2u_{m} + u_{m - 1}}{h^2} + O(h^2). \end{gather*}$
  
  Аппроксимируя дискретный аналог (4.4.3) с естественным для этого вторым порядком по h, получаем
  
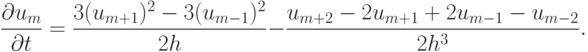
  $\frac{{\partial} u_m}{{\partial} t} = \frac{3(u_{m + 1})^2 - 3(u_{m - 1})^2}{2h} - \frac{u_{m + 2} - 2u_{m + 1} + 2u_{m - 1} - u_{m - 2}}{2h^3} .$
  
  Заменяя производную по времени разностью
  $\frac{u_m^{n + 1} - u_m^{n - 1}}{2 {\tau}}$
  и вычисляя правую часть на n слое, получаем одну из схем пункта 2.
  
  Конечно, возможны и другие аппроксимации гамильтониана, варьирование которых приводит к другим разностным схемам. Все они будут записываться на симметричных шаблонах, на сеточном уровне для этих схем также будет выполняться закон сохранения $\int {udx = {const}}$ .
  
  Удастся ли получить вариационную схему на несимметричном шаблоне типа Саульева?