Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы

Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость

A
|
версия для печати
Лекция 1: 1234567891011 || Лекция 2 >

1.5. Задачи для самостоятельного решения

  1. Для задачи Коши для линейного уравнения переноса

    $ \frac{{\partial}u}{{\partial}t} + a \frac{{\partial}u}{{\partial}x} = 0, $

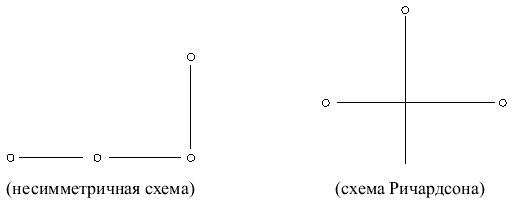
    построить разностные схемы и исследовать их на сходимость, используя шаблоны:


    Рис. 1.5.

    Разностная схема, построенная на симметричном трехточечном шаблоне, называется схемой П.Лакса.

  2. Для линейного уравнения теплопроводности

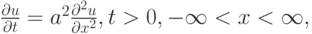
    $ \frac{{\partial}u}{{\partial}t} = a^2 \frac{{\partial}^2 u}{{\partial}x^2}, t > 0, - \infty < x < \infty , $

    построить разностные схемы и исследовать их на сходимость, используя шаблоны:


    Рис. 1.6.
  3. Построить разностные схемы для линейного волнового уравнения

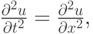
    $ \frac{{\partial}^2 u}{{\partial}t^2} = \frac{{\partial}^2 u}{{\partial}x^2}, $

    и исследовать их на сходимость, используя шаблоны


    Рис. 1.7.
  4. Построить разностную схему, сходящуюся к решению акустической системы

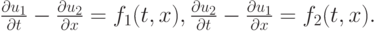
    $ \frac{{\partial}u_1}{{\partial}t} - \frac{{\partial}u_2}{{\partial}x} = f_1 (t , x), \frac{{\partial}u_2}{{\partial}t} - \frac{{\partial}u_1}{{\partial}x} = f_2 (t , x). $

  5. Построить разностную схему П. Лакса, аппроксимирующую задачу Коши для линейного двумерного уравнения переноса

    $ \frac{{\partial}u}{{\partial}t} - \frac{{\partial}u}{{\partial}x} - \frac{{\partial}u}{{\partial}y} = 0, $

    и исследовать ее на сходимость.

Дальше >>
Лекция 1: 1234567891011 || Лекция 2 >

Вопросы и ответы

вопросов: 0