Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость
По доказанной ранее теореме, данная схема устойчива по начальным данным в 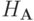 в
случае, если
в
случае, если

Тогда, в энергетической норме, порождаемой оператором  , схема Кранка - Николсон безусловно устойчива.
, схема Кранка - Николсон безусловно устойчива.
Схема с весами. Можно действовать также, как и для схемы Кранка - Николсон , а можно несколько иначе. Для общей записи схемы с весами
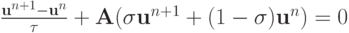
иногда употребляется сокращенная форма
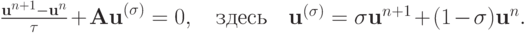
Умножив это разностное уравнение на 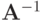 слева, получаем:
слева, получаем:
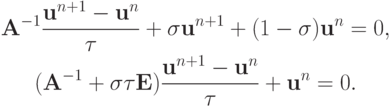
Тогда необходимое и достаточное условие устойчивости в норме, порождаемой оператором 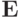 (т.е. в евклидовой норме)
(т.е. в евклидовой норме)

Так как  , домножим обе части
последнего неравенства на
, домножим обе части
последнего неравенства на  , тогда
, тогда 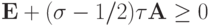 — условие устойчивости схемы с весами.
— условие устойчивости схемы с весами.
Следствие. Неявная схема  безусловно устойчива в норме ||.|| = (., .)1/2 (аналог нормы L2 ).
безусловно устойчива в норме ||.|| = (., .)1/2 (аналог нормы L2 ).
Докажем теперь, что из равномерной устойчивости однородной разностной схемы следует устойчивость по правой части.
Рассмотрим уравнение
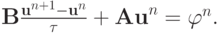
Умножив это равенство скалярно на  получим
получим
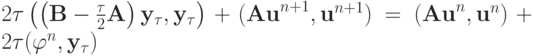
(это — энергетическое множество для неоднородного уравнения). Кроме того,
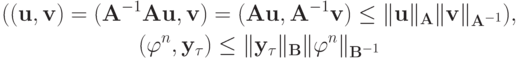
(аналог неравенства Коши - Буняковского).
Теперь используем  - неравенство
- неравенство
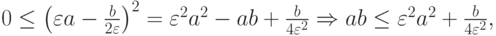
тогда получаем
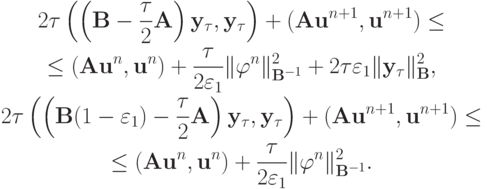
Выбираем 
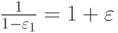
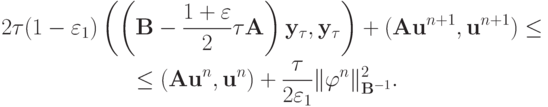
Пусть

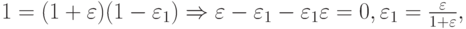
получаем
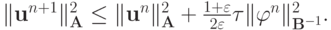
Откуда сразу следует
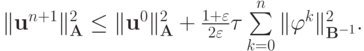 |
( 1.9) |
Таким образом, для неоднородной разностной схемы доказана следующая теорема.
Теорема. Для разностной схемы вида
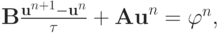
где  — постоянный (т.е. не зависящий явно от n ) положительно определенный самосопряженный оператор, а
— постоянный (т.е. не зависящий явно от n ) положительно определенный самосопряженный оператор, а 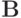 удовлетворяет условию
удовлетворяет условию
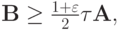
где 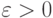 не зависит от сеточных параметров , выполнена априорная оценка (1.9).
не зависит от сеточных параметров , выполнена априорная оценка (1.9).
Вообще, в силу того, что разностная схема устойчива по начальным данным при  , из равномерной устойчивости по начальным данным следует устойчивость по правой части.
, из равномерной устойчивости по начальным данным следует устойчивость по правой части.
Так как  , то
, то  , тогда
, тогда
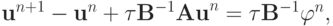
или
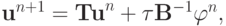
где  — оператор послойного перехода.
— оператор послойного перехода.
Равномерная устойчивость по начальным данным означает, что 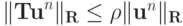 . Тогда из предыдущего равенства с использованием неравенства треугольника получим
. Тогда из предыдущего равенства с использованием неравенства треугольника получим
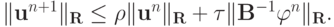
Применяя оценку n раз , получим априорную оценку для устойчивости по правой части с использованием энергетической нормы, порождаемой оператором 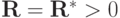 :
:

Теперь попробуем обобщить полученные результаты на случай операторов , зависящих от времени.
Для начала рассмотрим аппроксимацию типа Кранка - Николсона
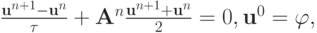
при этом 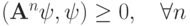 . Самый простой способ рассмотрения этого уравнения — разрешить его (в
операторном виде) относительно
. Самый простой способ рассмотрения этого уравнения — разрешить его (в
операторном виде) относительно 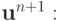

Оценим 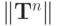 . Воспользуемся тем, что
. Воспользуемся тем, что
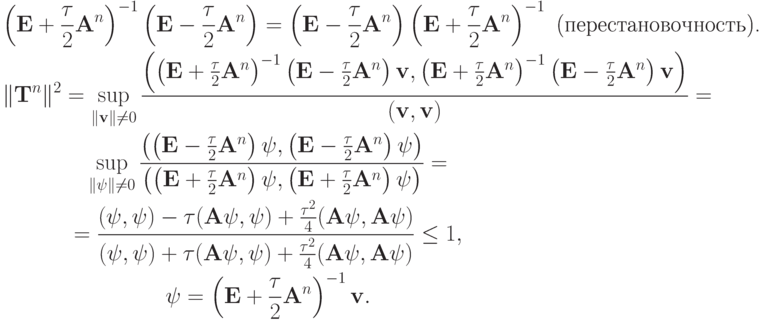
Факт, что  , носит название леммы Келлога.
, носит название леммы Келлога.
Для сеточной функции используем норму  . Подобный результат уже был получен при постоянном (не зависящем от времени)
. Подобный результат уже был получен при постоянном (не зависящем от времени)  .
.
Везде в доказательствах существенную роль играет то, что 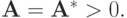 Может получиться так, что
Может получиться так, что 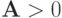 , но
, но  :
:
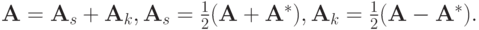
В этом случае многие свойства разностных схем аналогичны доказанным выше.
Может быть так, что 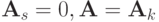 . Тогда
. Тогда

в силу кососимметричности оператора  . Например:
. Например: