НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

1.4. Задачи

Построить разностную схему, аппроксимирующую задачу Коши для уравнения переноса
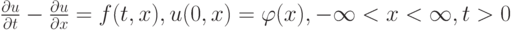
$\frac{{\partial}u}{{\partial}t} - \frac{\partial u}{{\partial}x} = f(t , x), u(0, x) = {\varphi}(x), - \infty < x < \infty , t > 0$

с помощью аппроксимации первых производных со вторым порядком точности.

Решение. Аппроксимация уравнения переноса со вторым порядком точности по схеме с центральными разностями

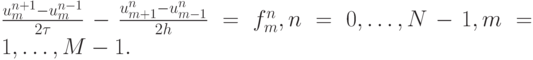
$\frac{{u_m^{n + 1} - u_m^{n - 1}}}{{2{\tau}}} - \frac{{u_{m + 1}^{n} - u_{m - 1}^{n}}}{{2h}} = f_m^{n}, n = 0, \ldots , N - 1 , m = 1 , \ldots , M - 1.$

Для аппроксимации начальных условий необходимо задать не только $u_m^0 = {\varphi}_m$ , но и значение 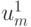, которое можно вычислить с помощью, например, формулы Тейлора:

$u_m^1 = u_m^0 +{\tau}\left({\frac{{\partial}u}{{\partial}{t}}}\right)_m^0 + O({\tau}^2 ) \approx u_m^0 + {\tau}\left({\frac{{\partial}u}{{\partial}t}}\right)_m^0.$

Поскольку
$$ \frac{{\partial}u}{{\partial}t} - \frac{{\partial}u}{{\partial}x} = f(t , x)$
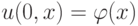и $u(0, x) = \varphi (x) $$ , то

$\left({\frac{{\partial}u}{{\partial}t}}\right)_m^0 = \left({\frac{{\partial}u}{{\partial}x}}\right)_m^0 + f(0, x) = \left[{\varphi^{\prime}_x (x)}\right]_m^0 + f_m^0.$

В таком случае аппроксимация задачи будет

$\begin{gather*} \frac{{u_m^{n + 1} -u_m^{n - 1}}}{{2{\tau}}} - \frac{{u_{m + 1}^{n} - u_{m - 1}^{n}}}{{2h}} = f_m^{n}, n = 0, \ldots , N - 1 , m = 1 , \ldots , M - 1. \\ u_m^0 = \varphi_m , m = 0, \ldots , M , \\ u_m^1 = \varphi_m +{\tau}\left[{\left({\varphi^{\prime}_x }\right)_m^0 + f_m^0 }\right] \end{gather*}$

В этом примере пришлось конструировать дополнительное второе начальное условие, поскольку исходное дифференциальное уравнение имеет первый порядок, а разностное — второй.
Исследовать устойчивость разностной схемы
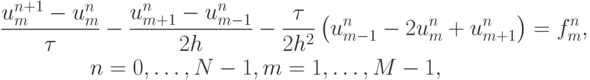
$\begin{gather*} \frac{u_m^{n + 1} - u_m^n}{\tau} - \frac{u_{m + 1}^n - u_{m - 1}^n}{2h} - \frac{\tau}{2h^2} \left({u_{m - 1}^n - 2u_m^n + u_{m + 1}^n}\right) = f_m^n, \\ n = 0, \ldots , N - 1 , m = 1 , \ldots , M - 1 , \end{gather*}$

аппроксимирующей задачу Коши для уравнения переноса.

Решение. Воспользуемся спектральным признаком. Подставляем в разностную схему решение в виде: 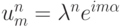$u_m^n = {\lambda}^{n} e^{im{\alpha}}$ и рассматриваем однородное уравнение.

Получим

$\frac{{\lambda}- 1}{\tau} - \frac{e^{im{\alpha}} - e^{- im{\alpha}}}{2h} - \frac{\tau}{2h^2} \left({e^{- im {\alpha}} - 2 + e^{im {\alpha}}}\right) = 0,$

откуда

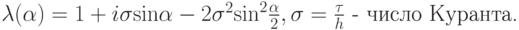
${\lambda}({\alpha}) = 1 + i{\sigma}{\sin}{\alpha}- 2{\sigma}^2 {\sin}^2 \frac{\alpha}{2}, {\sigma} = \frac{\tau}{h} \mbox{ - число Куранта.}$

Вычислим границы спектра. Для этого вычислим

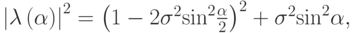
$\left| {{\lambda}\left({\alpha}\right)}\right|^2 = \left({1 - 2 {\sigma}^2{\sin}^2 \frac{{\alpha}}{2}}\right)^2 + {\sigma}^2{\sin}^2{\alpha},$

а затем расстояние 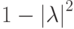$1 - \left| {\lambda}\right|^2$ . Проведем необходимые вычисления:

$\begin{gather*} \left({1 - 2 {\sigma}^2 {\sin}^2 \frac{{\alpha}}{2}}\right)^2 + {\sigma}^2 {\sin}^2 {\alpha} = 1 - 4 {\sigma}^2 {\sin}^2 \frac{{\alpha}}{2} + 4 {\sigma}^2 {\sin}^2 {\alpha} = \\ = 1 + 4 {\sigma}^4 {\sin}^4 \frac{{\alpha}}{2} + \left({- 4 {\sigma}^4 {\sin}^4 \frac{{\alpha}}{2} + {\sigma}^2 {\sin}^2 {\alpha}}\right) = \\ = 1 + 4 {\sigma}^4 {\sin}^2 \frac{{\alpha}}{2} + \left({- 4 {\sigma}^2 {\sin}^2 \frac{{\alpha}}{2} + {\sigma}^2 4 {\sin}^2 \frac{{\alpha}}{2} \cos ^2 \frac{{\alpha}}{2}}\right) = \\ = 1 + 4 {\sigma}^4 {\sin}^2 \frac{{\alpha}}{2} + \left[{- 4 {\sigma}^2 {\sin}^2 \frac{{\alpha}}{2} + {\sigma}^2 4 {\sin}^2 \frac{{\alpha}}{2} \left({1 - {\sin}^2 \frac{{\alpha}}{2}}\right)}\right] = \\ = 1 + 4 {\sigma}^4 {\sin}^2 \frac{{\alpha}}{2} - 4 {\sigma}^2 {\sin}^2 \frac{\alpha}{2}. \end{gather*}$

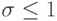Условие устойчивости выполнено, если правая часть неотрицательна, что достигается при ${\sigma}\le 1$ .
Исследовать устойчивость явной разностной схемы
$\begin{gather*} \frac{{u_{ml}^{n + 1} - u_{ml}^{n}}}{\tau} - \frac{{u_{m - 1 , l}^{n} - 2u_{ml}^{n} + u_{m + 1 , l}^{n}}}{{h^2}} - \frac{{u_{m , l - 1}^{n} - 2u_{{m , l}}^{n} + u_{{m , l} + 1}^{n}}}{{h^2}} = 0, \\ n = 0, \ldots , N - 1 , m = 1 , \ldots , M - 1 , l = 1 , \ldots , L - 1 , \end{gather*}$

аппроксимирующую задачу Коши для уравнения в частных производных

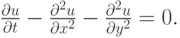
$\frac{{\partial}u}{{\partial}t} - \frac{{{\partial}^2 u}}{{{\partial}x^2}} - \frac{{{\partial}^2 u}}{{{\partial}y^2}} = 0.$

Решение. Воспользуемся спектральным признаком устойчивости фон Неймана, представив разностное решение в виде

$u_{ml}^n = {\lambda}^{n} e^{i{\alpha}m + i{\beta}n}.$
После подстановки в разностное уравнение, получим

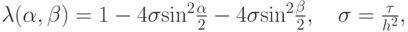
${\lambda}({\alpha}, \beta ) = 1 - 4 {\sigma}{\sin}^2 \frac{{\alpha}}{2} - 4 {\sigma}{\sin}^2 \frac{\beta }{2}, \quad {\sigma} = \frac{\tau}{{h^2}},$

откуда следует 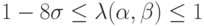$1 - 8 {\sigma} \le {\lambda}({\alpha}, \beta ) \le 1$ . Окончательно условие устойчивости разностной схемы будет ${\sigma}\le 1/4$ .
Исследовать на устойчивость разностную схему
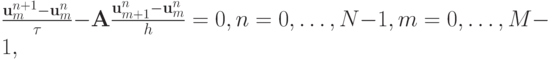
$\frac{{\mathbf{u}_m^{n + 1} - \mathbf{u}_m^{n}}}{\tau} - {\mathbf{A}} \frac{{\mathbf{u}_{m + 1}^{n} - \mathbf{u}_m^{n}}}{h} = 0, n = 0, \ldots , N - 1 , m = 0, \ldots , M - 1 ,$

(где 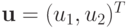$\mathbf{u} = (u_1 , u_2)^{T}$ , — вектор, 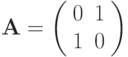$\mathbf{A} = \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array} \right)$ , — матрица 2 x 2 ), аппроксимирующую систему уравнений в частных производных

$\frac{{\partial}u_1}{{\partial}t} - \frac{\partial u_2}{{\partial}x} = 0, \frac{{\partial}u_2}{{\partial}t} - \frac{{\partial}u_1}{{\partial}x} = 0; \frac{{{\partial}\mathbf{u}}}{{\partial}t} - \mathbf{A} \frac{{{\partial}\mathbf{u}}}{{\partial}x} = 0, t > 0, - \infty < x < \infty .$

Решение. Подставим в разностную схему решение в виде

${\mathbf{u}}_m^{n} = {\lambda}^{n}\left( \begin{array}{cc} {u_1^0 } \\ {u_2^0 } \\ \end{array} \right)e^{i {\alpha}m} = {\lambda}^{n}\mathbf{u}^0 e^{i {\alpha}m}.$
После подстановки в разностное уравнение, получим

$({\lambda}- 1){\mathbf{u}}^0 - {\sigma}(e^{i {\alpha}} - 1){\mathbf{Au}}^0 = 0, {\sigma} ={\tau}/h \mbox{ - число Куранта.}$
Это уравнение можно рассматривать как векторную запись СЛАУ относительно $\mathbf{u}^0$

$\left( \begin{array}{cc} {{\lambda}- 1} & {- {\sigma}(e^{i {\alpha}} - 1)} \\ {- {\sigma}(e^{i {\alpha}} - 1)} & {{\lambda}- 1} \\ \end{array} \right) \left( \begin{array}{l} {u_1^0 } \\ {u_2^0 } \\ \end{array} \right) = 0.$
Система имеет нетривиальное решение только тогда, когда определитель матрицы обращается в нуль, т.е.

$({\lambda}- 1)^2 = {\sigma}^2 (e^{i {\alpha}} - 1)^2,$
откуда

$\lambda_1 = 1 - {\sigma}+ {\sigma}e^{i \alpha}, \quad \lambda_2 = 1 + {\sigma}- {\sigma}e^{i {\alpha}}.$
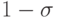Эти два корня пробегают окружности радиуса $\sigma$ с центрами в точках $1 - \sigma$ и $1 + \sigma$ . Условие устойчивости не выполнено ни при каком значении числа Куранта.