Общие динамические системы
Мы ввели фиктивный класс  смысл, которого только в том, чтобы
быть родителем для классов
смысл, которого только в том, чтобы
быть родителем для классов  и
и  - соответственно для
непрерывной и дискретной динамических систем. Мы также сразу
создали два наследника класса
- соответственно для
непрерывной и дискретной динамических систем. Мы также сразу
создали два наследника класса  для различного типа
динамических систем.
для различного типа
динамических систем.
В качестве первого примера динамической системы мы рассмотрим
отображение Хенона. Фазовым множеством здесь является множество  , время дискретное, а отображение задается формулой
, время дискретное, а отображение задается формулой

 определено по формуле
определено по формуле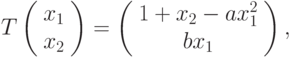
 ,
,  . В этой динамической системе возникает, так
называемый, странный аттрактор. Движение этой динамической системы
носит хаотичный характер. Реализуем и посмотрим на численные
результаты.
. В этой динамической системе возникает, так
называемый, странный аттрактор. Движение этой динамической системы
носит хаотичный характер. Реализуем и посмотрим на численные
результаты.![\begin{verbatim}
class THenon : TNDS
{
double a, b;
public THenon(double a, double b)
: base(new double[2])
{
this.a = a;
this.b = b;
}
public void Set_x1(double x1)
{
((double[])A)[0] = x1;
}
\end{verbatim}](/sites/default/files/tex_cache/56b4caa27ad9c1614becc6581895b29c.png)
![\begin{verbatim}
public void Set_x2(double x2)
{
((double[])A)[1] = x2;
}
public double Get_x1()
{
return ((double[])A)[0];
}
public double Get_x2()
{
return ((double[])A)[1];
}
public override void Next()
{
double x1, x2;
x1 = 1.0 + Get_x2() - a * Get_x1() * Get_x1();
x2 = b * Get_x1();
Set_x1(x1);
Set_x2(x2);
Inc();
}
}
\end{verbatim}](/sites/default/files/tex_cache/ee581e3731218ef5be3f9ca3fd2fb8a2.png)
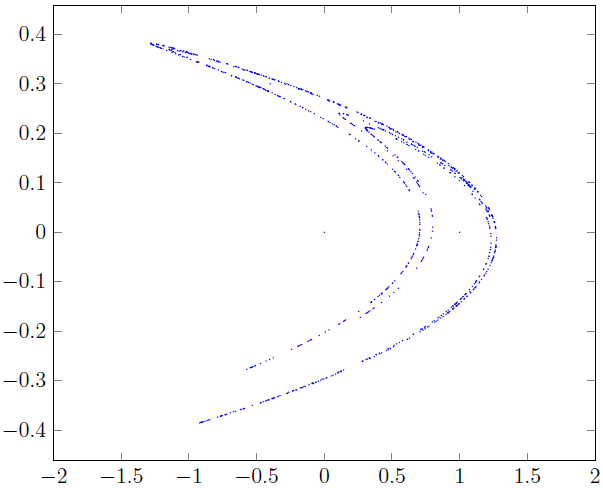
Запустим наш класс для расчета первых  точек, и на рисунке
19.1 приведем фазовый портрет.
точек, и на рисунке
19.1 приведем фазовый портрет.

В качестве примера непрерывной динамической системы мы рассмотрим
нелинейный осциллятор Ван-дер-Поля. Фазовое пространство этой
динамической системы также двумерная плоскость: 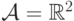 , время
непрерывное, а полугруппа преобразования задается решением задачи
Коши для следующего нелинейного дифференциального уравнения
второго порядка.
, время
непрерывное, а полугруппа преобразования задается решением задачи
Коши для следующего нелинейного дифференциального уравнения
второго порядка.

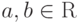 --- параметры системы. Параметр
--- параметры системы. Параметр 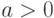 называется
параметром возбуждения.
называется
параметром возбуждения.Реализуем соответствующий класс на C#.
![\begin{verbatim}
class TPole : TRDS
{
TPoleRK RK;
double h;
public TPole(double a, double b, double h)
: base(new double[2])
{
this.h = h;
RK = new TPoleRK(a, b);
Set_x1(10.0);
Set_x2(10.0);
RK.SetInit(0, new double[] { Get_x1(), Get_x2() });
}
\end{verbatim}](/sites/default/files/tex_cache/b0076cbb654269dd2a19afeec4ee3c52.png)
![\begin{verbatim}
public void Set_x1(double x1)
{
((double[])A)[0] = x1;
}
public void Set_x2(double x2)
{
((double[])A)[1] = x2;
}
public double Get_x1()
{
return ((double[])A)[0];
}
public double Get_x2()
{
return ((double[])A)[1];
}
public override void Next()
{
RK.NextStep(h);
Inc(h);
Set_x1(RK.Y[0]);
Set_x2(RK.Y[1]);
}
}
\end{verbatim}](/sites/default/files/tex_cache/ba4de9751cecc5d1a7780a47db24bd3c.png)
![\begin{verbatim}
class TPoleRK : TRungeKutta
{
double a, b;
public TPoleRK(double a, double b) : base(2)
{
this.a = a;
this.b = b;
}
public override void F(double t, double[] Y,
ref double[] FY)
{
FY[0] = Y[1];
FY[1] = a * (1 - b * Y[0] * Y[0]) * Y[1] - Y[0];
}
}
\end{verbatim}](/sites/default/files/tex_cache/4fe82733497b82610b85b684f896f5db.png)
Теперь проведем вычислительный эксперимент.

В результате мы получим фазовый портрет, который представлен на рисунке 19.2. Мы видим, что наша динамическая система имеет так называемый предельный цикл.
Ключевые термины
Абстрактно заданная динамическая система - динамическая система на множестве, заданная с помощью полугруппы преобразований этого множества.
Конечный автомат - абстрактный автомат, моделирующий конечную динамическую систему.
Динамическая система - математическая модель системы, процессы в которой развиваются во времени.
Фазовые координаты - элементы фазового пространства, характеризующие состояние системы.
Краткие итоги: Дано общее определение динамической системы. Реализованы классы для моделирования динамических систем и проведены вычислительные эксперименты. Промоделировано отображение Хенона и нелинейный осциллятор Ван-дер-Поля.