|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Основы вероятностно-статистических методов описания неопределенностей
2.6. Некоторые типовые задачи прикладной статистики и методы их решения
Статистические данные и прикладная статистика. Под прикладной статистикой понимают часть математической статистики, посвященную методам обработки реальных статистических данных, а также методы сбора данных, соответствующее математическое и программное обеспечение. Таким образом, чисто математические задачи не включают в прикладную статистику.
Под статистическими данными понимают числовые или нечисловые значения контролируемых параметров (признаков) исследуемых объектов, которые получены в результате наблюдений (измерений, анализов, испытаний, опытов и т.д.) определенного числа признаков, у каждой единицы, вошедшей в исследование. Способы получения статистических данных и объемы выборок устанавливают, исходя из постановок конкретной прикладной задачи на основе методов математической теории планирования эксперимента.
Результат наблюдения  исследуемого признака
исследуемого признака  (или совокупности исследуемых признаков
(или совокупности исследуемых признаков  ) у
) у  -й единицы выборки отражает количественные и/или качественные свойства обследованной единицы с номером
-й единицы выборки отражает количественные и/или качественные свойства обследованной единицы с номером  (здесь
(здесь 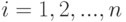 , где
, где  - объем выборки). Деление прикладной статистики на направления соответственно виду обрабатываемых результатов наблюдений (т.е. на статистику случайных величин, многомерный статистический анализ, статистику временных рядов и статистику объектов нечисловой природы) обсуждалось выше.
- объем выборки). Деление прикладной статистики на направления соответственно виду обрабатываемых результатов наблюдений (т.е. на статистику случайных величин, многомерный статистический анализ, статистику временных рядов и статистику объектов нечисловой природы) обсуждалось выше.
Результаты наблюдений 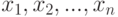 , где
, где  - результат наблюдения
- результат наблюдения  -ой единицы выборки, или результаты наблюдений для нескольких выборок, обрабатывают с помощью методов прикладной статистики, соответствующих поставленной задаче. Используют, как правило, аналитические методы, т.е. методы, основанные на численных расчетах (объекты нечисловой природы при этом описывают с помощью чисел). В отдельных случаях допустимо применение графических методов (визуального анализа).
-ой единицы выборки, или результаты наблюдений для нескольких выборок, обрабатывают с помощью методов прикладной статистики, соответствующих поставленной задаче. Используют, как правило, аналитические методы, т.е. методы, основанные на численных расчетах (объекты нечисловой природы при этом описывают с помощью чисел). В отдельных случаях допустимо применение графических методов (визуального анализа).
Количество разработанных к настоящему времени методов обработки данных весьма велико. Они описаны в сотнях тысяч книг и статей, а также в стандартах и других нормативно-технических и инструктивно-методических документах.
Многие методы прикладной статистики требуют проведения трудоемких расчетов, поэтому для их реализации необходимо использовать компьютеры. Программы расчетов на ЭВМ должны соответствовать современному научному уровню. Однако для единичных расчетов при отсутствии соответствующего программного обеспечения успешно используют микрокалькуляторы.
Задачи статистического анализа точности и стабильности технологических процессов и качества продукции. Статистические методы используют, в частности, для анализа точности и стабильности технологических процессов и качества продукции. Цель - подготовка решений, обеспечивающих эффективное функционирование технологических единиц и повышение качества и конкурентоспособности выпускаемой продукции. Статистические методы следует применять во всех случаях, когда по результатам ограниченного числа наблюдений требуется установить причины улучшения или ухудшения точности и стабильности технологического оборудования. Под точностью технологического процесса понимают свойство технологического процесса, обусловливающее близость действительных и номинальных значений параметров производимой продукции. Под стабильностью технологического процесса понимают свойство технологического процесса, обусловливающее постоянство распределений вероятностей для его параметров в течение некоторого интервала времени без вмешательства извне.
Целями применения статистических методов анализа точности и стабильности технологических процессов и качества продукции на стадиях разработки, производства и эксплуатации (потребления) продукции являются, в частности:
- определение фактических показателей точности и стабильности технологического процесса, оборудования или качества продукции;
- установление соответствия качества продукции требованиям нормативно-технической документации;
- проверка соблюдения технологической дисциплины;
- изучение случайных и систематических факторов, способных привести к появлению дефектов;
- выявление резервов производства и технологии;
- обоснование технических норм и допусков на продукцию;
- оценка результатов испытаний опытных образцов при обосновании требований к продукции и нормативов на нее;
- обоснование выбора технологического оборудования и средств измерений и испытаний;
- сравнение различных образцов продукции;
- обоснование замены сплошного контроля статистическим;
- выявление возможности внедрения статистических методов управления качеством продукции, и т.д.
Для достижения перечисленных выше целей применяют различные методы описания данных, оценивания и проверки гипотез. Приведем примеры постановок задач.
Задачи одномерной статистики (статистики случайных величин). Сравнение математических ожиданий проводят в тех случаях, когда необходимо установить соответствие показателей качества изготовленной продукции и эталонного образца. Это - задача проверки гипотезы:
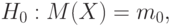
 - значение, соответствующее эталонному образцу;
- значение, соответствующее эталонному образцу;  - случайная величина, моделирующая результаты наблюдений. В зависимости от формулировки вероятностной модели ситуации и альтернативной гипотезы сравнение математических ожиданий проводят либо параметрическими, либо непараметрическими методами.
- случайная величина, моделирующая результаты наблюдений. В зависимости от формулировки вероятностной модели ситуации и альтернативной гипотезы сравнение математических ожиданий проводят либо параметрическими, либо непараметрическими методами.Сравнение дисперсий проводят тогда, когда требуется установить отличие рассеивания показателя качества от номинального. Для этого проверяют гипотезу:

Ряд иных постановок задач одномерной статистики приведен ниже. Не меньшее значение, чем задачи проверки гипотез, имеют задачи оценивания параметров. Они, как и задачи проверки гипотез, в зависимости от используемой вероятностной модели ситуации делятся на параметрические и непараметрические.
В параметрических задачах оценивания принимают вероятностную модель, согласно которой результаты наблюдений 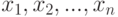 рассматривают как реализации
рассматривают как реализации  независимых случайных величин с функцией распределения
независимых случайных величин с функцией распределения 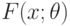 . Здесь
. Здесь  - неизвестный параметр, лежащий в пространстве параметров
- неизвестный параметр, лежащий в пространстве параметров  , заданном используемой вероятностной моделью. Задача оценивания состоит в определении точечных оценок и доверительных границ (либо доверительной области) для параметра
, заданном используемой вероятностной моделью. Задача оценивания состоит в определении точечных оценок и доверительных границ (либо доверительной области) для параметра  .
.
Параметр  - либо число, либо вектор фиксированной конечной размерности. Так, для нормального распределения
- либо число, либо вектор фиксированной конечной размерности. Так, для нормального распределения 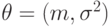 - двумерный вектор, для биномиального
- двумерный вектор, для биномиального  - число, для гамма-распределения
- число, для гамма-распределения 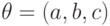 - трехмерный вектор и т.д.
- трехмерный вектор и т.д.
В современной математической статистике разработан ряд общих методов определения оценок и доверительных границ - метод моментов, метод максимального правдоподобия, метод одношаговых оценок, метод устойчивых (робастных) оценок, метод несмещенных оценок и др. Кратко рассмотрим первые три из них. Теоретические основы различных методов оценивания и полученные с их помощью конкретные правила определения оценок и доверительных границ для тех или иных параметрических семейств распределений рассмотрены в специальной литературе, включены в нормативно-техническую и инструктивно-методическую документацию.
Метод моментов основан на использовании выражений для моментов рассматриваемых случайных величин через параметры их функций распределения. Оценки метода моментов получают, подставляя выборочные моменты вместо теоретических в функции, выражающие параметры через моменты.
В методе максимального правдоподобия, разработанном в основном Р.А.Фишером, в качестве оценки параметра  берут значение
берут значение  , для которого максимальна так называемая функция правдоподобия
, для которого максимальна так называемая функция правдоподобия
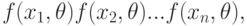
где 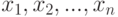 - результаты наблюдений;
- результаты наблюдений; 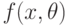 - их плотность распределения, зависящая от параметра
- их плотность распределения, зависящая от параметра  , который необходимо оценить.
, который необходимо оценить.
Оценки максимального правдоподобия, как правило, эффективны (или асимптотически эффективны) и имеют меньшую дисперсию, чем оценки метода моментов. В отдельных случаях формулы для них выписываются явно (нормальное распределение, экспоненциальное распределение без сдвига). Однако чаще для их нахождения необходимо численно решать систему трансцендентных уравнений (распределения Вейбулла-Гнеденко, гамма). В подобных случаях целесообразно использовать не оценки максимального правдоподобия, а другие виды оценок, прежде всего одношаговые оценки. В литературе их иногда не вполне точно называют "приближенные оценки максимального правдоподобия". При достаточно больших объемах выборок они имеют столь же хорошие свойства, как и оценки максимального правдоподобия. Поэтому их следует рассматривать не как "приближенные", а как оценки, полученные по другому методу, не менее обоснованному и эффективному, чем метод максимального правдоподобия. Одношаговые оценки вычисляют по явным формулам (см. "Оценивание" , а также [ [ 2.14 ] ]).
В непараметрических задачах оценивания принимают вероятностную модель, в которой результаты наблюдений 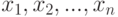 рассматривают как реализации
рассматривают как реализации  независимых случайных величин с функцией распределения
независимых случайных величин с функцией распределения  общего вида. От
общего вида. От  требуют лишь выполнения некоторых условий типа непрерывности, существования математического ожидания и дисперсии и т.п. Подобные условия не являются столь жесткими, как условие принадлежности к определенному параметрическому семейству.
требуют лишь выполнения некоторых условий типа непрерывности, существования математического ожидания и дисперсии и т.п. Подобные условия не являются столь жесткими, как условие принадлежности к определенному параметрическому семейству.
В непараметрической постановке оценивают либо характеристики случайной величины (математическое ожидание, дисперсию, коэффициент вариации), либо ее функцию распределения, плотность и т.п. Так, в силу закона больших чисел выборочное среднее арифметическое \overline{x} является состоятельной оценкой математического ожидания 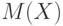 (при любой функции распределения
(при любой функции распределения  результатов наблюдений, для которой математическое ожидание существует). С помощью центральной предельной теоремы определяют асимптотические доверительные границы
результатов наблюдений, для которой математическое ожидание существует). С помощью центральной предельной теоремы определяют асимптотические доверительные границы

где  - доверительная вероятность,
- доверительная вероятность, 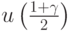 - квантиль порядка
- квантиль порядка 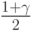 стандартного нормального распределения
стандартного нормального распределения  с нулевым математическим ожиданием и единичной дисперсией,
с нулевым математическим ожиданием и единичной дисперсией,  - выборочное среднее арифметическое,
- выборочное среднее арифметическое,  - выборочное среднее квадратическое отклонение. Термин "асимптотические доверительные границы" означает, что вероятности
- выборочное среднее квадратическое отклонение. Термин "асимптотические доверительные границы" означает, что вероятности

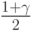 ,
, 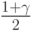 и
и  соответственно при
соответственно при  , но, вообще говоря, не равны этим значениям при конечных
, но, вообще говоря, не равны этим значениям при конечных  . Практически асимптотические доверительные границы дают достаточную точность при
. Практически асимптотические доверительные границы дают достаточную точность при  порядка 10.
порядка 10.Второй пример непараметрического оценивания - оценивание функции распределения. По теореме Гливенко эмпирическая функция распределения 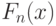 является состоятельной оценкой функции распределения
является состоятельной оценкой функции распределения  . Если
. Если  - непрерывная функция, то на основе теоремы Колмогорова доверительные границы для функции распределения
- непрерывная функция, то на основе теоремы Колмогорова доверительные границы для функции распределения  задают в виде
задают в виде
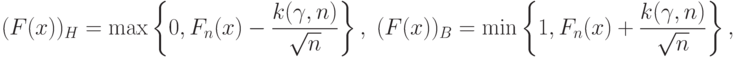
где  - квантиль порядка
- квантиль порядка  распределения статистики Колмогорова при объеме выборки
распределения статистики Колмогорова при объеме выборки  (напомним, что распределение этой статистики не зависит от
(напомним, что распределение этой статистики не зависит от  ).
).
Правила определения оценок и доверительных границ в параметрическом случае строятся на основе параметрического семейства распределений 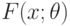 . При обработке реальных данных возникает вопрос - соответствуют ли эти данные принятой вероятностной модели, т.е. статистической гипотезе о том, что результаты наблюдений имеют функцию распределения из семейства
. При обработке реальных данных возникает вопрос - соответствуют ли эти данные принятой вероятностной модели, т.е. статистической гипотезе о том, что результаты наблюдений имеют функцию распределения из семейства 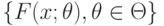 при некотором
при некотором  ? Такие гипотезы называют гипотезами согласия, а критерии их проверки - критериями согласия.
? Такие гипотезы называют гипотезами согласия, а критерии их проверки - критериями согласия.
Если истинное значение параметра  известно, функция распределения
известно, функция распределения 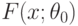 непрерывна, то для проверки гипотезы согласия часто применяют критерий Колмогорова, основанный на статистике
непрерывна, то для проверки гипотезы согласия часто применяют критерий Колмогорова, основанный на статистике
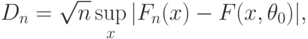
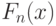 - эмпирическая функция распределения.
- эмпирическая функция распределения.Если истинное значение параметра 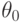 неизвестно, например, при проверке гипотезы о нормальности распределения результатов наблюдения (т.е. при проверке принадлежности этого распределения к семейству нормальных распределений), то иногда используют статистику
неизвестно, например, при проверке гипотезы о нормальности распределения результатов наблюдения (т.е. при проверке принадлежности этого распределения к семейству нормальных распределений), то иногда используют статистику
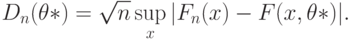
Она отличается от статистики Колмогорова 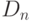 тем, что вместо истинного значения параметра
тем, что вместо истинного значения параметра 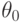 подставлена его оценка
подставлена его оценка 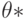 .
.
Распределение статистики  сильно отличается от распределения статистики
сильно отличается от распределения статистики 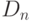 . В качестве примера рассмотрим проверку нормальности, когда
. В качестве примера рассмотрим проверку нормальности, когда 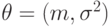 , а
, а  . Для этого случая квантили распределений статистик
. Для этого случая квантили распределений статистик 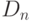 и
и  приведены в табл.2.5 (см., например, [
[
2.13
]
]). Таким образом, квантили отличаются примерно в 1,5 раза.
приведены в табл.2.5 (см., например, [
[
2.13
]
]). Таким образом, квантили отличаются примерно в 1,5 раза.
 |
0,85 | 0,90 | 0,95 | 0,975 | 0,99 |
|---|---|---|---|---|---|
Квантили порядка  для для 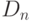
|
1,138 | 1,224 | 1,358 | 1,480 | 1,626 |
Квантили порядка  для для 
|
0,775 | 0,819 | 0,895 | 0,955 | 1,035 |
При первичной обработке статистических данных важной задачей является исключение результатов наблюдений, полученных в резульытате грубых погрешностей и промахов. Например, при просмотре данных о весе (в килограммах) новорожденных детей наряду с числами 3,500, 2,750, 4,200 может встретиться число 35,00. Ясно, что это промах, и получено ошибочное число при ошибочной записи - запятая сдвинута на один знак, в результате результат наблюдения ошибочно увеличен в 10 раз.
Статистические методы исключения резко выделяющихся результатов наблюдений основаны на предположении, что подобные результаты наблюдений имеют распределения, резко отличающиеся от изучаемых, а потому их следует исключить из выборки.
Простейшая вероятностная модель такова. При нулевой гипотезе результаты наблюдений рассматриваются как реализации независимых одинаково распределенных случайных величин 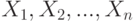 с функцией распределения
с функцией распределения  . При альтернативной гипотезе
. При альтернативной гипотезе 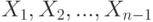 - такие же, как и при нулевой гипотезе, а
- такие же, как и при нулевой гипотезе, а 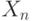 соответствует грубой погрешности и имеет функцию распределения
соответствует грубой погрешности и имеет функцию распределения 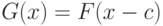 , где с велико. Тогда с вероятностью, близкой к 1 (точнее, стремящейся к 1 при росте объема выборки),
, где с велико. Тогда с вероятностью, близкой к 1 (точнее, стремящейся к 1 при росте объема выборки),
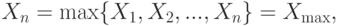
 . Критическая область имеет вид
. Критическая область имеет вид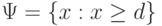
Критическое значение 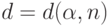 выбирают в зависимости от уровня значимости
выбирают в зависимости от уровня значимости  и объема выборки
и объема выборки  из условия
из условия
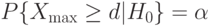 |
( 1) |
Условие (1) эквивалентно при больших  и малых
и малых  следующему:
следующему:
![F(d)=\sqrt[n]{1-\alpha}\approx1-\frac{\alpha}{n}](/sites/default/files/tex_cache/0ff2d8d73ecfb4ea719fb804e9a95cef.png) |
( 2) |
Если функция распределения результатов наблюдений  известна, то критическое значение
известна, то критическое значение  находят из соотношения (2). Если
находят из соотношения (2). Если  известна с точностью до параметров, например, известно, что
известна с точностью до параметров, например, известно, что  - нормальная функция распределения, то также разработаны правила проверки рассматриваемой гипотезы [
[
2.1
]
].
- нормальная функция распределения, то также разработаны правила проверки рассматриваемой гипотезы [
[
2.1
]
].
Однако часто вид функции распределения результатов наблюдений известен не абсолютно точно и не с точностью до параметров, а лишь с некоторой погрешностью. Тогда соотношение (2) становится практически бесполезным, поскольку малая погрешность в определении  , как можно показать, приводит к большой погрешности при определении критического значения
, как можно показать, приводит к большой погрешности при определении критического значения  из условия (2), а при фиксированном
из условия (2), а при фиксированном  уровень значимости критерия может существенно отличаться от номинального [
[
2.16
]
].
уровень значимости критерия может существенно отличаться от номинального [
[
2.16
]
].
Поэтому в ситуации, когда о  нет полной информации, однако известны математическое ожидание
нет полной информации, однако известны математическое ожидание 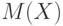 и дисперсия
и дисперсия  результатов наблюдений
результатов наблюдений 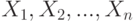 , можно использовать непараметрические правила отбраковки, основанные на неравенстве Чебышева. С помощью этого неравенства найдем критическое значение
, можно использовать непараметрические правила отбраковки, основанные на неравенстве Чебышева. С помощью этого неравенства найдем критическое значение 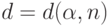 такое, что
такое, что
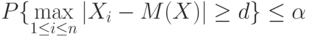 |
( 3) |
Так как
![P\{\max_{1\le i\le n}|X_i-M(X)|<d\}=[P\{|X-M(X)|<d\}]^n,](/sites/default/files/tex_cache/b951d73f3dda4fba5559e4c081e8ef39.png)
![P\{|X-M(X)|\ge d\}\le 1-\sqrt[n]{1-\alpha}\approx\frac{\alpha}{n}.](/sites/default/files/tex_cache/bb7c5667dc42fa78707e7ff6de3a7134.png) |
( 4) |
 |
( 5) |
 из условия
из условия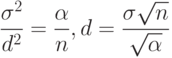 |
( 6) |
Правило отбраковки, основанное на критическом значении  , вычисленном по формуле (6), использует минимальную информацию о функции распределения
, вычисленном по формуле (6), использует минимальную информацию о функции распределения  и поэтому исключает лишь результаты наблюдений, весьма далеко отстоящие от основной массы. Другими словами, значение
и поэтому исключает лишь результаты наблюдений, весьма далеко отстоящие от основной массы. Другими словами, значение  , заданное соотношением (1), обычно много меньше, чем значение
, заданное соотношением (1), обычно много меньше, чем значение 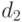 , заданное соотношением (6).
, заданное соотношением (6).
Многомерный статистический анализ. Перейдем к многомерному статистическому анализу. Его применяют при решении следующих задач:
- исследование зависимости между признаками;
- классификация объектов или признаков, заданных векторами;
- снижение размерности пространства признаков.
При этом результат наблюдений - вектор значений фиксированного числа количественных и иногда качественных признаков, измеренных у объекта. Напомним, что количественный признак - признак наблюдаемой единицы, который можно непосредственно выразить числом и единицей измерения. Количественный признак противопоставляется качественному - признаку наблюдаемой единицы, определяемому отнесением к одной из двух или более условных категорий (если имеется ровно две категории, то признак называется альтернативным). Статистический анализ качественных признаков - часть статистики объектов нечисловой природы. Количественные признаки делятся на признаки, измеренные в шкалах интервалов, отношений, разностей, абсолютной.
А качественные - на признаки, измеренные в шкале наименований и порядковой шкале. Методы обработки данных должны быть согласованы со шкалами, в которых измерены рассматриваемые признаки (см. "Описание данных" о теории измерений).
Целями исследования зависимости между признаками являются доказательство наличия связи между признаками и изучение этой связи. Для доказательства наличия связи между двумя случайными величинами  и
и  применяют корреляционный анализ. Если совместное распределение
применяют корреляционный анализ. Если совместное распределение  и
и  является нормальным, то статистические выводы основывают на выборочном коэффициенте линейной корреляции, в остальных случаях используют коэффициенты ранговой корреляции Кендалла и Спирмена, а для качественных признаков - критерий хи-квадрат.
является нормальным, то статистические выводы основывают на выборочном коэффициенте линейной корреляции, в остальных случаях используют коэффициенты ранговой корреляции Кендалла и Спирмена, а для качественных признаков - критерий хи-квадрат.
Регрессионный анализ применяют для изучения функциональной зависимости количественного признака  от количественных признаков
от количественных признаков  . Эту зависимость называют регрессионной или, кратко, регрессией. Простейшая вероятностная модель регрессионного анализа (в случае
. Эту зависимость называют регрессионной или, кратко, регрессией. Простейшая вероятностная модель регрессионного анализа (в случае 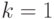 ) использует в качестве исходной информации набор пар результатов наблюдений
) использует в качестве исходной информации набор пар результатов наблюдений  , и имеет вид
, и имеет вид

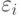 - ошибки наблюдений. Иногда предполагают, что
- ошибки наблюдений. Иногда предполагают, что 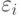 - независимые случайные величины с одним и тем же нормальным распределением
- независимые случайные величины с одним и тем же нормальным распределением  . Поскольку распределение ошибок наблюдения обычно отлично от нормального, то целесообразно рассматривать регрессионную модель в непараметрической постановке [
[
2.16
]
], т.е. при произвольном распределении
. Поскольку распределение ошибок наблюдения обычно отлично от нормального, то целесообразно рассматривать регрессионную модель в непараметрической постановке [
[
2.16
]
], т.е. при произвольном распределении 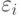 .
.Основная задача регрессионного анализа состоит в оценке неизвестных параметров  и
и  , задающих линейную зависимость
, задающих линейную зависимость  от
от  . Для решения этой задачи применяют разработанный еще в 1794 г. К.Гауссом метод наименьших квадратов, т.е. находят оценки неизвестных параметров модели
. Для решения этой задачи применяют разработанный еще в 1794 г. К.Гауссом метод наименьших квадратов, т.е. находят оценки неизвестных параметров модели  и
и  из условия минимизации суммы квадратов
из условия минимизации суммы квадратов

 и
и  .
.Описание теории регрессионного анализа и расчетные формулы приведены в специальной литературе [
[
1.7
]
,
[
2.16
]
,
[
1.22
]
]. В рамках этой теории разработаны методы точечного и интервального оценивания параметров, задающих функциональную зависимость, а также непараметрические методы оценивания этой зависимости, методы проверки различных гипотез, связанных с регрессионными зависимостями. Выбор планов эксперимента, т.е. точек  , в которых будут проводиться эксперименты по наблюдению
, в которых будут проводиться эксперименты по наблюдению  - предмет теории планирования эксперимента [
[
2.11
]
].
- предмет теории планирования эксперимента [
[
2.11
]
].
Дисперсионный анализ применяют для изучения влияния качественных признаков на количественную переменную. Например, пусть имеются  выборок результатов измерений количественного показателя качества единиц продукции, выпущенных на
выборок результатов измерений количественного показателя качества единиц продукции, выпущенных на  станках, т.е. набор чисел
станках, т.е. набор чисел 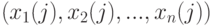 , где
, где  - номер станка,
- номер станка, 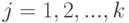 , а
, а  - объем выборки. В распространенной постановке дисперсионного анализа предполагают, что результаты измерений независимы и в каждой выборке имеют нормальное распределение
- объем выборки. В распространенной постановке дисперсионного анализа предполагают, что результаты измерений независимы и в каждой выборке имеют нормальное распределение 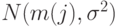 с одной и той же дисперсией. Хорошо разработаны и непараметрические постановки [
[
2.21
]
].
с одной и той же дисперсией. Хорошо разработаны и непараметрические постановки [
[
2.21
]
].
Проверка однородности качества продукции, т.е. отсутствия влияния номера станка на качество продукции, сводится к проверке гипотезы

