|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Многомерный статистический анализ
В многомерном статистическом анализе выборка состоит из элементов многомерного пространства. Отсюда и название этого раздела прикладной статистики. Из многих задач многомерного статистического анализа рассмотрим основные - корреляцию, восстановление зависимости, классификацию, уменьшение размерности, индексы.
9.1. Коэффициенты корреляции
Термин "корреляция" означает "связь". В прикладной статистике этот термин обычно используется в сочетании "коэффициенты корреляции". Рассмотрим линейный и непараметрические парные коэффициенты корреляции.
Обсудим способы измерения связи между двумя случайными переменными. Пусть исходными данными является набор случайных векторов  . Выборочным коэффициентом корреляции, более подробно, выборочным линейным парным коэффициентом корреляции К. Пирсона, как известно, называется число
. Выборочным коэффициентом корреляции, более подробно, выборочным линейным парным коэффициентом корреляции К. Пирсона, как известно, называется число

Если 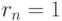 , то
, то 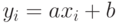 , причем
, причем  . Если же
. Если же 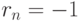 , то
, то 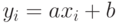 , причем
, причем 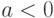 . Таким образом, близость коэффициента корреляции к 1 (по абсолютной величине) говорит о достаточно тесной линейной связи.
. Таким образом, близость коэффициента корреляции к 1 (по абсолютной величине) говорит о достаточно тесной линейной связи.
Если случайные векторы  независимы и одинаково распределены, то выборочный коэффициент корреляции сходится к теоретическому при безграничном возрастании объема выборки:
независимы и одинаково распределены, то выборочный коэффициент корреляции сходится к теоретическому при безграничном возрастании объема выборки:
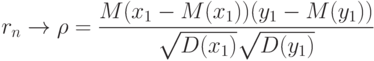
Более того, выборочный коэффициент корреляции является асимптотически нормальным. Это означает, что
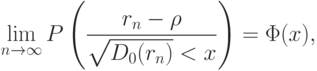
 - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1, а
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1, а  - асимптотическая дисперсия выборочного коэффициента корреляции. Она имеет довольно сложное выражение, приведенное в монографии [
[
2.10
]
, с.393]:
- асимптотическая дисперсия выборочного коэффициента корреляции. Она имеет довольно сложное выражение, приведенное в монографии [
[
2.10
]
, с.393]:
Здесь под  понимаются теоретические центральные моменты порядка
понимаются теоретические центральные моменты порядка  и
и  , а именно,
, а именно,
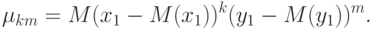
Коэффициенты корреляции типа 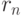 используются во многих алгоритмах многомерного статистического анализа. В теоретических рассмотрениях часто считают, что случайные векторы
используются во многих алгоритмах многомерного статистического анализа. В теоретических рассмотрениях часто считают, что случайные векторы 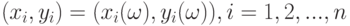 , имеют двумерное нормальное распределение. Распределения реальных данных, как правило, отличны от нормальных (см.
"Описание данных"
). Почему же распространено представление о двумерном нормальном распределении? Дело в том, что теория в этом случае более проста. В частности, равенство 0 теоретического коэффициента корреляции эквивалентно независимости случайных величин. Поэтому проверка независимости сводится к проверке статистической гипотезы о равенстве 0 теоретического коэффициента корреляции. Эта гипотеза принимается, если
, имеют двумерное нормальное распределение. Распределения реальных данных, как правило, отличны от нормальных (см.
"Описание данных"
). Почему же распространено представление о двумерном нормальном распределении? Дело в том, что теория в этом случае более проста. В частности, равенство 0 теоретического коэффициента корреляции эквивалентно независимости случайных величин. Поэтому проверка независимости сводится к проверке статистической гипотезы о равенстве 0 теоретического коэффициента корреляции. Эта гипотеза принимается, если 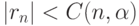 , где
, где 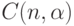 - некоторое граничное значение, зависящее от объема выборки
- некоторое граничное значение, зависящее от объема выборки  и уровня значимости
и уровня значимости  .
.
Если предположение о двумерной нормальности не выполнено, то из равенства 0 теоретического коэффициента корреляции не вытекает независимость случайных величин. Нетрудно построить пример случайного вектора, для которого коэффициент корреляции равен 0, но координаты зависимы. Кроме того, для проверки гипотез о коэффициенте корреляции нельзя пользоваться таблицами, рассчитанными в предположении нормальности. Можно построить правила принятия решений на основе асимптотической нормальности выборочного коэффициента корреляции. Но есть и другой путь - перейти к непараметрическим коэффициентам корреляции, одинаково пригодным при любом непрерывном распределении случайного вектора.
Для расчета непараметрического коэффициента ранговой корреляции Спирмена необходимо сделать следующее. Для каждого  рассчитать его ранг
рассчитать его ранг  в вариационном ряду, построенном по выборке
в вариационном ряду, построенном по выборке  . Для каждого
. Для каждого  рассчитать его ранг
рассчитать его ранг  в вариационном ряду, построенном по выборке
в вариационном ряду, построенном по выборке  . Для набора из
. Для набора из  пар
пар  вычислить линейный коэффициент корреляции. Он называется коэффициентом ранговой корреляции, поскольку определяется через ранги. В качестве примера рассмотрим данные из табл.9.1 (см. монографию [
[
9.7
]
]).
вычислить линейный коэффициент корреляции. Он называется коэффициентом ранговой корреляции, поскольку определяется через ранги. В качестве примера рассмотрим данные из табл.9.1 (см. монографию [
[
9.7
]
]).
 |
1 | 2 | 3 | 4 | 5 |
 |
5 | 10 | 15 | 20 | 25 |
 |
6 | 7 | 30 | 81 | 300 |
 |
1 | 2 | 3 | 4 | 5 |
 |
1 | 2 | 3 | 4 | 5 |
Для данных табл.9.1 коэффициент линейной корреляции равен 0,83, непосредственной линейной связи нет. А вот коэффициент ранговой корреляции равен 1, поскольку увеличение одной переменной однозначно соответствует увеличению другой переменной. Во многих экономических задачах, например, при выборе инвестиционных проектов, достаточно именно монотонной зависимости одной переменной от другой.
Поскольку суммы рангов и их квадратов нетрудно подсчитать, то коэффициент ранговой корреляции Спирмена равен
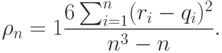
Отметим, что коэффициент ранговой корреляции Спирмена остается постоянным при любом строго возрастающем преобразовании шкалы измерения результатов наблюдений. Другими словами, он является адекватным в порядковой шкале (см. "Описание данных" ), как и другие ранговые статистики, например, статистики Вилкоксона, Смирнова, типа омега-квадрат для проверки однородности независимых выборок ( "Статистический анализ числовых величин" ).
Широко используется также коэффициент ранговой корреляции  Кендалла, коэффициент ранговой конкордации Кендалла и Б. Смита и др. Наиболее подробное обсуждение этой тематики содержится в монографии [
[
9.5
]
], необходимые для практических расчетов таблицы имеются в справочнике [
[
2.1
]
]. Дискуссия о выборе вида коэффициентов корреляции продолжается до настоящего времени [
[
9.7
]
].
Кендалла, коэффициент ранговой конкордации Кендалла и Б. Смита и др. Наиболее подробное обсуждение этой тематики содержится в монографии [
[
9.5
]
], необходимые для практических расчетов таблицы имеются в справочнике [
[
2.1
]
]. Дискуссия о выборе вида коэффициентов корреляции продолжается до настоящего времени [
[
9.7
]
].
