НОУ ИНТУИТ | Прикладная статистика. Лекция 6: Оценивание

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2009 | Доступ: свободный | Студентов: 4083 / 1035 | Оценка: 4.66 / 4.45 | Длительность: 54:13:00

Темы: Математика, Экономика

Специальности: Экономист

|

Вам нравится? Нравится 61 студенту

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В лекции рассматриваются различные методы оценивания параметров, в том числе метод моментов, максимального правдоподобия, одношаговые оценки, а также задача параметрической регрессии. Затрагиваются вопросы робастности статистических процедур.

Ключевые слова: размерность, пространство, евклидово пространство, значение, множитель, функция, ПО, статистика, выборка, доказательство, параметр, коэффициент вариации, вектор, математическим ожиданием, случайная величина, линеаризация, место, бесконечно малая величина, робастность, равенство, оценивание, выборочной средней, дисперсия, сочетания, статистическая гипотеза, доверительная вероятность, оценка максимального правдоподобия, выражение, класс, определение, биномиальное распределение, Произведение, логарифмическая функция правдоподобия, сходимость, локальный максимум, итерационный алгоритм, точность, группа, евклидово расстояние, метод Ньютона, матрица, нормальный закон, Единичная матрица, итерация, оценка векторов, эквивалентность, уравнение правдоподобия, системы нелинейных уравнений, координаты, отношение, коэффициент асимметрии, метод статистических испытаний, программное обеспечение, доказательство теорем, задачу аппроксимации, натуральное число, метода наименьших квадратов, минимум, очередь, мера, интеграл, числитель, компонент, минимизация, вычисление, предел, анализ данных, отрезок, прямой, грани, коэффициент корреляции, коэффициенты, целый, интервал, погрешность

6.1. Методы оценивания параметров

В прикладной статистике используются разнообразные параметрические модели. Термин "параметрический" означает, что вероятностно-статистическая модель полностью описывается конечномерным вектором фиксированной размерности. Причем эта размерность не зависит от объема выборки.

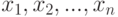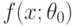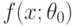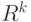Рассмотрим выборку x_1, x_2,..., x_n из распределения с плотностью $f(x;\theta_0)$ , где $f(x;\theta_0)$ - элемент параметрического семейства плотностей распределения вероятностей $\{f(x;\theta), \theta\in\Theta\}$ . Здесь $\Theta$ - заранее известное -мерное пространство параметров, являющееся подмножеством евклидова пространства R^k , а конкретное значение параметра 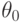$\theta_0$ статистику неизвестно. Обычно в прикладной статистике применяются параметрические семейства с k = 1,2,3 (см. "Основы вероятностно-статистических методов описания неопределенностей" ). В статистике нечисловых данных вместо плотности часто рассматриваются вероятности попадания в точки. 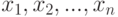Напомним, что в параметрических задачах оценивания принимают вероятностную модель, согласно которой результаты наблюдений x_1, x_2,..., x_n рассматривают как реализации n независимых случайных величин.

Задача оценивания состоит в том, чтобы оценить неизвестное статистику значение параметра 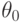$\theta_0$ наилучшим (в каком-либо смысле) образом.

Пример 1. В статистических задачах стандартизации и управления качеством используют семейство гамма-распределений. Плотность гамма-распределения имеет вид

$f(x; a,b,c)= \left\{ \begin{gathered} \frac{1}{\Gamma(a)}(x-c)^{a-1}b^{-a}\exp\left[-\frac{x-c}{b}\right],x\ge c, \\ 0,\quad x< c. \end{gathered} \right.$

( 1)

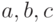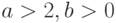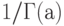Плотность вероятности в формуле (1) определяется тремя параметрами a, b, c , где a>2, b>0 . При этом является параметром формы, - параметром масштаба и - параметром сдвига. Множитель $1/\Gamma(а)$ является нормировочным, он введен, чтобы

$\int\limits_{-\infty}^{+\infty}f(x;a,b,c)dx=1.$

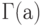Здесь $\Gamma(а)$ - одна из используемых в математике специальных функций, так называемая "гамма-функция", по которой названо и распределение, задаваемое формулой (1),

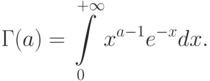
$\Gamma(a)=\int\limits_0^{+\infty}x^{a-1}e^{-x}dx.$

Подробные решения задач оценивания параметров для гамма-распределения содержатся в разработанном нами государственном стандарте ГОСТ 11.011-83 "Прикладная статистика. Правила определения оценок и доверительных границ для параметров гамма-распределения" [ [ 6.6 ] ]. В настоящее время эта публикация используется в качестве методического материала для инженерно-технических работников промышленных предприятий и прикладных научно-исследовательских институтов.

Поскольку гамма-распределение зависит от трех параметров, то имеется 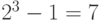2^3-1=7 вариантов постановок задач оценивания. Они описаны в табл.6.1.

Таблица 6.1. Постановки задач оценивания для параметров гамма-распределения
№ п/п	Параметр формы	Параметр масштаба	Параметр сдвига
1	Известен	Оценивается	Известен
2	Оценивается	Известен	Известен
3	Известен	Известен	Оценивается
4	Оценивается	Оценивается	Известен
5	Известен	Оценивается	Оценивается
6	Оценивается	Известен	Оценивается
7	Оценивается	Оценивается	Оценивается

В табл.6.2 приведены реальные данные о наработке резцов до предельного состояния, в часах. Упорядоченная выборка (вариационный ряд) объема n = 50 взята из государственного стандарта [ [ 6.6 ] ]. Проверка согласия данных о наработке резцов с семейством гамма-распределений проведена в "Проверка гипотез" . Именно эти данные будут служить исходным материалом для демонстрации тех или иных методов оценивания параметров.

Таблица 6.2. Наработка резцов до предельного состояния (ч)
№ п/п	Наработка	№ п/п	Наработка	№ п/п	Наработка
1	9	18	47,5	35	63
2	17,5	19	48	36	64,5
3	21	20	50	37	65
4	26,5	21	51	38	67,5
5	27,5	22	53,5	39	68,5
6	31	23	55	40	70
7	32,5	24	56	41	72,5
8	34	25	56	42	77,5
9	36	26	56,5	43	81
10	36,5	27	57,5	44	82,5
11	39	28	58	45	90
12	40	29	59	46	96
13	41	30	59	47	101,5
14	42,5	31	60	48	117,5
15	43	32	61	49	127,5
16	45	33	61,5	50	130
17	46	34	62

Выбор "наилучших" оценок в определенной параметрической модели прикладной статистики - научно-исследовательская работа, растянутая во времени. Выделим два этапа. Этап асимптотики: оценки строятся и сравниваются по их свойствам при безграничном росте объема выборки. На этом этапе рассматривают такие характеристики оценок, как состоятельность, асимптотическая эффективность и др. Этап конечных объемов выборки: оценки сравниваются, скажем, при 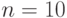n = 10 . Ясно, что исследование начинается с этапа асимптотики: чтобы сравнивать оценки, надо сначала их построить и быть уверенными, что они не являются абсурдными (такую уверенность дает доказательство состоятельности).

С какой оценки начинать? Одним из наиболее известных и простых в употреблении методов является метод моментов. Название связано с тем, что этот метод опирается на использование выборочных моментов

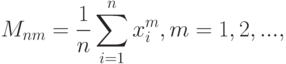
$M_{nm}=\frac{1}{n}\sum_{i=1}^n x_i^m,m=1,2,...,$

где 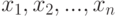x_1, x_2,...,x_n - выборка, т.е. набор независимых одинаково распределенных случайных величин с числовыми значениями.

В прикладной статистике метод анализа данных называется методом моментов, если он использует статистику

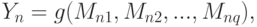$Y_n=g(M_{n1},M_{n2},...,M_{nq}),$

( 2)

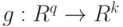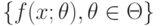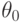где $g:R^q\rightarrow R^k$ - некоторая функция (здесь - число неизвестных числовых параметров). Чаще всего термин "метод моментов" используют, когда речь идет об оценивании параметров. В этом случае обычно предполагают, что плотность вероятности распределения элементов выборки f(x) входит в заранее известное статистику параметрическое семейство $\{f(x;\theta),\theta\in\Theta\}$ , т.е. $f(x)=f(x;\theta_0)$ при некотором $\theta_0$ . 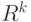Здесь $\Theta$ - заранее заданное -мерное пространство параметров, являющееся подмножеством евклидова пространства R^k , а конкретное значение параметра 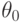$\theta_0$ статистику неизвестно, его и следует оценить. Известно также, что неизвестный параметр определяется с помощью известной статистику функции через начальные моменты элементов выборки:

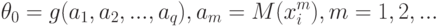$\theta_0=g(a_1,a_2,...,a_q),a_m=M(x_i^m),m=1,2,...$

( 3)

В методе моментов в качестве оценки 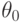$\theta_0$ используют статистику 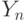Y_n вида (2), которая отличается от формулы (2) тем, что теоретические моменты заменены выборочными.

Статистики 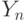Y_n вида (2) применяются не только для оценивания параметров, но и для непараметрического оценивания характеристик случайной величины, таких, как коэффициент вариации, и для проверки гипотез. Во всех случаях применения статистики 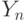Y_n вида (2) говорят о методе моментов.

Распределение вектора 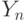Y_n во всех практически важных случаях является асимптотически нормальным. Это утверждение опирается на следующий общий факт.

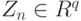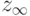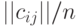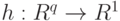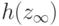Пусть случайный вектор $Z_n\in R^q$ асимптотически нормален с математическим ожиданием $z_{\infty}$ и ковариационной матрицей $||c_{ij}||/n$ , а функция $h:R^q\rightarrow R^1$ достаточно гладкая. Тогда случайная величина h(Z_n) асимптотически нормальна с математическим ожиданием $h(z_{\infty})$ и дисперсией

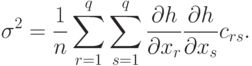$\sigma^2=\frac{1}{n} \sum_{r=1}^q\sum_{s=1}^q \frac{\partial h}{\partial x_r}\frac{\partial h}{\partial x_s}c_{rs}.$

( 4)

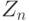Этот способ нахождения предельного распределения известен как $\delta$ -метод Рао [ [ 4.23 ] ], метод линеаризации [ [ 4.3 ] ]. Последний термин и будем использовать. Условия регулярности, накладываемые на распределение случайной величины Z_n и функцию , при которых метод линеаризации обоснован, хорошо известны (см. [ ], [ [ 6.2 ] , с.337-339], а также "Теоретическая база прикладной статистики" настоящего курса).

Дальше >>

Авторизоваться

Прикладная статистика

Оценивание

6.1. Методы оценивания параметров

Вопросы и ответы