|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Основы вероятностно-статистических методов описания неопределенностей
Введем понятие семейства нормальных распределений. По определению нормальным распределением называется распределение случайной величины  , для которой распределение приведенной случайной величины есть
, для которой распределение приведенной случайной величины есть 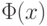 . Как следует из общих свойств масштабно-сдвиговых семейств распределений (см. выше), нормальное распределение – это распределение случайной величины
. Как следует из общих свойств масштабно-сдвиговых семейств распределений (см. выше), нормальное распределение – это распределение случайной величины
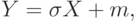
где  – случайная величина с распределением
– случайная величина с распределением 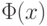 , причем
, причем 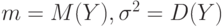 . Нормальное распределение с параметрами
. Нормальное распределение с параметрами  и
и  обычно обозначается
обычно обозначается 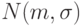 (иногда используется обозначение
(иногда используется обозначение 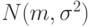 ).
).
Как следует из (8), плотность вероятности нормального распределения 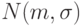 есть
есть
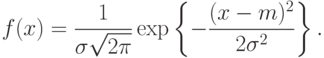
Нормальные распределения образуют масштабно-сдвиговое семейство. При этом параметром масштаба является 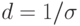 , а параметром сдвига
, а параметром сдвига 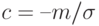 .
.
Для центральных моментов третьего и четвертого порядка нормального распределения справедливы равенства

Эти равенства лежат в основе классических методов проверки того, что результаты наблюдений подчиняются нормальному распределению. В настоящее время нормальность обычно рекомендуется проверять по критерию  Шапиро – Уилка. Проблема проверки нормальности обсуждается ниже.
Шапиро – Уилка. Проблема проверки нормальности обсуждается ниже.
Если случайные величины 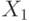 и
и  имеют функции распределения
имеют функции распределения 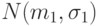 и
и  соответственно, то
соответственно, то  имеет распределение
имеет распределение  . Следовательно, если случайные величины
. Следовательно, если случайные величины 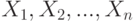 независимы и имеют одно и тоже распределение
независимы и имеют одно и тоже распределение 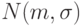 , то их среднее арифметическое
, то их среднее арифметическое
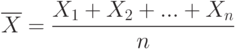
имеет распределение 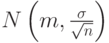 .. Эти свойства нормального распределения постоянно используются в различных вероятностно-статистических методах принятия решений, в частности, при статистическом регулировании технологических процессов и в статистическом приемочном контроле по количественному признаку.
.. Эти свойства нормального распределения постоянно используются в различных вероятностно-статистических методах принятия решений, в частности, при статистическом регулировании технологических процессов и в статистическом приемочном контроле по количественному признаку.
С помощью нормального распределения определяются три распределения, которые в настоящее время часто используются при статистической обработке данных.
Распределение 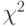 (хи – квадрат) – распределение случайной величины
(хи – квадрат) – распределение случайной величины

где случайные величины 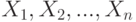 независимы и имеют одно и тоже распределение
независимы и имеют одно и тоже распределение 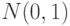 . При этом число слагаемых, т.е.
. При этом число слагаемых, т.е.  , называется "числом степеней свободы" распределения хи-квадрат.
, называется "числом степеней свободы" распределения хи-квадрат.
Распределение  Стьюдента – это распределение случайной величины
Стьюдента – это распределение случайной величины
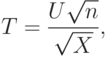
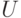 и
и  независимы,
независимы, 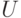 имеет распределение стандартное нормальное распределение
имеет распределение стандартное нормальное распределение 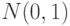 , а
, а  – распределение хи-квадрат с
– распределение хи-квадрат с  степенями свободы. При этом n называется "числом степеней свободы" распределения Стьюдента. Это распределение было введено в 1908 г. английским статистиком В. Госсетом, работавшем на фабрике, выпускающей пиво. Вероятностно-статистические методы использовались для принятия экономических и технических решений на этой фабрике, поэтому ее руководство запрещало В. Госсету публиковать научные статьи под своим именем. Таким способом охранялась коммерческая тайна, "ноу-хау" в виде вероятностно-статистических методов, разработанных В. Госсетом. Однако он имел возможность публиковаться под псевдонимом "Стьюдент".
История Госсета – Стьюдента показывает, что еще сто лет назад менеджерам Великобритании была очевидна большая экономическая эффективность вероятностно-статистических методов принятия решений.
степенями свободы. При этом n называется "числом степеней свободы" распределения Стьюдента. Это распределение было введено в 1908 г. английским статистиком В. Госсетом, работавшем на фабрике, выпускающей пиво. Вероятностно-статистические методы использовались для принятия экономических и технических решений на этой фабрике, поэтому ее руководство запрещало В. Госсету публиковать научные статьи под своим именем. Таким способом охранялась коммерческая тайна, "ноу-хау" в виде вероятностно-статистических методов, разработанных В. Госсетом. Однако он имел возможность публиковаться под псевдонимом "Стьюдент".
История Госсета – Стьюдента показывает, что еще сто лет назад менеджерам Великобритании была очевидна большая экономическая эффективность вероятностно-статистических методов принятия решений.Распределение Фишера – это распределение случайной величины
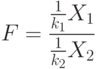
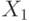 и
и  независимы и имеют распределения хи-квадрат с числом степеней свободы
независимы и имеют распределения хи-квадрат с числом степеней свободы 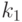 и
и  соответственно. При этом пара
соответственно. При этом пара 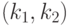 – пара "чисел степеней свободы" распределения Фишера, а именно:
– пара "чисел степеней свободы" распределения Фишера, а именно: 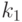 – число степеней свободы числителя, а
– число степеней свободы числителя, а  – число степеней свободы знаменателя. Распределение случайной величины
– число степеней свободы знаменателя. Распределение случайной величины  названо в честь великого английского статистика Р.Фишера (1890–1962), активно использовавшего его в своих работах.
названо в честь великого английского статистика Р.Фишера (1890–1962), активно использовавшего его в своих работах.Выражения для функций распределения хи-квадрат, Стьюдента и Фишера, их плотностей и характеристик, а также таблицы можно найти в специальной литературе (см., например, [ [ 2.1 ] ]).
Как уже отмечалось, нормальные распределения в настоящее время часто используют в вероятностных моделях в различных прикладных областях. В чем причина такой широкой распространенности этого двухпараметрического семейства распределений? Она проясняется следующей теоремой.
Центральная предельная теорема (для разнораспределенных слагаемых). Пусть 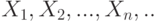 . – независимые случайные величины с математическими ожиданиями
. – независимые случайные величины с математическими ожиданиями  . и дисперсиями
. и дисперсиями 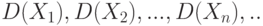 . соответственно. Пусть
. соответственно. Пусть
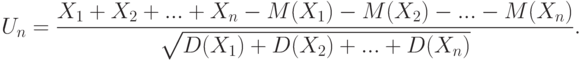
Тогда при справедливости некоторых условий, обеспечивающих малость вклада любого из слагаемых в 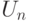 ,
,
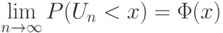
 .
.Условия, о которых идет речь, не будем здесь формулировать. Их можно найти в специальной литературе (см., например, [ [ 2.3 ] ]). "Выяснение условий, при которых действует ЦПТ, составляет заслугу выдающихся русских ученых А.А. Маркова (1857–1922) и, в особенности, А.М.Ляпунова (1857–1918)" [ [ 2.20 ] , с. 197].
Центральная предельная теорема показывает, что в случае, когда результат измерения (наблюдения) складывается под действием многих причин, причем каждая из них вносит лишь малый вклад, а совокупный итог определяется аддитивно, т.е. путем сложения, то распределение результата измерения (наблюдения) близко к нормальному.
Иногда считают, что для нормальности распределения достаточно того, что результат измерения (наблюдения)  формируется под действием многих причин, каждая из которых оказывает малое воздействие. Это не так. Важно, как эти причины действуют. Если аддитивно – то
формируется под действием многих причин, каждая из которых оказывает малое воздействие. Это не так. Важно, как эти причины действуют. Если аддитивно – то  имеет приближенно нормальное распределение. Если мультипликативно (т.е. действия отдельных причин перемножаются, а не складываются), то распределение
имеет приближенно нормальное распределение. Если мультипликативно (т.е. действия отдельных причин перемножаются, а не складываются), то распределение  близко не к нормальному, а к так называемому логарифмически нормальному, т.е. не
близко не к нормальному, а к так называемому логарифмически нормальному, т.е. не  , а
, а 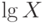 имеет приблизительно нормальное распределение. Если же нет оснований считать, что действует один из этих двух механизмов формирования итогового результата (или какой-либо иной вполне определенный механизм), то про распределение
имеет приблизительно нормальное распределение. Если же нет оснований считать, что действует один из этих двух механизмов формирования итогового результата (или какой-либо иной вполне определенный механизм), то про распределение  ничего определенного сказать нельзя.
ничего определенного сказать нельзя.
Из сказанного вытекает, что в конкретной прикладной задаче нормальность результатов измерений (наблюдений), как правило, нельзя установить из общих соображений, ее следует проверять с помощью статистических критериев. Или же использовать непараметрические статистические методы, не опирающиеся на предположения о принадлежности функций распределения результатов измерений (наблюдений) к тому или иному параметрическому семейству.
Непрерывные распределения, используемые в вероятностно-статистических методах принятия решений. Кроме масштабно-сдвигового семейства нормальных распределений, широко используют ряд других семейств распределения – логарифмически нормальных, экспоненциальных, Вейбулла-Гнеденко, гамма-распределений. Рассмотрим эти семейства.
Случайная величина  имеет логарифмически нормальное распределение, если случайная величина
имеет логарифмически нормальное распределение, если случайная величина 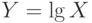 имеет нормальное распределение. Тогда
имеет нормальное распределение. Тогда  .
.  также имеет нормальное распределение
также имеет нормальное распределение 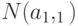 , где
, где 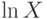 – натуральный логарифм
– натуральный логарифм  . Плотность логарифмически нормального распределения такова:
. Плотность логарифмически нормального распределения такова:
![f(x;a_1,\sigma_1)=
\left\{
\begin{aligned}
&\frac{1}{\sigma_1\sqrt{2\pi}x}\exp\left[-\frac{(\ln x-a_1)^2}{2\sigma_1^2}\right],\quad x>0,\\
&0, x\le 0.
\end{aligned}
\right..](/sites/default/files/tex_cache/9bf34044e0b4198ca8cb624b848c8754.png)
Из центральной предельной теоремы следует, что произведение 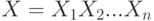 независимых положительных случайных величин
независимых положительных случайных величин 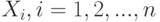 , при больших
, при больших  можно аппроксимировать логарифмически нормальным распределением. В частности, мультипликативная модель формирования заработной платы или дохода приводит к рекомендации приближать распределения заработной платы и дохода логарифмически нормальными законами. Для России эта рекомендация оказалась обоснованной – статистические данные подтверждают ее.
можно аппроксимировать логарифмически нормальным распределением. В частности, мультипликативная модель формирования заработной платы или дохода приводит к рекомендации приближать распределения заработной платы и дохода логарифмически нормальными законами. Для России эта рекомендация оказалась обоснованной – статистические данные подтверждают ее.
Имеются и другие вероятностные модели, приводящие к логарифмически нормальному закону. Классический пример такой модели дан А.Н. Колмогоровым [ [ 2.8 ] ], который из физически обоснованной системы постулатов вывел заключение о том, что размеры частиц при дроблении кусков руды, угля и т.п. на шаровых мельницах имеют логарифмически нормальное распределение.
Перейдем к другому семейству распределений, широко используемому в различных вероятностно-статистических методах принятия решений и других прикладных исследованиях, – семейству экспоненциальных распределений. Начнем с вероятностной модели, приводящей к таким распределениям. Для этого рассмотрим "поток событий", т.е. последовательность событий, происходящих одно за другим в какие-то моменты времени. Примерами могут служить потоки: вызовов на телефонной станции; отказов оборудования в технологической цепочке; отказов изделий при испытаниях продукции; обращений клиентов в отделение банка; покупателей, обращающихся за товарами и услугами, и т.д. В теории потоков событий справедлива теорема, аналогичная центральной предельной теореме, но в ней речь идет не о суммировании случайных величин, а о суммировании потоков событий.
Рассматривается суммарный поток, составленный из большого числа независимых потоков, ни один из которых не оказывает преобладающего влияния на суммарный поток. Например, поток вызовов, поступающих на телефонную станцию, слагается из большого числа независимых потоков вызовов, исходящих от отдельных абонентов. Доказано [
[
2.3
]
], что в случае, когда характеристики потоков не зависят от времени, суммарный поток полностью описывается одним числом 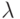 – интенсивностью потока. Для суммарного потока рассмотрим случайную величину
– интенсивностью потока. Для суммарного потока рассмотрим случайную величину  - длину промежутка времени между последовательными событиями. Ее функция распределения имеет вид
- длину промежутка времени между последовательными событиями. Ее функция распределения имеет вид
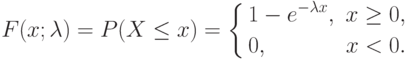 |
( 10) |
Это распределение называется экспоненциальным распределением, так как в формуле (10) участвует экспоненциальная функция 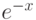 . Величина
. Величина 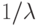 – масштабный параметр. Иногда вводят и параметр сдвига
– масштабный параметр. Иногда вводят и параметр сдвига  , экспоненциальным называют распределение случайной величины
, экспоненциальным называют распределение случайной величины 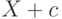 , где распределение
, где распределение  задается формулой (10).
задается формулой (10).
Экспоненциальные распределения – частный случай так называемых распределений Вейбулла-Гнеденко. Они названы по фамилиям инженера В. Вейбулла, введшего эти распределения в практику анализа результатов усталостных испытаний, и математика Б.В.Гнеденко (1912–1995), получившего такие распределения в качестве предельных при изучении максимального из результатов испытаний. Пусть  – случайная величина, характеризующая длительность функционирования изделия, сложной системы, элемента (т.е. ресурс, наработку до предельного состояния и т.п.), длительность функционирования предприятия или жизни живого существа и т.д. Важную роль играет интенсивность отказа
– случайная величина, характеризующая длительность функционирования изделия, сложной системы, элемента (т.е. ресурс, наработку до предельного состояния и т.п.), длительность функционирования предприятия или жизни живого существа и т.д. Важную роль играет интенсивность отказа
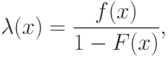 |
( 11) |
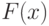 и
и  – функция распределения и плотность случайной величины
– функция распределения и плотность случайной величины  .
.Опишем типичное поведение интенсивности отказа. Весь интервал времени можно разбить на три периода. На первом из них функция  имеет высокие значения и явную тенденцию к убыванию (чаще всего она монотонно убывает). Это можно объяснить наличием в рассматриваемой партии единиц продукции с явными и скрытыми дефектами, которые приводят к относительно быстрому выходу из строя этих единиц продукции. Первый период называют "периодом приработки" (или "обкатки"). Именно на него обычно распространяется гарантийный срок.
имеет высокие значения и явную тенденцию к убыванию (чаще всего она монотонно убывает). Это можно объяснить наличием в рассматриваемой партии единиц продукции с явными и скрытыми дефектами, которые приводят к относительно быстрому выходу из строя этих единиц продукции. Первый период называют "периодом приработки" (или "обкатки"). Именно на него обычно распространяется гарантийный срок.
Затем наступает период нормальной эксплуатации, характеризующийся приблизительно постоянной и сравнительно низкой интенсивностью отказов. Природа отказов в этот период носит внезапный характер (аварии, ошибки эксплуатационных работников и т.п.) и не зависит от длительности эксплуатации единицы продукции.
Наконец, последний период эксплуатации – период старения и износа. Природа отказов в этот период – в необратимых физико-механических и химических изменениях материалов, приводящих к прогрессирующему ухудшению качества единицы продукции и окончательному выходу ее из строя.
Каждому периоду соответствует свой вид функции 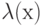 . Рассмотрим класс степенных зависимостей
. Рассмотрим класс степенных зависимостей
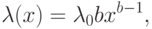 |
( 12) |
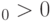 и
и 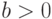 – некоторые числовые параметры. Значения
– некоторые числовые параметры. Значения 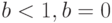 и
и 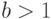 отвечают виду интенсивности отказов в периоды приработки, нормальной эксплуатации и старения соответственно.
отвечают виду интенсивности отказов в периоды приработки, нормальной эксплуатации и старения соответственно.Соотношение (12) при заданной интенсивности отказа 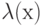 – дифференциальное уравнение относительно функции
– дифференциальное уравнение относительно функции 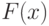 . Из теории дифференциальных уравнений следует, что
. Из теории дифференциальных уравнений следует, что
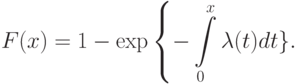 |
( 13) |
Подставив (12) в (13), получим, что
![F(x)=
\left\{
\begin{aligned}
1-\exp[-\lambda_0 x^b], x\ge 0, \\
0, x< 0.
\end{aligned}
\right.](/sites/default/files/tex_cache/da8a8cba020a984689c122eeb61b1a0a.png) |
( 14) |
Распределение, задаваемое формулой (14), называется распределением Вейбулла-Гнеденко. Поскольку
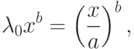
 |
( 15) |
 , задаваемая формулой (15), является масштабным параметром. Иногда вводят и параметр сдвига, т.е. функциями распределения Вейбулла-Гнеденко называют
, задаваемая формулой (15), является масштабным параметром. Иногда вводят и параметр сдвига, т.е. функциями распределения Вейбулла-Гнеденко называют 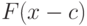 , где
, где 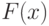 задается формулой (14) при некоторых
задается формулой (14) при некоторых 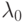 и
и  .
.Плотность распределения Вейбулла-Гнеденко имеет вид
![f(a;a,b,c)=
\left\{
\begin{gathered}
\frac{b}{a}
\left(
\frac{x-c}{a}
\right)^{b-1}
\exp
\left[
-\left(
\frac{x-c}{a}
\right)^b
\right], x\ge c, \\
0,\quad x<c,
\end{gathered}
\right.](/sites/default/files/tex_cache/ba3c6291eed5255fc3aa474928fe9d49.png) |
( 16) |
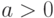 – параметр масштаба,
– параметр масштаба, 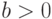 – параметр формы,
– параметр формы,  – параметр сдвига. При этом параметр
– параметр сдвига. При этом параметр  из формулы (16) связан с параметром
из формулы (16) связан с параметром 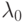 из формулы (14) соотношением, указанным в формуле (15).
из формулы (14) соотношением, указанным в формуле (15).Экспоненциальное распределение – весьма частный случай распределения Вейбулла-Гнеденко, соответствующий значению параметра формы 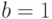 .
.
Распределение Вейбулла-Гнеденко применяется также при построении вероятностных моделей ситуаций, в которых поведение объекта определяется "наиболее слабым звеном". Подразумевается аналогия с цепью, сохранность которой определяется тем ее звеном, которое имеет наименьшую прочность. Другими словами, пусть 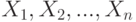 – независимые одинаково распределенные случайные величины,
– независимые одинаково распределенные случайные величины,
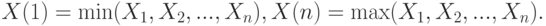
В ряде прикладных задач большую роль играют 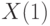 и
и 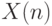 , в частности, при исследовании максимально возможных значений ("рекордов") тех или иных значений, например, страховых выплат или потерь из-за коммерческих рисков, при изучении пределов упругости и выносливости стали, ряда характеристик надежности и т.п. Показано, что при больших
, в частности, при исследовании максимально возможных значений ("рекордов") тех или иных значений, например, страховых выплат или потерь из-за коммерческих рисков, при изучении пределов упругости и выносливости стали, ряда характеристик надежности и т.п. Показано, что при больших  распределения
распределения 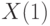 и
и 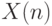 , как правило, хорошо описываются распределениями Вейбулла-Гнеденко. Основополагающий вклад в изучение распределений
, как правило, хорошо описываются распределениями Вейбулла-Гнеденко. Основополагающий вклад в изучение распределений 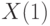 и
и 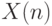 внес советский математик Б.В. Гнеденко. Использованию полученных результатов в экономике, менеджменте, технике и других областях посвящены труды В. Вейбулла, Э. Гумбеля, В.Б. Невзорова, Э.М. Кудлаева и других специалистов.
внес советский математик Б.В. Гнеденко. Использованию полученных результатов в экономике, менеджменте, технике и других областях посвящены труды В. Вейбулла, Э. Гумбеля, В.Б. Невзорова, Э.М. Кудлаева и других специалистов.
Перейдем к семейству гамма-распределений. Они широко применяются в экономике и менеджменте, теории и практике надежности и испытаний, в различных областях техники, метеорологии и т.д. В частности, гамма-распределению подчинены во многих ситуациях такие величины, как общий срок службы изделия, длина цепочки токопроводящих пылинок, время достижения изделием предельного состояния при коррозии, время наработки до  -го отказа,
-го отказа,  ., и т.д. Продолжительность жизни больных хроническими заболеваниями, время достижения определенного эффекта при лечении в ряде случаев имеют гамма-распределение. Это распределение наиболее адекватно для описания спроса в экономико-математических моделях управления запасами (логистики).
., и т.д. Продолжительность жизни больных хроническими заболеваниями, время достижения определенного эффекта при лечении в ряде случаев имеют гамма-распределение. Это распределение наиболее адекватно для описания спроса в экономико-математических моделях управления запасами (логистики).
Плотность гамма-распределения имеет вид
![f(x;a,b,c)=
\left\{
\begin{gathered}
\frac{1}{\Gamma(a)}(x-c)^{a-1}b^{-a}\exp
\left[
-\frac{x-c}{b}
\right], x\ge c, \\
0, \; x<c.
\end{gathered}
\right.](/sites/default/files/tex_cache/14afabac609417de3c872332f4dd258b.png) |
( 17) |
Плотность вероятности в формуле (17) определяется тремя параметрами 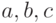 , где
, где 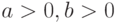 . При этом
. При этом  является параметром формы,
является параметром формы,  – параметром масштаба и
– параметром масштаба и  – параметром сдвига. Множитель
– параметром сдвига. Множитель 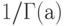 является нормировочным, он введен, чтобы
является нормировочным, он введен, чтобы
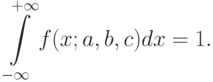
Здесь 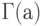 – одна из используемых в математике специальных функций, так называемая "гамма-функция", по которой названо и распределение, задаваемое формулой (17),
– одна из используемых в математике специальных функций, так называемая "гамма-функция", по которой названо и распределение, задаваемое формулой (17),
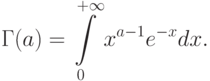
При фиксированном  формула (17) задает масштабно-сдвиговое семейство распределений, порождаемое распределением с плотностью
формула (17) задает масштабно-сдвиговое семейство распределений, порождаемое распределением с плотностью
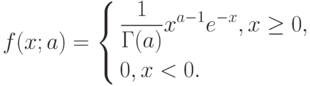 |
( 18) |
Распределение вида (18) называется стандартным гамма-распределением. Оно получается из формулы (17) при 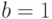 и
и 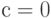 .
.
Частным случаем гамма-распределений при 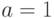 являются экспоненциальные распределения (с
являются экспоненциальные распределения (с 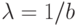 ). При натуральном
). При натуральном  и
и 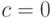 гамма-распределения называются распределениями Эрланга. С работ датского ученого К.А. Эрланга (1878–1929), сотрудника Копенгагенской телефонной компании, изучавшего в 1908–1922 гг. функционирование телефонных сетей, началось развитие теории массового обслуживания. Эта теория занимается вероятностно-статистическим моделированием систем, в которых происходит обслуживание потока заявок, с целью принятия оптимальных решений. Распределения Эрланга используют в тех же прикладных областях, в которых применяют экспоненциальные распределения.
Это основано на следующем математическом факте: сумма
гамма-распределения называются распределениями Эрланга. С работ датского ученого К.А. Эрланга (1878–1929), сотрудника Копенгагенской телефонной компании, изучавшего в 1908–1922 гг. функционирование телефонных сетей, началось развитие теории массового обслуживания. Эта теория занимается вероятностно-статистическим моделированием систем, в которых происходит обслуживание потока заявок, с целью принятия оптимальных решений. Распределения Эрланга используют в тех же прикладных областях, в которых применяют экспоненциальные распределения.
Это основано на следующем математическом факте: сумма  независимых случайных величин, экспоненциально распределенных с одинаковыми параметрами
независимых случайных величин, экспоненциально распределенных с одинаковыми параметрами 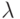 и
и  , имеет гамма-распределение с параметром формы
, имеет гамма-распределение с параметром формы 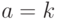 , параметром масштаба
, параметром масштаба  и параметром сдвига
и параметром сдвига  . При
. При 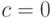 получаем распределение Эрланга.
получаем распределение Эрланга.
Если случайная величина  имеет гамма-распределение с параметром формы
имеет гамма-распределение с параметром формы  таким, что
таким, что 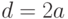 - целое число,
- целое число,  и
и 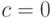 , то
, то 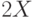 имеет распределение хи-квадрат с
имеет распределение хи-квадрат с 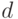 степенями свободы.
степенями свободы.
Случайная величина  с гамма-распределением имеет следующие характеристики:
с гамма-распределением имеет следующие характеристики:
Нормальное распределение – предельный случай гамма-распределения. Точнее, пусть 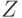 – случайная величина, имеющая стандартное гамма-распределение, заданное формулой (18). Тогда
– случайная величина, имеющая стандартное гамма-распределение, заданное формулой (18). Тогда
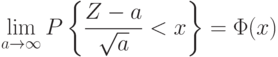
 , где
, где 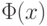 – функция стандартного нормального распределения
– функция стандартного нормального распределения 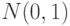 .
.В прикладных исследованиях используются и другие параметрические семейства распределений, из которых наиболее известны система кривых Пирсона, ряды Эджворта и Шарлье. Здесь они не рассматриваются.
Дискретные распределения, используемые в вероятностно-статистических методах принятия решений. Наиболее часто используют три семейства дискретных распределений – биномиальных, гипергеометрических и Пуассона, а также некоторые другие – геометрических, отрицательных биномиальных, мультиномиальных, отрицательных гипергеометрических и т.д.
Как уже говорилось, биномиальное распределение имеет место при независимых испытаниях, в каждом из которых с вероятностью  появляется событие
появляется событие  . Если общее число испытаний
. Если общее число испытаний  задано, то число испытаний
задано, то число испытаний  , в которых появилось событие
, в которых появилось событие  , имеет биномиальное распределение. Для биномиального распределения вероятность принятия случайной величиной
, имеет биномиальное распределение. Для биномиального распределения вероятность принятия случайной величиной  значения
значения  определяется формулой
определяется формулой
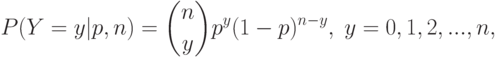 |
( 19) |
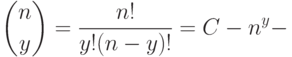
 элементов по
элементов по  , известное из комбинаторики. Для всех
, известное из комбинаторики. Для всех  , кроме
, кроме 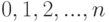 , имеем
, имеем 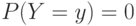 . Биномиальное распределение при фиксированном объеме выборки
. Биномиальное распределение при фиксированном объеме выборки  задается параметром
задается параметром  , т.е. биномиальные распределения образуют однопараметрическое семейство. Они применяются при анализе данных выборочных исследований [
[
2.16
]
], в частности, при изучении предпочтений потребителей, выборочном контроле качества продукции по планам одноступенчатого контроля, при испытаниях совокупностей индивидуумов в демографии, социологии, медицине, биологии и др.
, т.е. биномиальные распределения образуют однопараметрическое семейство. Они применяются при анализе данных выборочных исследований [
[
2.16
]
], в частности, при изучении предпочтений потребителей, выборочном контроле качества продукции по планам одноступенчатого контроля, при испытаниях совокупностей индивидуумов в демографии, социологии, медицине, биологии и др.Если 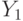 и
и 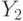 - независимые биномиальные случайные величины с одним и тем же параметром
- независимые биномиальные случайные величины с одним и тем же параметром  , определенные по выборкам с объемами
, определенные по выборкам с объемами 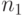 и
и 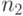 соответственно, то
соответственно, то  - биномиальная случайная величина, имеющая распределение (19) с
- биномиальная случайная величина, имеющая распределение (19) с 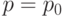 и
и 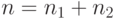 . Это замечание расширяет область применимости биномиального распределения, позволяя объединять результаты нескольких групп испытаний, когда есть основания полагать, что всем этим группам соответствует один и тот же параметр.
. Это замечание расширяет область применимости биномиального распределения, позволяя объединять результаты нескольких групп испытаний, когда есть основания полагать, что всем этим группам соответствует один и тот же параметр.
Характеристики биномиального распределения вычислены ранее:
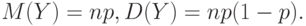
В  2.2 (События и вероятности) для биномиальной случайной величины доказан закон больших чисел:
2.2 (События и вероятности) для биномиальной случайной величины доказан закон больших чисел:
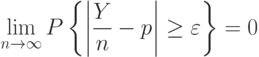
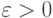 . С помощью центральной предельной теоремы закон больших чисел можно уточнить, указав, насколько
. С помощью центральной предельной теоремы закон больших чисел можно уточнить, указав, насколько 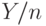 отличается от
отличается от  .
.Теорема Муавра-Лапласа. Для любых чисел  и
и  ,
,  , имеем
, имеем
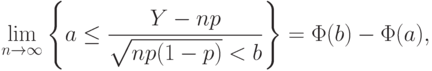
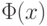 - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.Для доказательства достаточно воспользоваться представлением  в виде суммы независимых случайных величин, соответствующих исходам отдельных испытаний, формулами для
в виде суммы независимых случайных величин, соответствующих исходам отдельных испытаний, формулами для 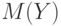 и
и 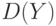 и центральной предельной теоремой.
и центральной предельной теоремой.
Эта теорема для случая 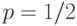 доказана английским математиком А. Муавром (1667-1754) в 1730 г. В приведенной выше формулировке она была доказана в 1810 г. французским математиком Пьером Симоном Лапласом (1749 - 1827).
доказана английским математиком А. Муавром (1667-1754) в 1730 г. В приведенной выше формулировке она была доказана в 1810 г. французским математиком Пьером Симоном Лапласом (1749 - 1827).
Гипергеометрическое распределение имеет место при выборочном контроле конечной совокупности объектов объема 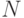 по альтернативному признаку. Каждый контролируемый объект классифицируется либо как обладающий признаком
по альтернативному признаку. Каждый контролируемый объект классифицируется либо как обладающий признаком  , либо как не обладающий этим признаком. Гипергеометрическое распределение имеет случайная величина
, либо как не обладающий этим признаком. Гипергеометрическое распределение имеет случайная величина  , равная числу объектов, обладающих признаком
, равная числу объектов, обладающих признаком  в случайной выборке объема
в случайной выборке объема  , где
, где  . Например, число
. Например, число  дефектных единиц продукции в случайной выборке объема
дефектных единиц продукции в случайной выборке объема  из партии объема
из партии объема 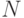 имеет гипергеометрическое распределение, если
имеет гипергеометрическое распределение, если  . Другой пример - лотерея. Пусть признак
. Другой пример - лотерея. Пусть признак  билета - это признак "быть выигрышным". Пусть всего билетов
билета - это признак "быть выигрышным". Пусть всего билетов 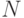 , а некоторое лицо приобрело
, а некоторое лицо приобрело  из них. Тогда число выигрышных билетов у этого лица имеет гипергеометрическое распределение.
из них. Тогда число выигрышных билетов у этого лица имеет гипергеометрическое распределение.
Для гипергеометрического распределения вероятность принятия случайной величиной  значения y имеет вид
значения y имеет вид
 |
( 20) |
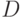 - число объектов, обладающих признаком
- число объектов, обладающих признаком  , в рассматриваемой совокупности объема
, в рассматриваемой совокупности объема 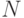 . При этом
. При этом  принимает значения от
принимает значения от  до
до 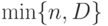 , при прочих y вероятность в формуле (20) равна 0. Таким образом, гипергеометрическое распределение определяется тремя параметрами - объемом генеральной совокупности
, при прочих y вероятность в формуле (20) равна 0. Таким образом, гипергеометрическое распределение определяется тремя параметрами - объемом генеральной совокупности 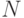 , числом объектов
, числом объектов 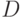 в ней, обладающих рассматриваемым признаком
в ней, обладающих рассматриваемым признаком  , и объемом выборки
, и объемом выборки  .
.Простой случайной выборкой объема  из совокупности объема
из совокупности объема 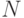 называется выборка, полученная в результате случайного отбора, при котором любой из
называется выборка, полученная в результате случайного отбора, при котором любой из  наборов из
наборов из  объектов имеет одну и ту же вероятность быть отобранным. Методы случайного отбора выборок респондентов (опрашиваемых) или единиц штучной продукции рассматриваются в инструктивно-методических и нормативно-технических документах. Один из методов отбора таков: объекты отбирают один из другим, причем на каждом шаге каждый из оставшихся в совокупности объектов имеет одинаковые шансы быть отобранным. В литературе для рассматриваемого типа выборок используются также термины "случайная выборка", "случайная выборка без возвращения".
объектов имеет одну и ту же вероятность быть отобранным. Методы случайного отбора выборок респондентов (опрашиваемых) или единиц штучной продукции рассматриваются в инструктивно-методических и нормативно-технических документах. Один из методов отбора таков: объекты отбирают один из другим, причем на каждом шаге каждый из оставшихся в совокупности объектов имеет одинаковые шансы быть отобранным. В литературе для рассматриваемого типа выборок используются также термины "случайная выборка", "случайная выборка без возвращения".
Поскольку объемы генеральной совокупности (партии) 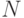 и выборки
и выборки  обычно известны, то подлежащим оцениванию параметром гипергеометрического распределения является
обычно известны, то подлежащим оцениванию параметром гипергеометрического распределения является 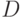 . В статистических методах управления качеством продукции
. В статистических методах управления качеством продукции 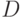 - обычно число дефектных единиц продукции в партии. Представляет интерес также характеристика распределения
- обычно число дефектных единиц продукции в партии. Представляет интерес также характеристика распределения 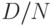 - уровень дефектности.
- уровень дефектности.
Для гипергеометрического распределения
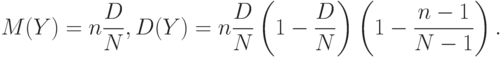
Последний множитель в выражении для дисперсии близок к 1, если 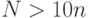 . Если при этом сделать замену
. Если при этом сделать замену 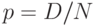 , то выражения для математического ожидания и дисперсии гипергеометрического распределения перейдут в выражения для математического ожидания и дисперсии биномиального распределения. Это не случайно. Можно показать, что
, то выражения для математического ожидания и дисперсии гипергеометрического распределения перейдут в выражения для математического ожидания и дисперсии биномиального распределения. Это не случайно. Можно показать, что
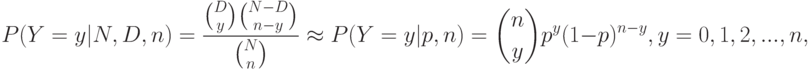
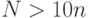 , где
, где 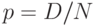 . Справедливо предельное соотношение
. Справедливо предельное соотношение
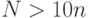 .
.Третье широко используемое дискретное распределение - распределение Пуассона. Случайная величина  имеет распределение Пуассона, если
имеет распределение Пуассона, если

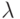 - параметр распределения Пуассона, и
- параметр распределения Пуассона, и 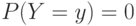 для всех прочих
для всех прочих  (при
(при  обозначено
обозначено 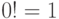 ). Для распределения Пуассона
). Для распределения Пуассона
Это распределение названо в честь французского математика С.Д.Пуассона (1781-1840), впервые получившего его в 1837 г. Распределение Пуассона является предельным случаем биномиального распределения, когда вероятность  осуществления события мала, но число испытаний
осуществления события мала, но число испытаний  велико, причем
велико, причем 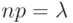 . Точнее, справедливо предельное соотношение
. Точнее, справедливо предельное соотношение
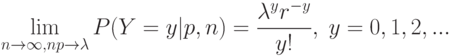
Поэтому распределение Пуассона (в старой терминологии "закон распределения") часто называют также "законом редких событий".
Распределение Пуассона возникает в теории потоков событий (см. выше). Доказано, что для простейшего потока с постоянной интенсивностью  число событий (вызовов), происшедших за время
число событий (вызовов), происшедших за время  , имеет распределение Пуассона с параметром
, имеет распределение Пуассона с параметром 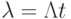 . Следовательно, вероятность того, что за время
. Следовательно, вероятность того, что за время  не произойдет ни одного события, равна
не произойдет ни одного события, равна 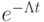 , т.е. функция распределения длины промежутка между событиями является экспоненциальной.
, т.е. функция распределения длины промежутка между событиями является экспоненциальной.
Распределение Пуассона используется при анализе результатов выборочных маркетинговых обследований потребителей, расчете оперативных характеристик планов статистического приемочного контроля в случае малых значений приемочного уровня дефектности, для описания числа разладок статистически управляемого технологического процесса в единицу времени, числа "требований на обслуживание", поступающих в единицу времени в систему массового обслуживания, статистических закономерностей несчастных случаев и редких заболеваний, и т.д.
Описание иных параметрических семейств дискретных распределений и возможности их практического использования рассматриваются в литературе.

 ,
,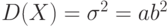 ,
,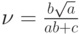 ,
,![M[(X-M(X))^3]=\frac{2}{\sqrt{a}}](/sites/default/files/tex_cache/eee765bfd5c5eb1561b7b780121071a2.png) ,
,![\frac{M[(X-M(X))^4]}{\sigma^4}-3=\frac{6}{a}](/sites/default/files/tex_cache/4e5feb3d59950c97029c0e091634857f.png) .
.