|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Основы вероятностно-статистических методов описания неопределенностей
Понятие эффективности вводится для несмещенных оценок, для которых 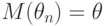 для всех возможных значений параметра
для всех возможных значений параметра  . Если не требовать несмещенности, то можно указать оценки, при некоторых
. Если не требовать несмещенности, то можно указать оценки, при некоторых  имеющие меньшую дисперсию и средний квадрат ошибки, чем эффективные.
имеющие меньшую дисперсию и средний квадрат ошибки, чем эффективные.
Пример 8. Рассмотрим "оценку" математического ожидания 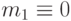 . Тогда
. Тогда 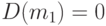 , т.е. всегда меньше дисперсии
, т.е. всегда меньше дисперсии  эффективной оценки
эффективной оценки  . Математическое ожидание среднего квадрата ошибки
. Математическое ожидание среднего квадрата ошибки 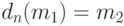 , т.е. при
, т.е. при 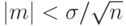 имеем
имеем 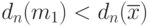 . Ясно, однако, что статистику
. Ясно, однако, что статистику 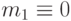 бессмысленно рассматривать в качестве оценки математического ожидания
бессмысленно рассматривать в качестве оценки математического ожидания  .
.
Пример 9. Более интересный пример рассмотрен американским математиком Дж. Ходжесом:
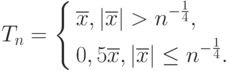
Ясно, что 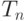 - состоятельная, асимптотически несмещенная оценка математического ожидания
- состоятельная, асимптотически несмещенная оценка математического ожидания  , при этом, как нетрудно вычислить,
, при этом, как нетрудно вычислить,
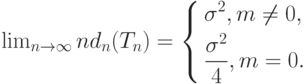
Последняя формула показывает, что при  оценка
оценка 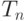 не хуже
не хуже  (при сравнении по среднему квадрату ошибки
(при сравнении по среднему квадрату ошибки  ), а при
), а при  - в четыре раза лучше.
- в четыре раза лучше.
Подавляющее большинство оценок 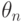 , используемых в вероятностно-статистических методах принятия решений, являются асимптотически нормальными, т.е. для них справедливы предельные соотношения:
, используемых в вероятностно-статистических методах принятия решений, являются асимптотически нормальными, т.е. для них справедливы предельные соотношения:
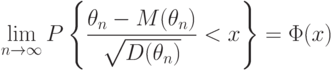
 , где
, где  - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Это означает, что для больших объемов выборок (практически - несколько десятков или сотен наблюдений) распределения оценок полностью описываются их математическими ожиданиями и дисперсиями, а качество оценок - значениями средних квадратов ошибок
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Это означает, что для больших объемов выборок (практически - несколько десятков или сотен наблюдений) распределения оценок полностью описываются их математическими ожиданиями и дисперсиями, а качество оценок - значениями средних квадратов ошибок 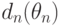 .
.Наилучшими асимптотически нормальными оценками, сокращенно НАН-оценками, называются те, для которых средний квадрат ошибки 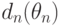 принимает при больших объемах выборки наименьшее возможное значение, т.е. величина
принимает при больших объемах выборки наименьшее возможное значение, т.е. величина  в формуле (4) минимальна. Ряд видов оценок - так называемые одношаговые оценки и оценки максимального правдоподобия - являются НАН-оценками, именно они обычно используются в вероятностно-статистических методах принятия решений.
в формуле (4) минимальна. Ряд видов оценок - так называемые одношаговые оценки и оценки максимального правдоподобия - являются НАН-оценками, именно они обычно используются в вероятностно-статистических методах принятия решений.
Какова точность оценки параметра? В каких границах он может лежать? В нормативно-технической и инструктивно-методической документации, в таблицах и программных продуктах наряду с алгоритмами расчетов точечных оценок даются правила нахождения доверительных границ. Они и указывают точность точечной оценки. При этом используются такие термины, как доверительная вероятность, доверительный интервал. Если речь идет об оценивании нескольких числовых параметров, или же функции, упорядочения и т.п., то говорят об оценивании с помощью доверительной области.
Доверительная область - это область в пространстве параметров, в которую с заданной вероятностью входит неизвестное значение оцениваемого параметра распределения. "Заданная вероятность" называется доверительной вероятностью и обычно обозначается  . Пусть
. Пусть  - пространство параметров. Рассмотрим статистику
- пространство параметров. Рассмотрим статистику 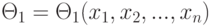 - функцию от результатов наблюдений
- функцию от результатов наблюдений 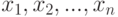 , значениями которой являются подмножества пространства параметров
, значениями которой являются подмножества пространства параметров  . Так как результаты наблюдений - случайные величины, то
. Так как результаты наблюдений - случайные величины, то 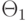 - также случайная величина, значения которой - подмножества множества
- также случайная величина, значения которой - подмножества множества  , т.е.
, т.е. 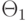 - случайное множество. Напомним, что множество - один из видов объектов нечисловой природы, случайные множества изучают в теории вероятностей и статистике объектов нечисловой природы.
- случайное множество. Напомним, что множество - один из видов объектов нечисловой природы, случайные множества изучают в теории вероятностей и статистике объектов нечисловой природы.
В ряде литературных источников, к настоящему времени во многом устаревших, под случайными величинами понимают только те из них, которые в качестве значений принимают действительные числа. Согласно справочнику академика РАН Ю.В.Прохорова и проф. Ю.А.Розанова [ [ 2.17 ] ] случайные величины могут принимать значения из любого множества. Так, случайные вектора, случайные функции, случайные множества, случайные ранжировки (упорядочения) - это отдельные виды случайных величин. Используется и иная терминология: термин "случайная величина" сохраняется только за числовыми функциями, определенными на пространстве элементарных событий, а в случае иных областей значений используется термин "случайный элемент". (Замечание для математиков: все рассматриваемые функции, определенные на пространстве элементарных событий, предполагаются измеримыми.)
Статистика 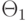 называется доверительной областью, соответствующей доверительной вероятности
называется доверительной областью, соответствующей доверительной вероятности  , если
, если
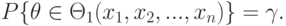 |
( 5) |
Ясно, что этому условию удовлетворяет, как правило, не одна, а много доверительных областей. Из них выбирают для практического применения какую-либо одну, исходя из дополнительных соображений, например, из соображений симметрии или минимизируя объем доверительной области, т.е. меру множества 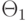 .
.
При оценке одного числового параметра в качестве доверительных областей обычно применяют доверительные интервалы (в том числе лучи), а не иные типа подмножеств прямой. Более того, для многих двухпараметрических и трехпараметрических распределений (нормальных, логарифмически нормальных, Вейбулла-Гнеденко, гамма-распределений и др.) обычно используют точечные оценки и построенные на их основе доверительные границы для каждого из двух или трех параметров отдельно. Это делают для удобства пользования результатами расчетов: доверительные интервалы легче применять, чем фигуры на плоскости или тела в трехмерном пространстве.
Как следует из сказанного выше, доверительный интервал - это интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения. Границы доверительного интервала называют доверительными границами. Доверительная вероятность  - вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным. Оцениванием с помощью доверительного интервала называют способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала.
- вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным. Оцениванием с помощью доверительного интервала называют способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала.
Для числового параметра  рассматривают верхнюю доверительную границу
рассматривают верхнюю доверительную границу 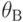 , нижнюю доверительную границу
, нижнюю доверительную границу  и двусторонние доверительные границы - верхнюю
и двусторонние доверительные границы - верхнюю 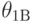 и нижнюю
и нижнюю 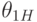 . Все четыре доверительные границы - функции от результатов наблюдений
. Все четыре доверительные границы - функции от результатов наблюдений 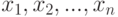 и доверительной вероятности
и доверительной вероятности  .
.
Верхняя доверительная граница 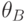 - случайная величина
- случайная величина 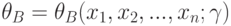 , для которой
, для которой  , где
, где  - истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид
- истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид ![(-\infty; \theta_B]](/sites/default/files/tex_cache/52fd8daeb51c81bc6abdf5d484693528.png) .
.
Нижняя доверительная граница  - случайная величина
- случайная величина 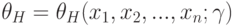 , для которой
, для которой 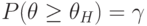 , где
, где  - истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид
- истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид  .
.
Двусторонние доверительные границы - верхняя 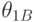 и нижняя
и нижняя 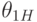 - это случайные величины
- это случайные величины 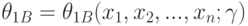 и
и 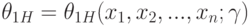 , такие, что
, такие, что 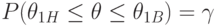 , где
, где  - истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид
- истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид ![[\theta_{1H}; \theta_{1B}]](/sites/default/files/tex_cache/4ac8e63772fc4eb18de14097745dd4ed.png) .
.
Вероятности, связанные с доверительными границами, можно записать в виде частных случаев формулы (5):
![P\{\theta\in(-\infty;\theta_B]\}=\gamma,P\{\theta\in[\theta_H;+\infty)\}
=\gamma,P\{\theta\in[\theta_{1H};\theta_{1B}]\}=\gamma.](/sites/default/files/tex_cache/1d804fd67b85c59c7dadb8b2a01bbd84.png)
В нормативно-технической и инструктивно-методической документации, научной и учебной литературе используют два типа правил определения доверительных границ - построенных на основе точного распределения и построенных на основе асимптотического распределения некоторой точечной оценки 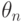 параметра
параметра  . Рассмотрим примеры.
. Рассмотрим примеры.
 . Пусть
. Пусть 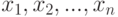 - выборка из нормального закона
- выборка из нормального закона 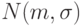 , параметры
, параметры  и
и  неизвестны. Укажем доверительные границы для
неизвестны. Укажем доверительные границы для  .
.
Известно [ [ 2.10 ] ], что случайная величина
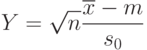
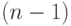 степенью свободы, где
степенью свободы, где  - выборочное среднее арифметическое и
- выборочное среднее арифметическое и  - выборочное среднее квадратическое отклонение. Пусть
- выборочное среднее квадратическое отклонение. Пусть 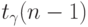 и
и 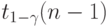 - квантили указанного распределения порядка
- квантили указанного распределения порядка  и
и 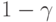 соответственно. Тогда
соответственно. Тогда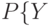
Следовательно,
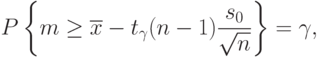
 , соответствующей доверительной вероятности
, соответствующей доверительной вероятности  , следует взять
, следует взять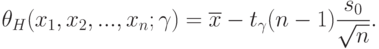 |
( 6) |
Аналогично получаем, что
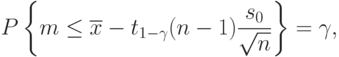
Поскольку распределение Стьюдента симметрично относительно 0, то  . Следовательно, в качестве верхней доверительной границы
. Следовательно, в качестве верхней доверительной границы 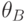 для
для  , соответствующей доверительной вероятности
, соответствующей доверительной вероятности  , следует взять
, следует взять
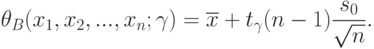 |
( 7) |
Как построить двусторонние доверительные границы? Положим
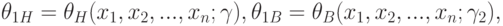
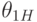 и
и 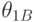 заданы формулами (6) и (7) соответственно. Поскольку неравенство
заданы формулами (6) и (7) соответственно. Поскольку неравенство  выполнено тогда и только тогда, когда
выполнено тогда и только тогда, когда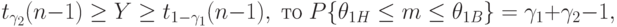
 ). Следовательно, если
). Следовательно, если 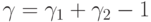 , то
, то 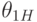 и
и 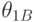 - двусторонние доверительные границы для
- двусторонние доверительные границы для  , соответствующие доверительной вероятности
, соответствующие доверительной вероятности  . Обычно полагают
. Обычно полагают  , т.е. в качестве двусторонних доверительных границ
, т.е. в качестве двусторонних доверительных границ 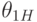 и
и 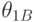 , соответствующих доверительной вероятности
, соответствующих доверительной вероятности  , используют односторонние доверительные границы
, используют односторонние доверительные границы  и
и 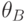 , соответствующие доверительной вероятности
, соответствующие доверительной вероятности  .
.Другой вид правил построения доверительных границ для параметра  основан на асимптотической нормальности некоторой точечной оценки
основан на асимптотической нормальности некоторой точечной оценки 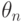 этого параметра. В вероятностно-статистических методах принятия решений используют, как уже отмечалось, несмещенные или асимптотически несмещенные оценки
этого параметра. В вероятностно-статистических методах принятия решений используют, как уже отмечалось, несмещенные или асимптотически несмещенные оценки 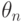 , для которых смещение либо равно 0, либо при больших объемах выборки пренебрежимо мало по сравнению со средним квадратическим отклонением оценки
, для которых смещение либо равно 0, либо при больших объемах выборки пренебрежимо мало по сравнению со средним квадратическим отклонением оценки 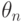 . Для таких оценок при всех
. Для таких оценок при всех 

 - функция нормального распределения
- функция нормального распределения  . Пусть
. Пусть 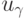 - квантиль порядка
- квантиль порядка  распределения
распределения  . Тогда
. Тогда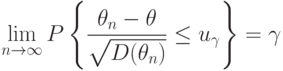 |
( 8) |
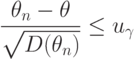

 можно было бы взять левую часть последнего неравенства. Однако точное значение дисперсии
можно было бы взять левую часть последнего неравенства. Однако точное значение дисперсии 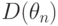 обычно неизвестно. Зато часто удается доказать, что дисперсия оценки имеет вид
обычно неизвестно. Зато часто удается доказать, что дисперсия оценки имеет вид
 слагаемых), где
слагаемых), где 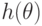 - некоторая функция от неизвестного параметра
- некоторая функция от неизвестного параметра  . Справедлива (см. 4.3) теорема о наследовании сходимости [
. Справедлива (см. 4.3) теорема о наследовании сходимости [  ,
,  2.4], согласно которой при подстановке в
2.4], согласно которой при подстановке в 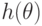 оценки
оценки 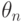 вместо
вместо  соотношение (8) остается справедливым, т.е.
соотношение (8) остается справедливым, т.е.
Следовательно, в качестве приближенной нижней доверительной границы следует взять
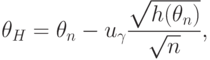
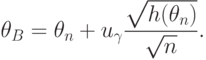
С ростом объема выборки качество приближенных доверительных границ улучшается, так как вероятности событий 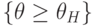 и
и 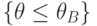 стремятся к
стремятся к  . Для построения двусторонних доверительных границ поступают аналогично правилу, указанному выше в примере 10 для интервального оценивания параметра
. Для построения двусторонних доверительных границ поступают аналогично правилу, указанному выше в примере 10 для интервального оценивания параметра  нормального распределения. А именно, используют односторонние доверительные границы, соответствующие доверительной вероятности
нормального распределения. А именно, используют односторонние доверительные границы, соответствующие доверительной вероятности  .
.
При обработке экономических, управленческих или технических статистических данных обычно используют значение доверительной вероятности  . Применяют также значения
. Применяют также значения 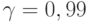 или
или 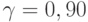 . Иногда встречаются значения
. Иногда встречаются значения 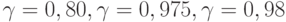 и др.
и др.
Для дискретных распределений, таких, как биномиальное, гипергеометрическое или распределение Пуассона (а также распределения статистики Колмогорова

 , например,
, например,  , нельзя указать доверительные границы, поскольку уравнения, с помощью которых вводятся доверительные границы, не имеют ни одного решения. Так, рассмотрим биномиальное распределение
, нельзя указать доверительные границы, поскольку уравнения, с помощью которых вводятся доверительные границы, не имеют ни одного решения. Так, рассмотрим биномиальное распределение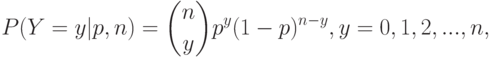
 - число осуществлений события,
- число осуществлений события,  - объем выборки. Для него нельзя указать статистику
- объем выборки. Для него нельзя указать статистику 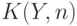 такую, что
такую, что
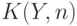 - функция от
- функция от  и может принимать не больше значений, чем принимает
и может принимать не больше значений, чем принимает  , т.е.
, т.е.  , а для
, а для  имеется бесконечно много возможных значений - столько, сколько точек на отрезке. Сказанное означает, что верхней доверительной границы в случае биномиального распределения не существует.
имеется бесконечно много возможных значений - столько, сколько точек на отрезке. Сказанное означает, что верхней доверительной границы в случае биномиального распределения не существует.Для дискретных распределений приходится изменить определения доверительных границ. Покажем изменения на примере биномиального распределения. Так, в качестве верхней доверительной границы 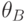 используют наименьшее
используют наименьшее 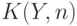 такое, что
такое, что
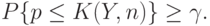
Аналогичным образом поступают для других доверительных границ и других распределений. Необходимо иметь в виду, что при небольших  и
и  истинная доверительная вероятность
истинная доверительная вероятность 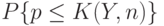 может существенно отличаться от номинальной
может существенно отличаться от номинальной  , как это подробно продемонстрировано в работе [
[
2.4
]
]. Поэтому наряду с величинами типа
, как это подробно продемонстрировано в работе [
[
2.4
]
]. Поэтому наряду с величинами типа 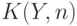 (т.е. доверительных границ) при разработке таблиц и компьютерных программ необходимо предусматривать возможность получения и величин типа
(т.е. доверительных границ) при разработке таблиц и компьютерных программ необходимо предусматривать возможность получения и величин типа 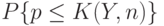 (т.е. достигаемых доверительных вероятностей).
(т.е. достигаемых доверительных вероятностей).
Основные понятия, используемые при проверке гипотез. Статистическая гипотеза - любое предположение, касающееся неизвестного распределения случайных величин (элементов). Приведем формулировки нескольких статистических гипотез:
- Результаты наблюдений имеют нормальное распределение с нулевым математическим ожиданием.
- Результаты наблюдений имеют функцию распределения
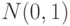 .
. - Результаты наблюдений имеют нормальное распределение.
- Результаты наблюдений в двух независимых выборках имеют одно и то же нормальное распределение.
- Результаты наблюдений в двух независимых выборках имеют одно и то же распределение.
Различают нулевую и альтернативную гипотезы. Нулевая - гипотеза, подлежащая проверке. Альтернативная - каждая допустимая гипотеза, отличная от нулевой. Нулевую гипотезу обозначают  , альтернативную -
, альтернативную -  (от англ. Hypothesis - "гипотеза").
(от англ. Hypothesis - "гипотеза").
Выбор тех или иных нулевых или альтернативных гипотез определяется стоящими перед менеджером, экономистом, инженером, исследователем прикладными задачами. Рассмотрим примеры.
Пример 11. Пусть нулевая гипотеза - гипотеза 2 из приведенного выше списка, а альтернативная - гипотеза 1. Сказанное означает, что реальная ситуация описывается вероятностной моделью, согласно которой результаты наблюдений рассматриваются как реализации независимых одинаково распределенных случайных величин с функцией распределения 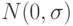 , где параметр
, где параметр  неизвестен статистику. В рамках этой модели нулевую гипотезу записывают так:
неизвестен статистику. В рамках этой модели нулевую гипотезу записывают так:

Пример 12. Пусть нулевая гипотеза - по-прежнему гипотеза 2 из приведенного выше списка, а альтернативная - гипотеза 3 из того же списка. Тогда в вероятностной модели управленческой, экономической или производственной ситуации предполагается, что результаты наблюдений образуют выборку из нормального распределения 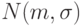 при некоторых значениях
при некоторых значениях  и
и  . Гипотезы записываются так:
. Гипотезы записываются так:
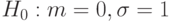
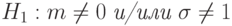 (т.е. либо
(т.е. либо  , либо
, либо 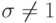 , либо и
, либо и  , и
, и 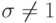 ).
).
Пример 13. Пусть  - гипотеза 1 из приведенного выше списка, а
- гипотеза 1 из приведенного выше списка, а  - гипотеза 3 из того же списка. Тогда вероятностная модель - та же, что в примере 12,
- гипотеза 3 из того же списка. Тогда вероятностная модель - та же, что в примере 12,
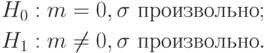
Пример 14. Пусть  - гипотеза 2 из приведенного выше списка, а согласно
- гипотеза 2 из приведенного выше списка, а согласно  результаты наблюдений имеют функцию распределения
результаты наблюдений имеют функцию распределения  , не совпадающую с функцией стандартного нормального распределения
, не совпадающую с функцией стандартного нормального распределения  . Тогда
. Тогда 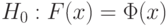 при всех
при всех  (записывается как
(записывается как  );
); 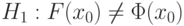 при некотором
при некотором  (т.е. неверно, что
(т.е. неверно, что  ).
).
Примечание. Здесь 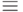 - знак тождественного совпадения функций (т.е. совпадения при всех возможных значениях аргумента
- знак тождественного совпадения функций (т.е. совпадения при всех возможных значениях аргумента  ).
).
Пример 15. Пусть  - гипотеза 3 из приведенного выше списка, а согласно
- гипотеза 3 из приведенного выше списка, а согласно  результаты наблюдений имеют функцию распределения
результаты наблюдений имеют функцию распределения  , не являющуюся нормальной. Тогда
, не являющуюся нормальной. Тогда
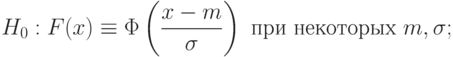
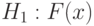 такова, что для любых
такова, что для любых 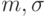 найдется
найдется 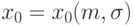 такое, что
такое, что 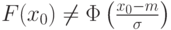 .
.Пример 16. Пусть  - гипотеза 4 из приведенного выше списка, согласно вероятностной модели две выборки извлечены из совокупностей с функциями распределения
- гипотеза 4 из приведенного выше списка, согласно вероятностной модели две выборки извлечены из совокупностей с функциями распределения  и
и 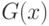 , являющихся нормальными с параметрами
, являющихся нормальными с параметрами 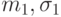 и
и 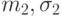 соответственно, а
соответственно, а  - отрицание
- отрицание  . Тогда
. Тогда  , причем
, причем  и
и  произвольны;
произвольны; 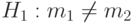 и/или
и/или  .
.
Пример 17. Пусть в условиях примера 16 дополнительно известно, что  . Тогда
. Тогда 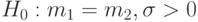 , причем
, причем  и
и  произвольны;
произвольны; 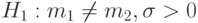 .
.
Пример 18. Пусть  - гипотеза 5 из приведенного выше списка, согласно вероятностной модели две выборки извлечены из совокупностей с функциями распределения
- гипотеза 5 из приведенного выше списка, согласно вероятностной модели две выборки извлечены из совокупностей с функциями распределения  и
и 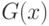 соответственно, а
соответственно, а  - отрицание
- отрицание  . Тогда
. Тогда  , где
, где  - произвольная функция распределения;
- произвольная функция распределения; 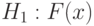 и
и 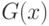 - произвольные функции распределения, причем
- произвольные функции распределения, причем  при некоторых
при некоторых  .
.
Пример 19. Пусть в условиях примера 17 дополнительно предполагается, что функции распределения  и
и 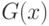 отличаются только сдвигом, т.е.
отличаются только сдвигом, т.е. 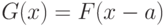 при некотором
при некотором  . Тогда
. Тогда 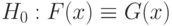 , где
, где  - произвольная функция распределения;
- произвольная функция распределения;  , где
, где  - произвольная функция распределения.
- произвольная функция распределения.
Пример 20. Пусть в условиях примера 14 дополнительно известно, что согласно вероятностной модели ситуации  - функция нормального распределения с единичной дисперсией, т.е. имеет вид
- функция нормального распределения с единичной дисперсией, т.е. имеет вид 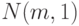 . Тогда
. Тогда 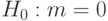 (т.е.
(т.е.  при всех
при всех  ; записывается как
; записывается как 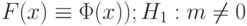 (т.е. неверно, что
(т.е. неверно, что  ).
).
Пример 21. При статистическом регулировании технологических, экономических, управленческих или иных процессов [ [ 2.16 ] ] рассматривают выборку, извлеченную из совокупности с нормальным распределением и известной дисперсией, и гипотезы

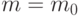 соответствует налаженному ходу процесса, а переход к
соответствует налаженному ходу процесса, а переход к 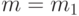 свидетельствует о разладке.
свидетельствует о разладке.Пример 22. При статистическом приемочном контроле [
[
2.16
]
] число дефектных единиц продукции в выборке подчиняется гипергеометрическому распределению, неизвестным параметром является 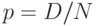 - уровень дефектности, где
- уровень дефектности, где  - объем партии продукции,
- объем партии продукции,  - общее число дефектных единиц продукции в партии. Используемые в нормативно-технической и коммерческой документации (стандартах, договорах на поставку и др.) планы контроля часто нацелены на проверку гипотезы
- общее число дефектных единиц продукции в партии. Используемые в нормативно-технической и коммерческой документации (стандартах, договорах на поставку и др.) планы контроля часто нацелены на проверку гипотезы

 - приемочный уровень дефектности,
- приемочный уровень дефектности, 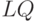 - браковочный уровень дефектности (очевидно, что
- браковочный уровень дефектности (очевидно, что 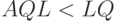 ).
).Пример 23. В качестве показателей стабильности технологического, экономического, управленческого или иного процесса используют ряд характеристик распределений контролируемых показателей, в частности, коэффициент вариации 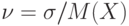 . Требуется проверить нулевую гипотезу
. Требуется проверить нулевую гипотезу

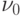 - некоторое заранее заданное граничное значение.
- некоторое заранее заданное граничное значение.Пример 24. Пусть вероятностная модель двух выборок - та же, что в примере 18, математические ожидания результатов наблюдений в первой и второй выборках обозначим 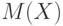 и
и 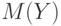 соответственно. В ряде ситуаций проверяют нулевую гипотезу
соответственно. В ряде ситуаций проверяют нулевую гипотезу
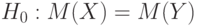
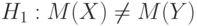
Пример 25. Выше отмечалось большое значение в математической статистике функций распределения, симметричных относительно 0. При проверке симметричности 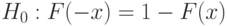 при всех
при всех  , в остальном
, в остальном  произвольна;
произвольна; 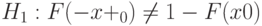 при некотором
при некотором  , в остальном
, в остальном  произвольна.
произвольна.
В вероятностно-статистических методах принятия решений используются и многие другие постановки задач проверки статистических гипотез. Некоторые из них рассматриваются ниже.
Конкретная задача проверки статистической гипотезы полностью описана, если заданы нулевая и альтернативная гипотезы. Выбор метода проверки статистической гипотезы, свойства и характеристики методов определяются как нулевой, так и альтернативной гипотезами. Для проверки одной и той же нулевой гипотезы при различных альтернативных гипотезах следует использовать, вообще говоря, различные методы. Так, в примерах 14 и 20 нулевая гипотеза одна и та же, а альтернативные - различны. Поэтому в условиях примера 14 следует применять методы проверки согласия с фиксированным распределением (например, критерии Колмогорова или омега-квадрат), а в условиях примера 20 - критерий Стьюдента. Если в условиях примера 14 использовать критерий Стьюдента, то он не будет решать поставленных задач (не сможет обнаружить все варианты альтернативных гипотез). Если в условиях примера 20 использовать критерий согласия Колмогорова, то он, напротив, будет решать поставленные задачи, хотя, возможно, и хуже, чем специально приспособленный для этого случая критерий Стьюдента.
При обработке реальных данных большое значение имеет правильный выбор гипотез  и
и  . Принимаемые предположения, например, нормальность распределения, должны быть тщательно обоснованы, в частности, статистическими методами. Отметим, что в подавляющем большинстве конкретных прикладных постановок распределение результатов наблюдений отлично от нормального [
[
2.16
]
].
. Принимаемые предположения, например, нормальность распределения, должны быть тщательно обоснованы, в частности, статистическими методами. Отметим, что в подавляющем большинстве конкретных прикладных постановок распределение результатов наблюдений отлично от нормального [
[
2.16
]
].
Часто возникает ситуация, когда вид нулевой гипотезы вытекает из постановки прикладной задачи, а вид альтернативной гипотезы не ясен. В таких случаях следует рассматривать альтернативную гипотезу наиболее общего вида и использовать методы, решающие поставленную задачу при всех возможных  . В частности при проверке гипотезы 2 (из приведенного выше списка) как нулевой следует в качестве альтернативной гипотезы использовать
. В частности при проверке гипотезы 2 (из приведенного выше списка) как нулевой следует в качестве альтернативной гипотезы использовать  из примера 14, а не из примера 20, если нет специальных обоснований нормальности распределения результатов наблюдений при альтернативной гипотезе.
из примера 14, а не из примера 20, если нет специальных обоснований нормальности распределения результатов наблюдений при альтернативной гипотезе.
Статистические гипотезы бывают параметрические и непараметрические. Предположение, которое касается неизвестного значения параметра распределения, входящего в некоторое параметрическое семейство распределений, называется параметрической гипотезой (напомним, что параметр может быть и многомерным). Предположение, при котором вид распределения неизвестен (т.е. не предполагается, что оно входит в некоторое параметрическое семейство распределений), называется непараметрической гипотезой. Таким образом, если распределение  результатов наблюдений в выборке согласно принятой вероятностной модели входит в некоторое параметрическое семейство
результатов наблюдений в выборке согласно принятой вероятностной модели входит в некоторое параметрическое семейство 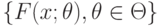 , т.е.
, т.е. 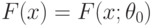 при некотором
при некотором 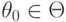 , то рассматриваемая гипотеза - параметрическая, в противном случае - непараметрическая.
, то рассматриваемая гипотеза - параметрическая, в противном случае - непараметрическая.
Если и  и
и  - параметрические гипотезы, то задача проверки статистической гипотезы - параметрическая. Если хотя бы одна из гипотез
- параметрические гипотезы, то задача проверки статистической гипотезы - параметрическая. Если хотя бы одна из гипотез  и
и  - непараметрическая, то задача проверки статистической гипотезы - непараметрическая. Другими словами, если вероятностная модель ситуации - параметрическая, т.е. полностью описывается в терминах того или иного параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы - параметрическая. Если же вероятностная модель ситуации - непараметрическая, т.е. ее нельзя полностью описать в терминах какого-либо параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы - непараметрическая. В примерах 11-13, 16, 17, 20-22 даны постановки параметрических задач проверки гипотез, а в примерах 14, 15, 18, 19, 23-25 - непараметрических.
Непараметрические задачи делятся на два класса: в одном из них речь идет о проверке утверждений, касающихся функций распределения (примеры 14, 15, 18, 19, 25), во втором - о проверке утверждений, касающихся характеристик распределений (примеры 23, 24).
- непараметрическая, то задача проверки статистической гипотезы - непараметрическая. Другими словами, если вероятностная модель ситуации - параметрическая, т.е. полностью описывается в терминах того или иного параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы - параметрическая. Если же вероятностная модель ситуации - непараметрическая, т.е. ее нельзя полностью описать в терминах какого-либо параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы - непараметрическая. В примерах 11-13, 16, 17, 20-22 даны постановки параметрических задач проверки гипотез, а в примерах 14, 15, 18, 19, 23-25 - непараметрических.
Непараметрические задачи делятся на два класса: в одном из них речь идет о проверке утверждений, касающихся функций распределения (примеры 14, 15, 18, 19, 25), во втором - о проверке утверждений, касающихся характеристик распределений (примеры 23, 24).
Статистическая гипотеза называется простой, если она однозначно задает распределение результатов наблюдений, вошедших в выборку. В противном случае статистическая гипотеза называется сложной. Гипотеза 2 из приведенного выше списка, нулевые гипотезы в примерах 11, 12, 14, 20, нулевая и альтернативная гипотезы в примере 21 - простые, все остальные упомянутые выше гипотезы - сложные.
Однозначно определенный способ проверки статистических гипотез называется статистическим критерием. Статистический критерий строится с помощью статистики 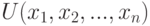 - функции от результатов наблюдений
- функции от результатов наблюдений 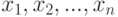 . В пространстве значений статистики
. В пространстве значений статистики  выделяют критическую область
выделяют критическую область  , т.е. область со следующим свойством: если значения применяемой статистики принадлежат данной области, то отклоняют (иногда говорят - отвергают) нулевую гипотезу, в противном случае - не отвергают (т.е. принимают).
, т.е. область со следующим свойством: если значения применяемой статистики принадлежат данной области, то отклоняют (иногда говорят - отвергают) нулевую гипотезу, в противном случае - не отвергают (т.е. принимают).
Статистику  , используемую при построении определенного статистического критерия, называют статистикой этого критерия. Например, в задаче проверки статистической гипотезы, приведенной в примере 14, применяют критерий Колмогорова, основанный на статистике
, используемую при построении определенного статистического критерия, называют статистикой этого критерия. Например, в задаче проверки статистической гипотезы, приведенной в примере 14, применяют критерий Колмогорова, основанный на статистике
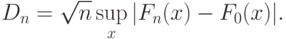
При этом 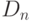 называют статистикой критерия Колмогорова.
называют статистикой критерия Колмогорова.
Частным случаем статистики  является векторзначная функция результатов наблюдений
является векторзначная функция результатов наблюдений 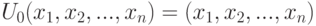 , значения которой - набор результатов наблюдений. Если
, значения которой - набор результатов наблюдений. Если  - числа, то
- числа, то 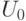 - набор
- набор  чисел, т.е. точка
чисел, т.е. точка  -мерного пространства. Ясно, что статистика критерия
-мерного пространства. Ясно, что статистика критерия  является функцией от
является функцией от 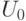 , т.е.
, т.е. 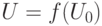 . Поэтому можно считать, что
. Поэтому можно считать, что  - область в том же
- область в том же  -мерном пространстве, нулевая гипотеза отвергается, если
-мерном пространстве, нулевая гипотеза отвергается, если 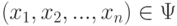 , и принимается в противном случае.
, и принимается в противном случае.
В вероятностно-статистических методах принятия решений, статистические критерии, как правило, основаны на статистиках  , принимающих числовые значения, и критические области имеют вид
, принимающих числовые значения, и критические области имеют вид
 |
( 9) |
 - некоторые числа.
- некоторые числа.Статистические критерии делятся на параметрические и непараметрические. Параметрические критерии используются в параметрических задачах проверки статистических гипотез, а непараметрические - в непараметрических задачах.
При проверке статистической гипотезы возможны ошибки. Есть два рода ошибок. Ошибка первого рода заключается в том, что отвергают нулевую гипотезу, в то время как в действительности эта гипотеза верна. Ошибка второго рода состоит в том, что принимают нулевую гипотезу, в то время как в действительности эта гипотеза неверна.
Вероятность ошибки первого рода называется уровнем значимости и обозначается  . Таким образом,
. Таким образом, 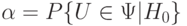 , т.е. уровень значимости
, т.е. уровень значимости  - это вероятность события
- это вероятность события  , вычисленная в предположении, что верна нулевая гипотеза
, вычисленная в предположении, что верна нулевая гипотеза  .
.
Уровень значимости однозначно определен, если  - простая гипотеза. Если же
- простая гипотеза. Если же  - сложная гипотеза, то уровень значимости, вообще говоря, зависит от функции распределения результатов наблюдений, удовлетворяющей
- сложная гипотеза, то уровень значимости, вообще говоря, зависит от функции распределения результатов наблюдений, удовлетворяющей  . Статистику критерия
. Статистику критерия  обычно строят так, чтобы вероятность события
обычно строят так, чтобы вероятность события  не зависела от того, какое именно распределение (из удовлетворяющих нулевой гипотезе
не зависела от того, какое именно распределение (из удовлетворяющих нулевой гипотезе  ) имеют результаты наблюдений. Для статистик критерия
) имеют результаты наблюдений. Для статистик критерия  общего вида под уровнем значимости понимают максимально возможную ошибку первого рода. Максимум (точнее, супремум) берется по всем возможным распределениям, удовлетворяющим нулевой гипотезе
общего вида под уровнем значимости понимают максимально возможную ошибку первого рода. Максимум (точнее, супремум) берется по всем возможным распределениям, удовлетворяющим нулевой гипотезе  , т.е.
, т.е. 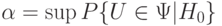 .
.
Если критическая область имеет вид, указанный в формуле (9), то
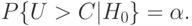
Если  задано, то из последнего соотношения определяют
задано, то из последнего соотношения определяют  . Часто поступают по иному - задавая
. Часто поступают по иному - задавая  (обычно
(обычно 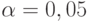 , иногда
, иногда 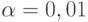 или
или 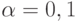 , другие значения
, другие значения  используются гораздо реже), определяют
используются гораздо реже), определяют  из уравнения (10), обозначая его
из уравнения (10), обозначая его 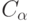 , и используют критическую область
, и используют критическую область 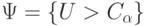 с заданным уровнем значимости
с заданным уровнем значимости  .
.
Вероятность ошибки второго рода есть 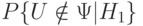 . Обычно используют не эту вероятность, а ее дополнение до 1, т.е.
. Обычно используют не эту вероятность, а ее дополнение до 1, т.е. 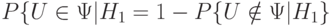 . Эта величина носит название мощности критерия. Итак, мощность критерия - это вероятность того, что нулевая гипотеза будет отвергнута, когда альтернативная гипотеза верна.
. Эта величина носит название мощности критерия. Итак, мощность критерия - это вероятность того, что нулевая гипотеза будет отвергнута, когда альтернативная гипотеза верна.
Понятия уровня значимости и мощности критерия объединяются в понятии функции мощности критерия - функции, определяющей вероятность того, что нулевая гипотеза будет отвергнута. Функция мощности зависит от критической области  и действительного распределения результатов наблюдений. В параметрической задаче проверки гипотез распределение результатов наблюдений задается параметром
и действительного распределения результатов наблюдений. В параметрической задаче проверки гипотез распределение результатов наблюдений задается параметром  . В этом случае функция мощности обозначается
. В этом случае функция мощности обозначается 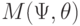 и зависит от критической области
и зависит от критической области  и действительного значения исследуемого параметра
и действительного значения исследуемого параметра  . Если
. Если
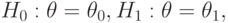
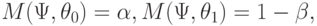
 - вероятность ошибки первого рода,
- вероятность ошибки первого рода,  - вероятность ошибки второго рода. В статистическом приемочном контроле
- вероятность ошибки второго рода. В статистическом приемочном контроле  - риск изготовителя,
- риск изготовителя,  - риск потребителя. При статистическом регулировании технологического процесса
- риск потребителя. При статистическом регулировании технологического процесса  - риск излишней наладки,
- риск излишней наладки,  - риск незамеченной разладки.
- риск незамеченной разладки.Функция мощности 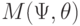 в случае одномерного параметра
в случае одномерного параметра  обычно достигает минимума, равного
обычно достигает минимума, равного  , при
, при  , монотонно возрастает при удалении от
, монотонно возрастает при удалении от 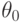 и приближается к 1 при
и приближается к 1 при 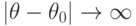 .
.
В ряде вероятностно-статистических методов принятия решений используется оперативная характеристика 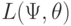 - вероятность принятия нулевой гипотезы в зависимости от критической области
- вероятность принятия нулевой гипотезы в зависимости от критической области  и действительного значения исследуемого параметра
и действительного значения исследуемого параметра  . Ясно, что
. Ясно, что
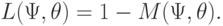
Основной характеристикой статистического критерия является функция мощности. Для многих задач проверки статистических гипотез разработан не один статистический критерий, а целый ряд. Чтобы выбрать из них определенный критерий для использования в конкретной практической ситуации, проводят сравнение критериев по различным показателям качества [ [ 2.16 ] , прил. 3], прежде всего с помощью их функций мощности. В качестве примера рассмотрим лишь два показателя качества критерия проверки статистической гипотезы - состоятельность и несмещенность.
Пусть объем выборки  растет, а
растет, а 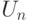 и
и 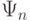 - статистики критерия и критические области соответственно. Критерий называется состоятельным, если
- статистики критерия и критические области соответственно. Критерий называется состоятельным, если

Статистический критерий называется несмещенным, если для любого 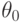 , удовлетворяющего
, удовлетворяющего  , и любого
, и любого 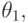 удовлетворяющего
удовлетворяющего  , справедливо неравенство
, справедливо неравенство
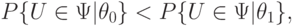
 вероятность отвергнуть
вероятность отвергнуть  меньше, чем при справедливости
меньше, чем при справедливости  .
.При наличии нескольких статистических критериев в одной и той же задаче проверки статистических гипотез следует использовать состоятельные и несмещенные критерии.
