|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Компьютеры в прикладной статистике
Методы статистических испытаний (Монте-Карло). Многие информационные технологии в области прикладной статистики опираются на использование методов статистических испытаний. Этот термин применяется для обозначения компьютерных технологий, в которых в модель реального явления или процесса искусственно вводится большое число случайных элементов. Обычно моделируется последовательность независимых одинаково распределенных случайных величин или же последовательность, построенная на ее основе, например, последовательность накапливающихся (кумулятивных) сумм.
Необходимость в методе статистических испытаний возникает потому, что чисто теоретические методы дают точное решение, как правило, лишь в исключительных случаях. Либо тогда, когда исходные случайные величины имеют вполне определенные функции распределения, например, нормальные, чего, как правило, не бывает. Либо когда объемы выборок очень велики (с практической точки зрения - бесконечны).
Не только в задачах обработки данных возникает необходимость в методе статистических испытаний. Она не менее актуальна и при экономико-математическом моделировании технических, социально-экономических, медицинских и иных процессов. Представим себе всем знакомый объект - торговый зал самообслуживания по продаже продовольственных товаров. Сколько нужно работников в зале, сколько касс? Необходимо просчитать загрузку в разное время суток, в разные сезоны года, с учетом замены товаров и смены сотрудников. Нетрудно увидеть, что теоретическому анализу подобная система не поддается, а компьютерному - вполне.
Методы статистических испытаний стали развиваться после Второй мировой войны с появлением компьютеров. Второе название - методы Монте-Карло - они получили по наиболее известному игорному дому, а точнее, по его рулетке, поскольку исходный материал для получения случайных чисел с произвольным распределением - это случайные натуральные числа.
В методах статистических испытаний можно выделить две составляющие. Базой являются датчики псевдослучайных чисел. Результатом работы таких датчиков являются последовательности чисел, которые обладают некоторыми свойствами последовательностей случайных величин (в смысле теории вероятностей). Надстройкой являются различные алгоритмы, использующие последовательности псевдослучайных чисел.
Что же это могут быть за алгоритмы? Приведем примеры. Пусть мы изучаем распределение некоторой статистики при заданном объеме выборки. Тогда естественно много раз (например, 100000 раз) смоделировать выборку заданного объема (т.е. набор независимых одинаково распределенных случайных величин) и рассчитать значение статистики. Затем по 100000 значениям статистики можно достаточно точно построить функцию распределения изучаемой статистики, оценить ее характеристики. Однако эта схема годится лишь для так называемой "свободной от распределения" статистики, распределение которой не зависит от распределения элементов выборки. Если же такая зависимость есть, то одной точкой моделирования не обойдешься, придется много раз моделировать выборку, беря различные распределения, меняя параметры. Чтобы общее время моделирования было приемлемым, возможно, придется сократить число моделирований в одной точке, зато увеличив общее число точек. Точность моделирования может быть оценена по общим правилам выборочных обследований.
Второй пример - частично описанное выше моделирование работы торгового зала самообслуживания по продаже продовольственных товаров. Здесь одна последовательность псевдослучайных чисел описывает интервалы между появлениями покупателей, вторая, третья и т.д. связаны с выбором ими первого, второго и т.д. товаров в зале (например, число - номер в перечне товаров). Короче, все действия покупателей, продавцов, работников предприятия разбиты на операции, каждая операция, в продолжительности или иной характеристике которой имеется случайность, моделируется с помощью соответствующей последовательности псевдослучайных чисел. Затем итоги работы сотрудников торговой организации и зала в целом выражаются через характеристики случайных величин. Формулируется критерий оптимальности, решается задача оптимизации и находятся оптимальные значения параметров. В частности, оптимальные планы статистического контроля строятся на основе вероятностно-статистических моделей [ [ 2.15 ] ].
Датчики псевдослучайных чисел. Теперь обсудим свойства датчиков псевдослучайных чисел. Здесь употребляется термин "псевдослучайные", а не "случайные". Это весьма важно. Дело в том, что за последние 50 лет обсуждались в основном три принципиально разных варианта получения последовательностей чисел, которые в дальнейшем использовались в методах статистических испытаний.
Первый - таблица случайных чисел. К сожалению, объем любой таблицы конечен, и сколько-нибудь сложные расчеты с ее помощью невозможны. Через некоторое время приходится повторяться. Кроме того, обычно обнаруживались те или иные отклонения от случайности.
Второй - физические датчики случайных чисел. Основной недостаток - нестабильность, непредсказуемые отклонения от заданного распределения (обычно - равномерного).
Третий - расчетный. В простейшем случае каждый следующий член последовательности рассчитывается по предыдущему. Например, так:

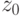 - начальное значение (заданное целое положительное число),
- начальное значение (заданное целое положительное число),  - параметр алгоритма (заданное целое положительное число),
- параметр алгоритма (заданное целое положительное число), 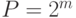 , где
, где  - число двоичных разрядов представления чисел, с которыми манипулирует компьютер. Знак
- число двоичных разрядов представления чисел, с которыми манипулирует компьютер. Знак 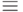 здесь означает теоретико-числовую операцию сравнения, т.е. взятие дробной части от
здесь означает теоретико-числовую операцию сравнения, т.е. взятие дробной части от 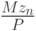 и отбрасывание целой части.
и отбрасывание целой части.В настоящее время применяется именно третий вариант. Совершенно ясно, что он не соответствует интуитивному представлению о случайности. Например, очевидно, что по предыдущему элементу случайной последовательности с независимыми элементами нельзя предсказать значение следующего элемента. А приведенная выше формула как раз и дает способ такого предсказания. Расчетный путь получения последовательности псевдослучайных чисел противоречит не только интуиции, но и подходу к определению случайности на основе теории алгоритмов, развитому акад. А.Н. Колмогоровым и его учениками в 1960-х годах. Однако во многих прикладных задачах он работает, и это основное.
Методу статистических испытаний посвящена обширная литература (см., например, [ [ 13.10 ] , [ 13.11 ] , [ 13.15 ] ]). Время от времени обнаруживаются недостатки у популярных датчиков псевдослучайных чисел. Так, например, в середине 1980-х годов выяснилось, что для одного из наиболее известных датчиков три последовательных значения связаны линейной зависимостью
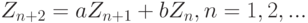
После этого в 1985 г. в журнале "Заводская лаборатория" началась дискуссия о качестве датчиков псевдослучайных чисел, которая продолжалась до 1993 г. и закончилась статьей проф. С.М.Ермакова [ [ 13.12 ] ] и нашим комментарием.
Можно подвести следующие итоги дискуссии. Во многих случаях решаемая методом статистических испытаний задача сводится к оценке вероятности попадания в некоторую область в многомерном пространстве фиксированной размерности. Тогда из чисто математических соображений теории чисел следует, что с помощью датчиков псевдослучайных чисел поставленная задача решается корректно. Сводка соответствующих математических обоснований приведена, например, в работе С.М. Ермакова [ [ 13.12 ] ].
В других случаях приходится рассматривать вероятности попадания в области в пространствах переменной размерности. Типичным примером является ситуация, когда на каждом шагу проводится проверка, и по ее результатам либо остаемся в данном пространстве, либо переходим в пространство большей размерности. Например, в "Многомерный статистический анализ" при оценивании степени многочлена либо останавливались на данной степени, либо увеличивали степень, переходя в параметрическое пространство большей размерности. Так вот, вопрос об обоснованности применения метода статистических испытаний (а точнее, о свойствах датчиков псевдослучайных чисел) в случае пространств переменной размерности остается в настоящее время открытым. О важности этой проблемы говорил академик РАН Ю.В. Прохоров на Первом Всемирном Конгрессе Общества математической статистики и теории вероятностей им. Бернулли (Ташкент, 1986 г.).
Имитационное моделирование. Поскольку мы постоянно говорим о моделировании, приведем несколько общих формулировок.
Модель в общем смысле (обобщенная модель) - это создаваемый с целью получения и (или) хранения информации специфический объект (в форме мысленного образа, описания знаковыми средствами либо материальной системы), отражающей свойства, характеристики и связи объекта-оригинала произвольной природы, существенные для задачи, решаемой субъектом (это определение взято из монографии [ [ 13.24 ] , с.44]).
Например, в менеджменте производственных систем используют:
- модели технологических процессов (контроль и управление по технико-экономическим критериям, АСУ ТП - автоматизированные системы управления технологическими процессами);
- модели управления качеством продукции (в частности, модели оценки и контроля надежности);
- модели массового обслуживания (теории очередей);
- модели управления запасами (в современной терминологии - модели логистики, т.е. теории и практики управления материальными, финансовыми и информационными потоками);
- имитационные и эконометрические модели деятельности предприятия (как единого целого) и управления им (АСУ предприятием) и др.
Согласно академику РАН Н.Н. Моисееву [22, с.213], имитационная система - это совокупность моделей, имитирующих протекание изучаемого процесса, объединенная со специальной системой вспомогательных программ и информационной базой, позволяющих достаточно просто и оперативно реализовать вариантные расчеты. Другими словами, имитационная система - это совокупность имитационных моделей. А имитационная модель предназначена для ответов на вопросы типа: "Что будет, если…" Что будет, если параметры примут те или иные значения? Что будет с ценой на продукцию, если спрос будет падать, а число конкурентов расти? Что будет, если государство резко усилит вмешательство в экономику? Что будет, если остановку общественного транспорта перенесут на 100 м дальше от входа в торговый зал, о котором шла речь выше, и поток покупателей резко упадет? Кроме компьютерных моделей, на вопросы подобного типа часто отвечают эксперты при использовании метода сценариев [ [ 2.15 ] , [ 13.39 ] ].
При имитационном моделировании часто используется метод статистических испытаний (Монте-Карло). Теорию и практику машинных имитационных экспериментов с моделями экономических систем еще 30 лет назад подробно разобрал Т. Нейлор в классической монографии [ [ 13.23 ] ]. Вернемся к внутристатистическому применению датчиков псевдослучайных чисел.
