НОУ ИНТУИТ | Прикладная статистика. Лекция 4: Теоретическая база прикладной статистики

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2009 | Доступ: свободный | Студентов: 4084 / 1035 | Оценка: 4.66 / 4.45 | Длительность: 54:13:00

Темы: Математика, Экономика

Специальности: Экономист

|

Вам нравится? Нравится 61 студенту

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В лекции собраны основные математико-статистические утверждения, постоянно используемые при математическом обосновании методов прикладной статистики: законы больших чисел, центральные предельные теоремы, теоремы о наследовании сходимости. Уделено внимание методу линеаризации и принципу инвариантности, а также вопросу устойчивости выводов.

Ключевые слова: ПО, линеаризация, вероятность, статистика, неравенство, элементарное события, закон больших чисел, конечные, выборочной средней, медиана, предел, функция, работ, значение, сходимость, вектор, матрица, нормальное распределение, математическим ожиданием, определитель матрицы, пространство, подмножество, метрика, множества, окрестность, расстояние, отношение, запись, наследование, метрическое пространство, разбиение, пересечение, объединение, линейное пространство, норма, длина, коэффициенты, линейная функция, случайная величина, дисперсия, эмпирическая функция, функциональное пространство, интеграл, функция принадлежности, теоретико-множественные операции, пересечение множеств, связь, нечеткое множество, определение, ссылка, доказательство, операции, Законы де Моргана, операция пересечения, постоянное значение, равенство, Произведение, алгебра, мера, делимое, математическая индукция, Построение математической модели, точность, адекватность модели, устойчивость, решение дифференциального уравнения, корректность, регуляризация, математическое программирование, объект, отображение, диаметр, интегрирование, иерархия, непрерывная модель, класс, асимптотическая устойчивость, метод статистических испытаний, нормальный закон, анализ, биномиальные коэффициенты, факториал, выражение, степенные ряды, разложение в ряд, длина цепочки, преобразования формул, нижняя граница, реальная таблица, задача оценки, константы, распределение Коши, улучшение, размерность, инструментарий, статистический критерий, объем выборки, компьютер, погрешность, квантование, Относительной погрешностью, затраты, нечеткая переменная, кластерный анализ

В настоящей лекции собраны основные математико-статистические утверждения, постоянно используемые при математическом обосновании методов прикладной статистики. Эти утверждения отнюдь не всегда легко найти в литературе по теории вероятностей и математической статистике. Например, такие рассматриваемые далее теоремы и методы, как многомерная центральная предельная теорема, теоремы о наследовании сходимости и метод линеаризации, даже не включены в энциклопедию "Вероятность и математическая статистика" [ [ 4.4 ] ] - наиболее полный свод знаний по этой тематике. Последний факт наглядно демонстрирует разрыв между математической дисциплиной "теория вероятностей и математическая статистика" и потребностями прикладной статистики.

4.1. Законы больших чисел

Законы больших чисел позволяют описать поведение сумм случайных величин. Примером является следующий результат, обобщающий полученный ранее в $\S$ 2.2. Там было доказано следующее утверждение.

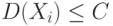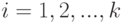Теорема Чебышева. Пусть случайные величины X_1, X_2,..., X_k попарно независимы и существует число такое, что $D(X_i)\le C$ при всех i = 1, 2, ..., k . Тогда для любого положительного $\varepsilon$ выполнено неравенство

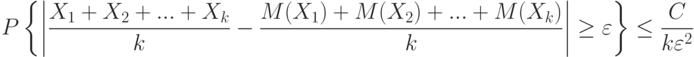$P \left\{ \left| \frac{X_1+X_2+...+X_k}{k}-\frac{M(X_1)+M(X_2)+...+M(X_k)}{k} \right|\ge\varepsilon \right\} \le\frac{C}{k\varepsilon^2}$

( 1)

Частным случаем теоремы Чебышева является теорема Бернулли - первый в истории вариант закона больших чисел.

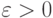Теорема Бернулли. Пусть - число наступлений события в независимых (попарно) испытаниях, и есть вероятность наступления события в каждом из испытаний. Тогда при любом $\varepsilon>0$ справедливо неравенство

$P \left\{ \left| \frac{m}{k}-p \right|\ge\varepsilon \right\} \le\frac{p(1-p)}{k\varepsilon^2}.$

( 2)

Ясно, что при росте выражения в правых частях формул (1) и (2) стремятся к 0. Таким образом, среднее арифметическое попарно независимых случайных величин сближается со средним арифметическим их математических ожиданий.

Напомним, что в "Основы вероятностно-статистических методов описания неопределенностей" шла речь лишь о пространствах элементарных событий из конечного числа элементов. Однако приведенные теоремы верны и в общем случае - для произвольных пространств элементарных событий. Однако в условие закона больших чисел необходимо добавить требование существования дисперсий. Легко видеть, что если существуют дисперсии, то существуют и математические ожидания. Закон больших чисел в форме Чебышева приобретает следующий вид.

Теорема Чебышева [ [ 2.3 ] , с.147]. Если X_1,X_2,...,X_k,.. . - последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной,

$D(X_1)\le C,D(X_2)\le C,...,D(X_i)\le C,...$

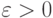то, каково бы ни было постоянное $\varepsilon>0$ ,

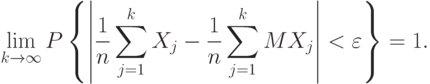$\lim_{k\rightarrow\infty}P \left\{ \left| \frac{1}{n}\sum_{j=1}^k X_j-\frac{1}{n}\sum_{j=1}^k MX_j \right|<\varepsilon \right\}=1.$

( 3)

С точки зрения прикладной статистики ограниченность дисперсий вполне естественна. Она вытекает, например, из ограниченности диапазона изменения практически всех величин, используемых при реальных расчетах.

В 1923 г. А.Я. Хинчин показал, что если случайные величины не только независимы, но и одинаково распределены, то существование у них математического ожидания является необходимым и достаточным условием для применимости закона больших чисел [ [ 2.3 ] , с.150].

Теорема [ [ 2.3 ] , с.150-151]. Для того чтобы для последовательности X_1,X_2,...,X_k,.. . (как угодно зависимых) случайных величин при любом положительном $\varepsilon$ выполнялось соотношение (3), необходимо и достаточно, чтобы при $n\rightarrow\infty$

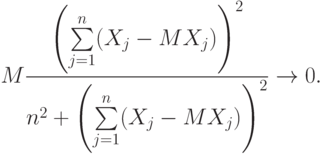
$M\frac{\left(\sum\limits_{j=1}^n(X_j-MX_j)\right)^2}{n^2+\left(\sum\limits_{j=1}^n(X_j-MX_j)\right)^2}\rightarrow 0.$

Законы больших чисел для случайных величин служат основой для аналогичных утверждений для случайных элементов в пространствах более сложной природы, в частности, в пространствах произвольной природы (см. п.5.5 далее). Однако здесь мы ограничимся классическими формулировками, служащими основой для современной прикладной статистики.

Смысл классических законов больших чисел состоит в том, что выборочное среднее арифметическое независимых одинаково распределенных случайных величин приближается (сходится) к математическому ожиданию этих величин. Другими словами, выборочные средние сходятся к теоретическому среднему.

Это утверждение справедливо и для других видов средних. Например, выборочная медиана сходится к теоретической медиане. Это утверждение - тоже закон больших чисел, но не классический.

Существенным продвижением в теории вероятностей во второй половине ХХ в. явилось введение средних величин в пространствах произвольной природы и получение для них законов больших чисел, т.е. утверждений, состоящих в том, что эмпирические (т.е. выборочные) средние сходятся к теоретическим средним. Эти результаты будут рассмотрены в п.5.5 ниже.

Дальше >>

Авторизоваться

Прикладная статистика

Теоретическая база прикладной статистики

4.1. Законы больших чисел

Вопросы и ответы