Теоретическая база прикладной статистики

4.7. Устойчивость выводов и принцип уравнивания погрешностей

Устойчивость математических моделей. Проблемам познания, в том числе в технических исследованиях, естественно-научных и социально-экономических областях, посвящено огромное количество работ. Однако это не значит, что обо всем в этой области уже все сказано. А о некоторых положениях целесообразно говорить еще и еще раз, пока они ни станут общеизвестными.

В идеале каждую модель порождения и анализа данных следовало бы рассматривать как аксиоматическую теорию. В этом идеальном случае создание и использование модели происходит в соответствии с известной триадой "практика - теория - практика". А именно, сначала вводятся некоторые математические объекты, соответствующие интересующим исследователя реальным объектам, и на основе представлений о свойствах реальных объектов формулируются необходимые для успешного моделирования свойства математических объектов, которые и принимаются в качестве аксиом. Затем аксиоматическая теория развивается как часть математики, вне связи с представлениями о реальных объектах. На заключительном этапе полученные в математической теории результаты интерпретируются содержательно. Получаются утверждения о реальных объектах, являющиеся следствиями тех и только тех их свойств, которые ранее были аксиоматизированы.

После построения математической модели реального явления или процесса встает вопрос об ее адекватности. Иногда ответ на этот вопрос может дать эксперимент. Рассогласование модельных и экспериментальных данных следует интерпретировать как признак неадекватности некоторых из принятых аксиом. Однако для проверки адекватности социально-экономических моделей зачастую невозможно поставить решающий эксперимент в отличие, скажем, от физических моделей. С другой стороны, для одного и того же явления или процесса, как правило, можно составить много возможных моделей, если угодно, много разновидностей одной базовой модели. Поэтому необходимы какие-то дополнительные условия, которые позволяли бы из множества возможных моделей и эконометрических методов анализа данных выбрать наиболее подходящие. В качестве одного из подобных условий выдвигается требование устойчивости модели и метода анализа данных относительно допустимых отклонений исходных данных и предпосылок модели или условий применимости метода.

Отметим, что в большинстве случаев исследователей и практических работников интересуют не столько сами модели и методы, сколько решения, которые с их помощью принимаются. Ведь модели и методы для того и разрабатываются, чтобы подготавливать решения. Вместе с тем очевидно, что решения, как правило, принимаются в условиях неполноты информации. Так, любые числовые параметры известны лишь с некоторой точностью. Введение в рассмотрение возможных неопределенностей исходных данных требует каких-то заключений относительно устойчивости принимаемых решений по отношению к этим допустимым неопределенностям.

Введем основные понятия согласно монографии [ [ 1.15 ] ]. Будем считать, что имеются исходные данные, на основе которых принимаются решения. Способ переработки (отображения) исходных данных в решение назовем моделью. Таким образом, с общей точки зрения модель - это функция, переводящая исходные данные в решение, т.е. способ перехода значения не имеет. Очевидно, любая рекомендуемая для практического использования модель должна быть исследована на устойчивость относительно допустимых отклонений исходных данных. Укажем некоторые возможные применения результатов подобного исследования:

• заказчик научно-исследовательской работы получает представление о точности предлагаемого решения;
• удается выбрать из многих моделей наиболее адекватную;
• по известной точности определения отдельных параметров модели удается указать необходимую точность нахождения остальных параметров;
• переход к случаю "общего положения" позволяет получать более сильные с математической точки зрения результаты.

Примеры. По каждому из четырех перечисленных возможных применений в [ [ 1.15 ] , [ 2.15 ] ] приведены различные примеры. В прикладной статистике точность предлагаемого решения связана с разбросом исходных данных и с объемом выборки. Выбору наиболее адекватной модели посвящены темы, рассмотренные в лекциях "Статистический анализ числовых величин" и "Статистический анализ числовых величин" , связанные с обсуждением моделей однородности и регрессии. Использование рационального объема выборки в статистике интервальных данных ( "Статистический анализ числовых величин" ) исходит из принципа уравнивания погрешностей. Этот принцип основан на том, что по известной точности определения отдельных параметров модели удается указать необходимую точность нахождения остальных параметров. Другим примером применения принципа уравнивания погрешностей является нахождение необходимой точности оценивания параметров в моделях логистики, рассмотренных в главе 5 монографии [ [ 1.15 ] ]. Наконец, переходом к случаю "общего положения" в прикладной статистике является, в частности, переход к непараметрическим методам, необходимый из-за невозможности обосновать принадлежность результатов наблюдений к тем или иным параметрическим семействам.

Специалисты по математическому моделированию и теории управления считают устойчивость одной из важных характеристик технических, социально-экономических, медицинских и иных моделей. Достаточно глубокие исследования ведутся по ряду направлений.

Первоначальное изучение влияния малого изменения одного параметра обычно называют анализом чувствительности. Оно описывается значением частной производной. Если модель задается дифференцируемой функцией, то итог анализа чувствительности - вектор значений частных производных в анализируемой точке.

Теория устойчивости решений дифференциальных уравнений развивается по крайней мере с XIX в. [ [ 4.21 ] ]. Выработаны соответствующие понятия - устойчивость по Ляпунову, корректность, доказаны глубокие теоремы. Для решения некорректных задач академиком АН СССР А.Н. Тихоновым в начале 1960-х годов был предложен метод регуляризации. Модели явлений и процессов, выражаемые с помощью дифференциальных уравнений, могут быть исследованы на устойчивость путем применения хорошо разработанного математического аппарата.

Вопросы устойчивости изучались практически во всех направлениях прикладных математических методов - и в математическом программировании, и в теории массового обслуживания (теории очередей), и в эколого-экономических моделях, и в различных областях эконометрики.

Общая схема устойчивости. Прежде чем переходить к конкретным постановкам, обсудим "общую схему устойчивости", дающую понятийную базу для обсуждения проблем устойчивости в различных предметных областях.

Определение 1. Общей схемой устойчивости называется объект .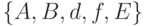

Здесь - множество, интерпретируемое как пространство исходных данных; - множество, называемое пространством решений. Однозначное отображение 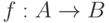называется моделью. Об этих трех составляющих общей схемы устойчивости уже шла речь выше.

Оставшиеся два понятия нужны для уточнения понятий близости в пространстве исходных данных и пространстве решений. Подобные уточнения могут быть сделаны разными способами. Самое "слабое" уточнение - на языке топологических пространств. Тогда возможны качественные выводы (сходится - не сходится), но не количественные расчеты. Самое "сильное" уточнение - на языке метрических пространств. Промежуточный вариант - используются показатели различия (отличаются от метрик тем, что не обязательно выполняются неравенства треугольника) или вводимые ниже понятия.

Пусть - показатель устойчивости, т.е. неотрицательная функция, определенная на подмножествах множества и такая, что из 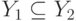вытекает . Часто показатель устойчивости 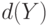определяется с помощью метрики, псевдометрики или показателя различия (меры близости) как диаметр множества , т.е.

Таким образом, говоря попросту, в пространстве решений с помощью показателя устойчивости вокруг образа исходных данных может быть сформирована система окрестностей. Но сначала надо такую систему сформировать в пространстве исходных данных.

Пусть 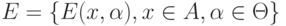- совокупность допустимых отклонений. То есть система подмножеств множества такая, что каждому элементу множества исходных данных 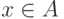и каждому значению параметра из некоторого множества параметров соответствует подмножество 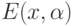множества исходных данных. Оно называется множеством допустимых отклонений в точке при значении параметра, равном . Наглядно можно представить себе, что вокруг точки взята окрестность радиуса .

Определение 2. Показателем устойчивости в точке при значении параметра, равном , называется число

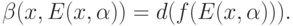
Другими словами, это - диаметр образа множества допустимых колебаний при рассматриваемом в качестве модели отображении. Очевидно, что этот показатель устойчивости зависит как от исходных данных, так и от диаметра множества возможных отклонений в исходном пространстве. Для непрерывных функций показатель устойчивости обычно называется модулем непрерывности.

Естественно посмотреть, насколько сузится образ окрестности возможных отклонений при максимально возможном сужении этой окрестности.

Определение 3. Абсолютным показателем устойчивости в точке называется число

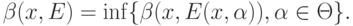
Если функция непрерывна, а окрестности - именно те, о которых идет речь в математическом анализе, то максимальное сужение означает сужение к точке и абсолютный показатель устойчивости равен 0. Но в теории измерений и статистике интервальных данных мы сталкиваемся с совсем иными ситуациями. В теории измерений окрестностью исходных данных являются все те вектора, что получаются из исходного путем преобразования координат с помощью допустимого преобразования шкалы, а допустимое преобразование шкалы берется из соответствующей группы допустимых преобразований. В статистике интервальных данных под окрестностью исходных данных естественно понимать - при описании выборки - куб с ребрами 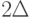и центром в исходном векторе. И в том, и в другом случае максимальное сужение не означает сужение к точке.

Естественным является желание ввести характеристики устойчивости на всем пространстве. Не вдаваясь в математические тонкости (см. о них монографию [ [ 1.15 ] ]), рассмотрим меру на пространстве такую, что мера всего пространства равна 1 (т.е. ).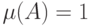

Определение 4. Абсолютным показателем устойчивости на пространстве исходных данных по мере называется число

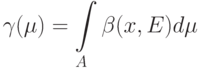
Здесь имеется в виду интеграл Лебега. Интегрирование проводится по (абстрактному) пространству исходных данных по мере . Естественно, должны быть выполнены некоторые внутриматематические условия. Читателю, незнакомому с интегрированием по Лебегу, достаточно мысленно заменить в предыдущей формуле интеграл на сумму (а пространство считать конечным, хотя и состоящим из большого числа элементов).

Определение 5. Максимальным абсолютным показателем устойчивости называется

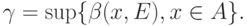
Легко видеть, что где супремум берется по всем описанным выше мерам.

Итак, построена иерархия показателей устойчивости математических моделей реальных явлений и процессов. Она с успехом использовалась в различных исследованиях, подробно развивалась, в частности, в монографии [ [ 1.15 ] ]. Приведем еще одно полезное определение.

Определение 6. Модель называется абсолютно -устойчивой, если где - максимальный абсолютный показатель устойчивости.

Пример. Если показатель устойчивости формируется с помощью метрики , совокупность допустимых отклонений - это совокупность всех окрестностей всех точек пространства исходных данных , то 0 - устойчивость модели эквивалентна непрерывности модели на множестве .

Основная проблема в общей схеме устойчивости - проверка - устойчивости данной модели относительно данной системы допустимых отклонений .

Часто оказываются полезными следующие два обобщения основной проблемы.

Проблема А ( характеризации устойчивых моделей ). Даны пространство исходных данных , пространство решений , показатель устойчивости , совокупность допустимых отклонений и неотрицательное число . Описать достаточно широкий класс - устойчивых моделей . Или: найти все - устойчивые модели среди моделей, обладающих данными свойствами, т.е. входящих в данное множество моделей.

Проблема Б ( характеризации систем допустимых отклонений ). Даны пространство исходных данных , пространство решений , показатель устойчивости , модель и неотрицательное число . Описать достаточно широкий класс систем допустимых отклонений , относительно которых модель является -устойчивой. Или: найти все такие системы допустимых отклонений среди совокупностей допустимых отклонений, обладающих данными свойствами, т.е. входящих в данное множество совокупностей допустимых отклонений.

Ясно, что проблемы А и Б можно рассматривать не только для показателя устойчивости , но и для других только что введенных показателей устойчивости, а именно, .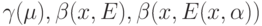

Язык общей схемы устойчивости позволяет описывать конкретные задачи специализированных теорий устойчивости в различных областях исследований, выделять основные элементы в них, ставить проблемы типа А и Б. В частности, на этом языке легко формулируются задачи теории устойчивости решений дифференциальных уравнений, теории робастности статистических процедур (см. "Оценивание" ), проблемы адекватности теории измерений, достигаемой точности расчетов в статистике интервальных данных и в логистике (см. монографию [ [ 1.15 ] ]), и т.д.

Для примера рассмотрим определение устойчивости по Ляпунову решения 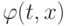нормальной автономной системы дифференциальных уравнений с начальными условиями . Здесь пространство исходных данных - конечномерное евклидово пространство, множество допустимых отклонений 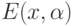окрестность радиуса точки 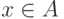, пространство решений - множество функций на луче 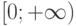с метрикой .

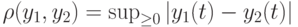Модель - отображение, переводящее начальные условия в решение системы дифференциальных уравнений с этими начальными условиями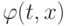

В терминах общей схемы устойчивости положение равновесия называется устойчивым по Ляпунову, если . Для формулировки определения асимптотической устойчивости по Ляпунову надо ввести в пространстве решений псевдометрику

Положение равновесия называется асимптотически устойчивым, если 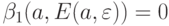для некоторого 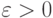где показатель устойчивости 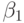рассчитан с использованием псевдометрики .

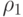Таким образом, общая схема устойчивости естественным образом включает в себя классические понятия теории устойчивости по Ляпунову. Вместе с тем стоит отметить, что эта схема дает общий подход к различным проблемам устойчивости. Она дает систему понятий, которые в каждом конкретном случае должны приспосабливаться к решаемой задаче.

До настоящего момента для определенности речь шла о допустимых отклонениях в пространстве исходных данных. Часто оказывается необходимым говорить и об отклонениях от предпосылок модели. С чисто формальной точки зрения для этого достаточно расширить понятие "исходные данные" до пары 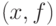, т.е. включив "прежнюю" модель в качестве второго элемента пары. Все остальные определения остаются без изменения. Теперь отклонения в пространстве решений вызываются не только отклонениями в исходных данных , но и отклонениями от предпосылок модели, т.е. отклонениями . Это соображение нам понадобится в п.6.4, посвященном робастности статистических процедур.