|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Теоретическая база прикладной статистики
4.6. Нечеткие множества как проекции случайных множеств
Нечеткость и случайность. С самого начала появления современной теории нечеткости в 1960-е годы (см.
"Различные виды статистических данных"
) началось обсуждение ее взаимоотношений с теорией вероятностей. Дело в том, что функция принадлежности нечеткого множества напоминает распределение вероятностей. Отличие состоит только в том, что сумма вероятностей по всем возможным значениям случайной величины (или интеграл, если множество возможных значений неcчетно) всегда равна 1, а сумма 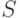 значений функции принадлежности (в непрерывном случае - интеграл от функции принадлежности) может быть любым неотрицательным числом. Возникает искушение пронормировать функцию принадлежности, т.е. разделить все ее значения на
значений функции принадлежности (в непрерывном случае - интеграл от функции принадлежности) может быть любым неотрицательным числом. Возникает искушение пронормировать функцию принадлежности, т.е. разделить все ее значения на 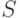 (при
(при  ), чтобы свести ее к распределению вероятностей (или к плотности вероятности).
Однако специалисты по нечеткости справедливо возражают против такого "примитивного" сведения, поскольку оно проводится отдельно для каждой размытости (нечеткого множества), и определения обычных операций над нечеткими множествами с ним согласовать нельзя. Последнее утверждение означает следующее. Пусть указанным образом преобразованы функции принадлежности нечетких множеств
), чтобы свести ее к распределению вероятностей (или к плотности вероятности).
Однако специалисты по нечеткости справедливо возражают против такого "примитивного" сведения, поскольку оно проводится отдельно для каждой размытости (нечеткого множества), и определения обычных операций над нечеткими множествами с ним согласовать нельзя. Последнее утверждение означает следующее. Пусть указанным образом преобразованы функции принадлежности нечетких множеств  и
и  . Как при этом преобразуются функции принадлежности
. Как при этом преобразуются функции принадлежности 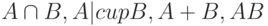 ? Установить это невозможно в принципе. Последнее утверждение становится совершенно ясным после рассмотрения нескольких примеров пар нечетких множеств с одними и теми же суммами значений функций принадлежности, но различными результатами теоретико-множественных операций над ними. Причем и суммы значений соответствующих функций принадлежности для этих результатов теоретико-множественных операций, (например, для пересечений множеств), также различны.
? Установить это невозможно в принципе. Последнее утверждение становится совершенно ясным после рассмотрения нескольких примеров пар нечетких множеств с одними и теми же суммами значений функций принадлежности, но различными результатами теоретико-множественных операций над ними. Причем и суммы значений соответствующих функций принадлежности для этих результатов теоретико-множественных операций, (например, для пересечений множеств), также различны.
В работах по нечетким множествам время от времени утверждается, что теория нечеткости является самостоятельным разделом прикладной математики и не имеет отношения к теории вероятностей (см., например, обзор литературы в монографиях [  ,
,  ]). Некоторые авторы, сравнивавшие теорию нечеткости и теорию вероятностей, подчеркивали различие между этими областями теоретических и прикладных исследований. Обычно сравнивают аксиоматику и сравнивают области приложений. Надо сразу отметить, что аргументы при втором типе сравнений не имеют доказательной силы, поскольку по поводу границ применимости даже такой давно выделившейся научной области, как вероятностно-статистические методы, имеются различные мнения. Напомним, что итог рассуждений одного из наиболее известных французских математиков Анри Лебега по поводу границ применимости арифметики таков: "Арифметика применима тогда, когда она применима" (см. его монографию [
]). Некоторые авторы, сравнивавшие теорию нечеткости и теорию вероятностей, подчеркивали различие между этими областями теоретических и прикладных исследований. Обычно сравнивают аксиоматику и сравнивают области приложений. Надо сразу отметить, что аргументы при втором типе сравнений не имеют доказательной силы, поскольку по поводу границ применимости даже такой давно выделившейся научной области, как вероятностно-статистические методы, имеются различные мнения. Напомним, что итог рассуждений одного из наиболее известных французских математиков Анри Лебега по поводу границ применимости арифметики таков: "Арифметика применима тогда, когда она применима" (см. его монографию [ 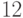 , с.21-22]).
, с.21-22]).
При сравнении различных аксиоматик теории нечеткости и теории вероятностей нетрудно увидеть, что списки аксиом различаются. Из этого, однако, отнюдь не следует, что между указанными теориями нельзя установить связь, типа известного сведения евклидовой геометрии на плоскости к арифметике (точнее к теории числовой системы  - см., например, монографию [
[
4.8
]
]). Напомним, что эти две аксиоматики - евклидовой геометрии и арифметики - на первый взгляд весьма сильно различаются.
- см., например, монографию [
[
4.8
]
]). Напомним, что эти две аксиоматики - евклидовой геометрии и арифметики - на первый взгляд весьма сильно различаются.
Можно понять желание энтузиастов теории нечеткости подчеркнуть принципиальную новизну своего научного аппарата. Однако не менее важно установить связи этого подхода с ранее известными.
Проекция случайного множества. Как оказалось, теория нечетких множеств тесно связана с теорией случайных множеств. Еще в 1975 г. в работе [ [ 4.15 ] ] было показано, что нечеткие множества естественно рассматривать как "проекции" случайных множеств. Рассмотрим этот метод сведения теории нечетких множеств к теории случайных множеств.
Определение 1. Пусть 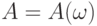 - случайное подмножество конечного множества
- случайное подмножество конечного множества  . Нечеткое множество
. Нечеткое множество  , определенное на
, определенное на  , называется проекцией
, называется проекцией  и обозначается
и обозначается  , если
, если
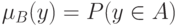 |
( 1) |
 .
.Очевидно, каждому случайному множеству  можно поставить в соответствие с помощью формулы (1) нечеткое множество
можно поставить в соответствие с помощью формулы (1) нечеткое множество  . Оказывается, верно и обратное.
. Оказывается, верно и обратное.
Теорема 1. Для любого нечеткого подмножества  конечного множества
конечного множества  существует случайное подмножество
существует случайное подмножество  множества
множества  такое, что
такое, что  .
.
Доказательство. Достаточно задать распределение случайного множества  . Пусть
. Пусть 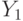 - носитель
- носитель  (см. определение 1 в п.1.4). Без ограничения общности можно считать, что
(см. определение 1 в п.1.4). Без ограничения общности можно считать, что 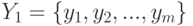 при некотором
при некотором  и элементы
и элементы 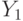 занумерованы в таком порядке, что
занумерованы в таком порядке, что
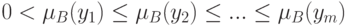

Положим

Для всех остальных подмножеств  множества
множества  положим
положим  . Поскольку элемент
. Поскольку элемент  входит во множества
входит во множества  и не входит во множества
и не входит во множества  , то из приведенных выше формул следует, что
, то из приведенных выше формул следует, что 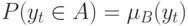 . Если
. Если 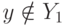 , то, очевидно,
, то, очевидно,  Теорема 1 доказана.
Теорема 1 доказана.
Распределение случайного множества с независимыми элементами, как следует из рассмотрений главы 8 монографии [ [ 2.15 ] ], полностью определяется его проекцией. Для конечного случайного множества общего вида это не так. Для уточнения сказанного понадобится следующая теорема.
Теорема 2. Для случайного подмножества  множества
множества  из конечного числа элементов наборы чисел
из конечного числа элементов наборы чисел  , и
, и 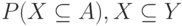 , выражаются один через другой.
, выражаются один через другой.
Доказательство. Второй набор выражается через первый следующим образом:

Элементы первого набора выразить через второй можно с помощью формулы включений и исключений из формальной логики, в соответствии с которой
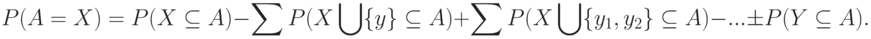
В этой формуле в первой сумме у пробегает все элементы множества  , во второй сумме переменные суммирования
, во второй сумме переменные суммирования 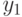 и
и 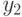 не совпадают и также пробегают это множество, и т.д. Ссылка на формулу включений и исключений завершает доказательство теоремы 2.
не совпадают и также пробегают это множество, и т.д. Ссылка на формулу включений и исключений завершает доказательство теоремы 2.
В соответствии с теоремой 2 случайное множество  можно характеризовать не только распределением, но и набором чисел
можно характеризовать не только распределением, но и набором чисел 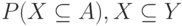 . В этом наборе
. В этом наборе 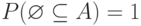 , а других связей типа равенств нет. В этот набор входят числа
, а других связей типа равенств нет. В этот набор входят числа 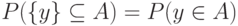 , следовательно, фиксация проекции случайного множества эквивалентна фиксации
, следовательно, фиксация проекции случайного множества эквивалентна фиксации  параметров из
параметров из 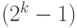 параметров, задающих распределение случайного множества
параметров, задающих распределение случайного множества  в общем случае.
в общем случае.
При доказательстве основных результатов будет использоваться следующая теорема.
Теорема 3. Если 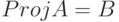 , то
, то  .
.
Для доказательства достаточно воспользоваться тождеством из теории случайных множеств  , формулой для вероятности накрытия
, формулой для вероятности накрытия  , определением отрицания нечеткого множества и тем, что сумма всех
, определением отрицания нечеткого множества и тем, что сумма всех  равна 1. При этом под формулой для вероятности накрытия имеется в виду следующее утверждение: чтобы найти вероятность накрытия фиксированного элемента
равна 1. При этом под формулой для вероятности накрытия имеется в виду следующее утверждение: чтобы найти вероятность накрытия фиксированного элемента  случайным подмножеством
случайным подмножеством 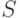 конечного множества
конечного множества 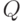 , достаточно вычислить
, достаточно вычислить
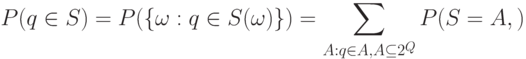
 множества
множества 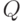 , содержащим
, содержащим  .
.Пересечения и произведения нечетких и случайных множеств. Выясним, как операции над случайными множествами соотносятся с операциями над их проекциями. В силу законов де Моргана (теорема 1 в п.1.4) и теоремы 3 достаточно рассмотреть операцию пересечения случайных множеств.
Теорема 4. Если случайные подмножества 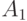 и
и 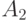 конечного множества
конечного множества  независимы, то нечеткое множество
независимы, то нечеткое множество  является произведением нечетких множеств
является произведением нечетких множеств  и
и  .
.
Доказательство. Надо показать, что для любого 
 |
( 2) |
По формуле для вероятности накрытия точки случайным множеством (см. выше)
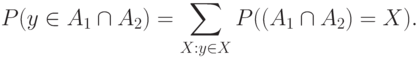 |
( 3) |
Легко проверить, что распределение пересечения случайных множеств  можно выразить через их совместное распределение следующим образом:
можно выразить через их совместное распределение следующим образом:
 |
( 4) |
Из соотношений (3) и (4) следует, что вероятность накрытия для пересечения случайных множеств можно представить в виде двойной суммы
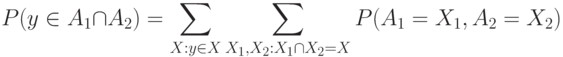 |
( 5) |
Заметим теперь, что правую часть формулы (5) можно переписать следующим образом:
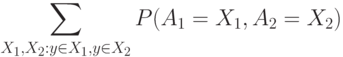 |
( 6) |
Действительно, формула (5) отличается от формулы (6) лишь тем, что в ней сгруппированы члены, в которых пересечение переменных суммирования  принимает постоянное значение. Воспользовавшись определением независимости случайных множеств и правилом перемножения сумм, получаем, что из (5) и (6) вытекает равенство
принимает постоянное значение. Воспользовавшись определением независимости случайных множеств и правилом перемножения сумм, получаем, что из (5) и (6) вытекает равенство
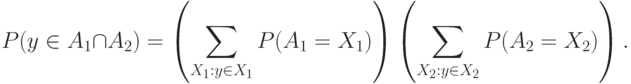
Для завершения доказательства теоремы 4 достаточно еще раз сослаться на формулу для вероятности накрытия точки случайным множеством.
Определение 2. Носителем случайного множества  называется совокупность всех тех элементов
называется совокупность всех тех элементов  , для которых
, для которых  .
.
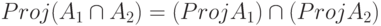
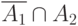 и
и  пусто.
пусто.Доказательство. Необходимо выяснить условия, при которых
 |
( 7) |
Положим
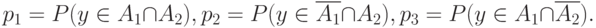
Тогда равенство (7) сводится к условию
 |
( 8) |
Ясно, что соотношение (8) выполнено тогда и только тогда, когда  при всех
при всех  , т.е. не существует ни одного элемента
, т.е. не существует ни одного элемента 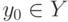 такого, что одновременно
такого, что одновременно 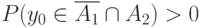 и
и 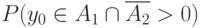 , а это эквивалентно пустоте пересечения носителей случайных множеств
, а это эквивалентно пустоте пересечения носителей случайных множеств 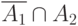 и
и  . Теорема 5 доказана.
. Теорема 5 доказана.
