|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Статистический анализ числовых величин
8.1. Оценивание основных характеристик распределения
Одна из основных задач прикладной статистики - оценивание по выборочным данным характеристик генеральной совокупности, таких, как математическое ожидание, медиана, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Точечные оценки строятся очевидным образом - используют выборочные аналоги теоретических характеристик. Для получения интервальных оценок приходится использовать асимптотическую нормальность выборочных моментов и функций от них.
Пусть исходные данные - это выборка 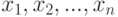 , где
, где  - объем выборки. Выборочные значения
- объем выборки. Выборочные значения 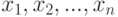 рассматриваются как реализации независимых одинаково распределенных случайных величин
рассматриваются как реализации независимых одинаково распределенных случайных величин 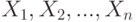 с общей функцией распределения
с общей функцией распределения 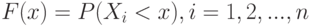 . Поскольку функция распределения произвольна (с точностью до условий регулярности типа существования моментов), то рассматриваемые задачи доверительного оценивания характеристик распределения являются непараметрическими. Существование моментов является скорее математическим ограничением, чем реальным, поскольку практически все реальные статистические данные финитны (т.е. ограничены сверху и снизу, например, шкалой прибора).
. Поскольку функция распределения произвольна (с точностью до условий регулярности типа существования моментов), то рассматриваемые задачи доверительного оценивания характеристик распределения являются непараметрическими. Существование моментов является скорее математическим ограничением, чем реальным, поскольку практически все реальные статистические данные финитны (т.е. ограничены сверху и снизу, например, шкалой прибора).
В расчетах будут использоваться выборочное среднее арифметическое

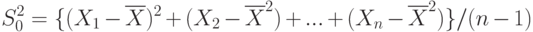
Точечное и интервальное оценивание математического ожидания. Точечной оценкой для математического ожидания в силу закона больших чисел является выборочное среднее арифметическое  . В некоторых случаях могут быть использованы и другие оценки. Например, если известно, что распределение симметрично относительно своего центра, то центр распределения является не только математическим ожиданием, но и медианой, а потому для его оценки можно использовать выборочную медиану.
. В некоторых случаях могут быть использованы и другие оценки. Например, если известно, что распределение симметрично относительно своего центра, то центр распределения является не только математическим ожиданием, но и медианой, а потому для его оценки можно использовать выборочную медиану.
Нижняя доверительная граница для математического ожидания имеет вид
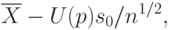
-
 - выборочное среднее арифметическое;
- выборочное среднее арифметическое; -
 - доверительная вероятность (истинное значение математического ожидания находится между нижней доверительной границей и верхней доверительной границей с вероятностью, равной доверительной);
- доверительная вероятность (истинное значение математического ожидания находится между нижней доверительной границей и верхней доверительной границей с вероятностью, равной доверительной); -
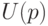 - число, заданное равенством
- число, заданное равенством  , где
, где  - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Например, при
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Например, при 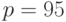 (т.е. при
(т.е. при 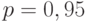 ) имеем
) имеем  . Функция
. Функция 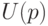 имеется в большинстве литературных источников по теории вероятностей и математической статистике (см., например, [
[
2.1
]
]);
имеется в большинстве литературных источников по теории вероятностей и математической статистике (см., например, [
[
2.1
]
]); -
 - выборочное среднее квадратическое отклонение (квадратный корень из описанной выше выборочной дисперсии).
- выборочное среднее квадратическое отклонение (квадратный корень из описанной выше выборочной дисперсии).
Верхняя доверительная граница для математического ожидания имеет вид
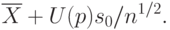
Выражения для верхней и нижней доверительных границ получены с помощью Центральной предельной теоремы теории вероятностей, теоремы о наследовании сходимости и других результатов "Теоретическая база прикладной статистики" . Они являются асимптотическими, т.е. становятся тем точнее, чем больше объем выборки. В частности, вероятность попадания истинного значения математического ожидания между нижней и верхней доверительными границами асимптотически приближается к доверительной вероятности, но, вообще говоря, может отличаться от нее. Это - недостатки непараметрического подхода. Достоинством же является то, что его можно применять всегда, когда случайная величина имеет математическое ожидание и дисперсию, что в силу финитности (ограниченности шкал) имеет быть практически всегда в реальных ситуациях.
Интересно сопоставить с параметрическим подходом. Обычно в таких случаях предполагают нормальность результатов наблюдений (которой, как уже было обосновано в
"Описание данных"
, практически никогда нет). Тогда формулы для нижней и верхней доверительных границ для математического ожидания имеют похожий вид, только вместо 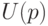 стоят квантили распределения Стьюдента (а не нормального распределения, как в приведенных выше формулах), соответствующие объему выборки. Как известно, при росте объема выборки квантили распределения Стьюдента сходятся к соответствующим квантилям стандартного нормального распределения, так что при больших объемах выборок оба подхода дают близкие результаты. Отметим, что классические доверительные интервалы несколько длиннее, поскольку квантили распределения Стьюдента больше квантилей стандартного нормального распределения, хотя это различие, на наш взгляд, и невелико.
стоят квантили распределения Стьюдента (а не нормального распределения, как в приведенных выше формулах), соответствующие объему выборки. Как известно, при росте объема выборки квантили распределения Стьюдента сходятся к соответствующим квантилям стандартного нормального распределения, так что при больших объемах выборок оба подхода дают близкие результаты. Отметим, что классические доверительные интервалы несколько длиннее, поскольку квантили распределения Стьюдента больше квантилей стандартного нормального распределения, хотя это различие, на наш взгляд, и невелико.
Пример 1. Рассмотрим данные о наработке резцов до отказа (см. 6.1, табл.6.2). Для них выборочное среднее арифметическое  (это и есть точечная оценка для математического ожидания), выборочная дисперсия
(это и есть точечная оценка для математического ожидания), выборочная дисперсия  , объем выборки
, объем выборки  . Следовательно, выборочное среднее квадратическое отклонение
. Следовательно, выборочное среднее квадратическое отклонение 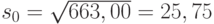 и согласно приведенным выше формулам при доверительной вероятности
и согласно приведенным выше формулам при доверительной вероятности 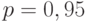 нижняя доверительная граница для математического ожидания такова:
нижняя доверительная граница для математического ожидания такова:

Если заранее известно, что результаты наблюдения имеют нормальное распределение, то нижняя и верхняя доверительная границы для математического ожидания определяются по формулам
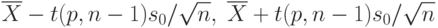
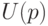 заменен на аналогичный квантиль распределения Стьюдента с
заменен на аналогичный квантиль распределения Стьюдента с 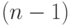 степенью свободы. Другими словами,
степенью свободы. Другими словами, 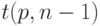 - это число, заданное равенством
- это число, заданное равенством  , где
, где  - функция распределения Стьюдента с
- функция распределения Стьюдента с 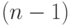 степенью свободы.
степенью свободы.Для доверительной вероятности 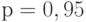 при объеме выборки
при объеме выборки  согласно [
[
2.1
]
] имеем
согласно [
[
2.1
]
] имеем 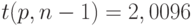 . Следовательно, нижняя доверительная граница для математического ожидания такова:
. Следовательно, нижняя доверительная граница для математического ожидания такова:

Отметим, что рассматриваемые данные согласуются с гамма-распределением (см. 7.1), а не с нормальным распределением, поэтому использование распределения Стьюдента для получения доверительных границ явно некорректно.
Иногда рекомендуют сначала проверить нормальность результатов наблюдений, а потом, в случае принятия гипотезы нормальности, рассчитывать доверительные границы с использованием квантилей распределения Стьюдента. Однако проверка нормальности - более сложная статистическая процедура, чем оценивание математического ожидания. Кроме того, применение одной статистической процедуры, как правило, нарушает предпосылки следующей процедуры, в частности, независимость результатов наблюдений (см. 7.5). Поэтому цепочка статистических процедур, следующих друг за другом, как правило, образует статистическую технологию, свойства которой неизвестны на современном уровне развития прикладной статистики.
Из сказанного вытекает, что только непараметрическую статистическую процедуру, основанную на асимптотических результатах "Теоретическая база прикладной статистики" , следует применять для анализа реальных данных. Как правило, встречающиеся на практике распределения не являются нормальными (см. 5.1), а потому применение квантилей распределения Стьюдента неправомерно.
Точечное и интервальное оценивание медианы. Точечной оценкой для медианы является выборочная медиана.
Пример 2. Для данных о наработке резцов до отказа объем выборки - четное число, поэтому выборочной медианой является полусумма 25-го и 26-го членов вариационного ряда, т.е. (56 + 56,5)/2 = 56,25.
Чтобы построить доверительные границы для медианы, по доверительной вероятности  находят
находят 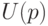 , как разъяснено выше. Затем вычисляют натуральное число
, как разъяснено выше. Затем вычисляют натуральное число
![C(p)=[n/2-U(p)n^{1/2}/2]](/sites/default/files/tex_cache/28aa233e9bc3c93de7b1031c31ecbd6c.png)
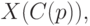
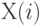 - член вариационного ряда с номером
- член вариационного ряда с номером  , построенного по исходной выборке (т.е.
, построенного по исходной выборке (т.е.  -я порядковая статистика). Верхняя доверительная граница для медианы имеет вид
-я порядковая статистика). Верхняя доверительная граница для медианы имеет вид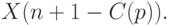
Пример 3. Для данных о наработке резцов до отказа  . Рассмотрим как обычно, доверительную вероятность
. Рассмотрим как обычно, доверительную вероятность 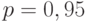 . Тогда
. Тогда
![C(p)=[50/2-1,96\sqrt{50}/2]=[18,07]=18.](/sites/default/files/tex_cache/8e37ec54ba483aebf81eba6df5e204d3.png)
Следовательно, нижней доверительной границей является  , а верхней доверительной границей
, а верхней доверительной границей 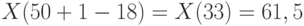 .
.
Поскольку в случае нормального распределения медиана совпадает с математическим ожиданием, то каких-либо специальных способов ее оценивания в классическом случае нет.
Точечное и интервальное оценивание дисперсии. Точечной оценкой дисперсии является выборочная дисперсия 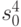 . Эта оценка является несмещенной и состоятельной. Доверительные границы находятся с помощью величины
. Эта оценка является несмещенной и состоятельной. Доверительные границы находятся с помощью величины
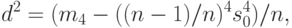
где 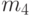 - выборочный четвертый центральный момент, т.е.
- выборочный четвертый центральный момент, т.е.  .
.
Нижняя доверительная граница для дисперсии случайной величины имеет вид

-
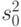 - выборочная дисперсия,
- выборочная дисперсия, -
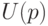 - квантиль нормального распределения порядка
- квантиль нормального распределения порядка  (как и раньше),
(как и раньше), -
 - положительный квадратный корень из величины
- положительный квадратный корень из величины 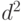 , введенной выше.
, введенной выше.
Верхняя доверительная граница для дисперсии случайной величины имеет вид

При выводе приведенных соотношений используется асимптотическая нормальность выборочной дисперсии, установленная, например, в учебнике по математической статистике [
[
8.2
]
, с.419]. Соответственно доверительный интервал является непараметрическим и асимптотическим. В классическом случае точечная оценка имеет тот же вид, а вот доверительные границы находят с помощью квантилей распределения хи-квадрат с числом степеней свободы, на 1 меньшим объема выборки. Отметим, что в случае нормального распределения четвертый момент в 3 раза больше квадрата дисперсии, а потому можно оценить 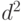 как
как 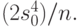 Это дает быстрый способ для интервальной оценки дисперсии в нормальном случае.
Это дает быстрый способ для интервальной оценки дисперсии в нормальном случае.
Пример 4. Для данных о наработке резцов до отказа объем выборки  , выборочная дисперсия
, выборочная дисперсия  , четвертый выборочный момент
, четвертый выборочный момент  . Поэтому
. Поэтому

Тогда 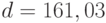 . Для доверительной вероятности
. Для доверительной вероятности 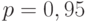 нижняя доверительная граница для дисперсии случайной величины такова:
нижняя доверительная граница для дисперсии случайной величины такова:

Пример 5. В случае нормального распределения с целью быстрого получения доверительного интервала величина 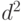 оценивается как
оценивается как
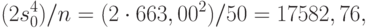
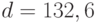 . Для доверительной вероятности
. Для доверительной вероятности 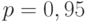 нижняя доверительная граница для дисперсии заменяется на
нижняя доверительная граница для дисперсии заменяется на
Сужение границ для дисперсии вполне естественно. Данные о наработке резцов до предельного состояния (т.е. до отказа) соответствуют гамма-распределению, а это распределение является асимметричным, с "тяжелым" правым "хвостом". Последнее означает, что плотность убывает заметно медленнее, чем для нормального распределения. Как следствие, четвертый момент заметно больше, чем для нормального распределения с теми же математическим ожиданием и дисперсией. А потому больше и параметр  . Из проведенных расчетов видно, что использование алгоритмов расчетов, соответствующих нормальному распределению, в ситуации, когда распределение результатов наблюдений отлично от нормального, может привести к заметно искаженным выводам.
. Из проведенных расчетов видно, что использование алгоритмов расчетов, соответствующих нормальному распределению, в ситуации, когда распределение результатов наблюдений отлично от нормального, может привести к заметно искаженным выводам.
Пример 6. В классическом случае нормального распределения исходят из того, что величина 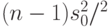 имеет распределение хи-квадрат с
имеет распределение хи-квадрат с 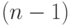 степенью свободы. Для доверительной вероятности
степенью свободы. Для доверительной вероятности 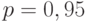 следует рассмотреть неравенство
следует рассмотреть неравенство
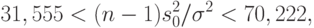
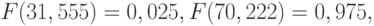
 - функция хи-квадрат распределения с 49 степенями свободы. Следовательно, нижняя доверительная граница для дисперсии нормально распределенной случайной величины такова:
- функция хи-квадрат распределения с 49 степенями свободы. Следовательно, нижняя доверительная граница для дисперсии нормально распределенной случайной величины такова: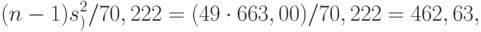

Полученный доверительный интервал не является симметричным относительно точечной оценки. Нижняя доверительная граница больше, чем в примерах 4 и 5, но и верхняя доверительная граница тоже больше. Несимметричность доверительного интервала в примере 6 приводит к тому, что его трудно сопоставить с симметричными интервалами примеров 4 и 5. Что же касается практических рекомендаций, то они однозначны: поскольку обычно нет основания считать данные имеющими нормальное распределение, то при анализе реальных данных надо пользоваться непараметрическими методами, не предполагающими нормальность, т.е. методами, примененными в примере 4.
Точечное и интервальное оценивание среднего квадратического отклонения. Точечной оценкой является выборочное среднее квадратическое отклонение, т.е. неотрицательный квадратный корень из выборочной дисперсии. Дисперсия рассматриваемой случайной величины - выборочного среднего квадратического отклонения  - оценивается как дробь
- оценивается как дробь
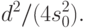
Нижняя доверительная граница для среднего квадратического отклонения исходной случайной величины имеет вид
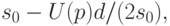
-
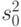 - выборочная дисперсия,
- выборочная дисперсия, -
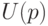 - квантиль нормального распределения порядка
- квантиль нормального распределения порядка  (как и раньше),
(как и раньше), -
 - положительный квадратный корень из величины
- положительный квадратный корень из величины 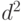 , введенной выше при оценивании дисперсии.
, введенной выше при оценивании дисперсии.
Верхняя доверительная граница для среднего квадратического отклонения исходной случайной величины имеет вид
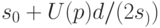
Пример 7. Для данных о наработке резцов до отказа точечной оценкой для среднего квадратического отклонения является 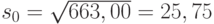 . При доверительной вероятности
. При доверительной вероятности 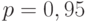 нижняя доверительная граница такова:
нижняя доверительная граница такова:
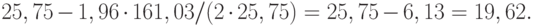
Соответственно верхняя доверительная граница симметрична нижней относительно точечной оценки и равна 25,75+6,13=31,88.
Правила интервального оценивания для среднего квадратического отклонения получены из аналогичных правил для оценивания дисперсии с помощью метода линеаризации (см. "Теоретическая база прикладной статистики" или, например, [ [ 1.15 ] , п.2.4]). Как и раньше, доверительный интервал является симметричным, непараметрическим и асимптотическим.
Поскольку среднее квадратическое отклонение - это квадратный корень их дисперсии, то доверительные границы можно получить, извлекая квадратные корни из одноименных границ для дисперсии.
Пример 8. Для данных о наработке резцов до отказа при доверительной вероятности 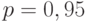 согласно примеру 4 доверительный интервал для дисперсии - это [347,37; 978,63]. Извлекая квадратные корни, получаем доверительный интервал [18,64; 31,28] для среднего квадратического отклонения, соответствующий тому же значению доверительной вероятности. Он не является симметричным относительно точечной оценки. Его длина 12,64 несколько больше длины симметричного доверительного интервала 12,26 в примере 7.
согласно примеру 4 доверительный интервал для дисперсии - это [347,37; 978,63]. Извлекая квадратные корни, получаем доверительный интервал [18,64; 31,28] для среднего квадратического отклонения, соответствующий тому же значению доверительной вероятности. Он не является симметричным относительно точечной оценки. Его длина 12,64 несколько больше длины симметричного доверительного интервала 12,26 в примере 7.
Классический подход, основанный на гипотезе нормальности распределения результатов наблюдения, связан с использованием распределения хи-квадрат и сводится к извлечению квадратных корней из доверительных границ для дисперсии.
Пример 9. Применяя формально классический подход к данным о наработке резцов до отказа, исходим из доверительного интервала для дисперсии [462,63; 1029,54], соответствующего доверительной вероятности 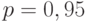 . Извлекая квадратные корни, находим доверительный интервал для среднего квадратического отклонения [21,51; 32,09]. Как и следовало ожидать, длина 10,58 этого несимметричного интервала меньше длины непараметрического доверительного интервала.
. Извлекая квадратные корни, находим доверительный интервал для среднего квадратического отклонения [21,51; 32,09]. Как и следовало ожидать, длина 10,58 этого несимметричного интервала меньше длины непараметрического доверительного интервала.
Точечное и интервальное оценивание коэффициента вариации. Коэффициент вариации  широко используется при анализе конкретных технических, экономических, социологических, медицинских и иных данных (поскольку они, как правило, положительны), но не очень популярен среди теоретиков в области математической статистики. Точечной оценкой теоретического коэффициента вариации
широко используется при анализе конкретных технических, экономических, социологических, медицинских и иных данных (поскольку они, как правило, положительны), но не очень популярен среди теоретиков в области математической статистики. Точечной оценкой теоретического коэффициента вариации  является выборочный коэффициент вариации
является выборочный коэффициент вариации

Дисперсия выборочного коэффициента вариации состоятельно оценивается с помощью вспомогательной величины
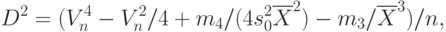
-
 - выборочное среднее арифметическое,
- выборочное среднее арифметическое, -
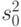 - выборочная дисперсия,
- выборочная дисперсия, -
 - выборочный третий центральный момент, т.е.
- выборочный третий центральный момент, т.е.
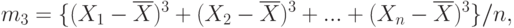
-
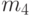 - выборочный четвертый центральный момент (см. выше),
- выборочный четвертый центральный момент (см. выше), -
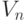 - выборочный коэффициент вариации,
- выборочный коэффициент вариации, -
 - объем выборки.
- объем выборки.
Нижняя доверительная граница для (теоретического) коэффициента вариации исходной случайной величины имеет вид

-
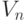 - выборочный коэффициент вариации,
- выборочный коэффициент вариации, -
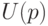 - квантиль нормального распределения порядка
- квантиль нормального распределения порядка 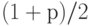 (как и ранее),
(как и ранее), -
 - положительный квадратный корень из величины
- положительный квадратный корень из величины  , введенной выше.
, введенной выше.
Верхняя доверительная граница для (теоретического) коэффициента вариации исходной случайной величины имеет вид
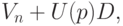
Как и в предыдущих случаях, доверительный интервал является непараметрическим и асимптотическим. Он получен в результате применения специальной технологии вывода асимптотических соотношений прикладной статистики (см. "Теоретическая база прикладной статистики" ). Напомним, что эта технология в качестве первого шага использует многомерную центральную предельную теорему, примененную к сумме векторов, координаты которых - степени исходных случайных величин. Второй шаг - преобразование предельного многомерного нормального вектора с целью получения интересующего исследователя вектора. При этом используются соображения линеаризации и отбрасываются бесконечно малые величины. Третий шаг - строгое обоснование полученных результатов на стандартном для асимптотических математико-статистических рассуждений уровне. При этом обычно приходится использовать необходимые и достаточные условия наследования сходимости, полученные в монографии [ [ 1.15 ] , п.2.4]. Именно таким образом были получены приведенные выше результаты для выборочного коэффициента вариации. Формулы оказались существенно более сложными, чем в предыдущих случаях. Это объясняется тем, что выборочный коэффициент вариации - функция двух выборочных моментов, а ранее рассматривались либо выборочные моменты поодиночке, либо функция от одного выборочного момента - выборочной дисперсии.
Пример 10. Для данных о наработке резцов до отказа выборочное среднее арифметическое  , выборочная дисперсия
, выборочная дисперсия  , выборочное среднее квадратическое отклонение
, выборочное среднее квадратическое отклонение  , выборочный третий центральный момент
, выборочный третий центральный момент  , выборочный четвертый центральный момент
, выборочный четвертый центральный момент  . Следовательно, выборочный коэффициент вариации таков:
. Следовательно, выборочный коэффициент вариации таков:
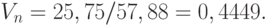
Рассчитаем значение вспомогательной величины
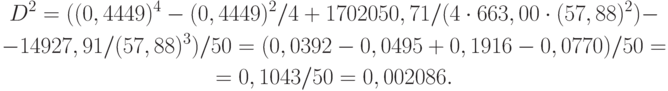
Следовательно, 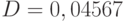 . При доверительной вероятности
. При доверительной вероятности 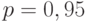 нижняя доверительная граница для теоретического коэффициента вариации имеет вид
нижняя доверительная граница для теоретического коэффициента вариации имеет вид
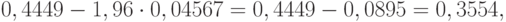

Среди классических результатов математической статистики, основанных на гипотезе нормальности результатов наблюдений, нет методов построения доверительных границ для коэффициента вариации, поскольку задача построения таких границ не выражается в терминах обычно используемых распределений, например, распределений Стьюдента и хи-квадрат.
Примеры применения доверительных границ для коэффициентов вариации при решении прикладных задач приведены, например, в работе [ [ 8.9 ] ], посвященной анализу технических характеристик и показателей качества.
