Статистический анализ числовых величин

8.4. Состоятельные критерии проверки однородности независимых выборок

В соответствии с методологией прикладной статистики естественно потребовать, чтобы рекомендуемый для массового использования в технических, экономических, медицинских и иных исследованиях критерий однородности был состоятельным. Напомним: это значит, что для любых отличных друг от друга функций распределения и 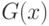(другими словами, при справедливости альтернативной гипотезы ) вероятность отклонения гипотезы должна стремиться к 1 при увеличении объемов выборок т и п. Из перечисленных выше (в конце 8.2) критериев однородности состоятельными являются только критерии Смирнова и типа омега-квадрат.

Проведенное исследование мощности (методом статистических испытаний) первых четырех из перечисленных выше критериев (при различных вариантах функций распределения и 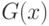) подтвердило преимущество критериев Смирнова и омега-квадрат и при объемах выборок 6-12. Рассмотрим эти критерии подробнее.

Критерий Смирнова однородности двух независимых выборок. Он предложен членом-корреспондентом АН СССР Н.В. Смирновым в 1939 г. (см. справочник [ [ 2.1 ] ]). Единственное ограничение - функции распределения и 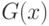должны быть непрерывными. Напомним, что согласно Л.Н. Большеву и Н.В. Смирнову [ [ 2.1 ] ] значение эмпирической функции распределения в точке равно доле результатов наблюдений в выборке, меньших . 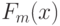Критерий Смирнова основан на использовании эмпирических функций распределения и , построенных по первой и второй выборкам соответственно. Значение статистики Смирнова

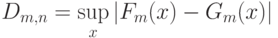
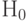сравнивают с соответствующим критическим значением (см., например, [ [ 2.1 ] ]) и по результатам сравнения принимают или отклоняют гипотезу о совпадении (однородности) функций распределения. Практически значение статистики 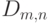рекомендуется, согласно [ [ 2.1 ] ], вычислять по формулам

где - элементы первой выборки 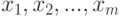, переставленные в порядке возрастания, а 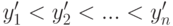- элементы второй выборки 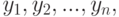также переставленные в порядке возрастания. Поскольку функции распределения и 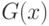предполагаются непрерывными, то вероятность совпадения каких-либо выборочных значений равна 0.

Разработаны алгоритмы и программы для ЭВМ, позволяющие рассчитывать точные распределения, процентные точки и достигаемый уровень значимости для двухвыборочной статистики Смирнова 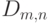, а также подробные таблицы (см., например, методику [6], содержащую описание алгоритмов, тексты программ и подробные таблицы).

Однако у критерия Смирнова есть и недостатки. Его распределение сосредоточено в сравнительно небольшом числе точек, поэтому функция распределения растет большими скачками. В результате не удается выдержать заданный уровень значимости. Реальный уровень значимости может в несколько раз отличаться от номинального (подробному обсуждению неклассического феномена существенного отличия реального уровня значимости от номинального посвящена работа [ [ 2.4 ] ]).

Критерий типа омега-квадрат (Лемана-Розенблатта). Статистика критерия типа омега-квадрат для проверки однородности двух независимых выборок имеет вид:

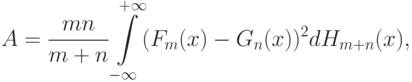
где - эмпирическая функция распределения, построенная по объединенной выборке. Легко видеть, что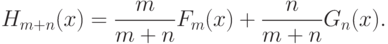

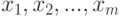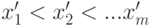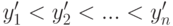Статистика типа омега-квадрат была предложена Э. Леманом в 1951 г., изучена в 1952 г. М. Розенблаттом, а затем и другими исследователями. Она зависит лишь от рангов элементов двух выборок в объединенной выборке. Пусть - первая выборка, - соответствующий вариационный ряд, - вторая выборка, - вариационный ряд, соответствующий второй выборке. Поскольку функции распределения независимых выборок непрерывны, то с вероятностью 1 все выборочные значения различны, совпадения отсутствуют. Статистика представляется в виде (см., например, [ [ 2.1 ] ]):

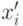где - ранг и 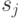- ранг в общем вариационном ряду, построенном по объединенной выборке.

Правила принятия решений при проверке однородности двух выборок на основе статистик Смирнова и типа омега-квадрат, т.е. таблицы критических значений в зависимости от уровней значимости и объемов выборок, приведены, например, в [ [ 2.1 ] ].

Рекомендации по выбору критерия однородности. Для критерия типа омега-квадрат нет выраженного эффекта различия между номинальными и реальными уровнями значимости. Поэтому мы рекомендуем для проверки однородности функций распределения (гипотеза ) применять статистику типа омега-квадрат. Если методическое, табличное или программное обеспечение для статистики Лемана - Розенблатта отсутствует, рекомендуем использовать критерий Смирнова. Для проверки однородности математических ожиданий (гипотеза ) целесообразно применять критерий Крамера-Уэлча. По нашему мнению, статистики Стьюдента, Вилкоксона и др. допустимо использовать лишь в отдельных частных случаях, рассмотренных выше.

Некоторые соображения о внедрении современных методов прикладной статистики в практику технических, экономических, медицинских и иных исследований. Даже из проведенного выше разбора лишь одной из типичных статистических задач - задачи проверки однородности двух независимых выборок - можно сделать вывод о целесообразности широкого развертывания работ по критическому анализу сложившейся практики статистической обработки данных и по внедрению накопленного арсенала современных методов прикладной статистики. По нашему мнению, широкого внедрения заслуживают, в частности, методы многомерного статистического анализа, планирования эксперимента, статистики объектов нечисловой природы. Очевидно, рассматриваемые работы должны быть плановыми, организационно оформленными, проводиться мощными самостоятельными организациями и подразделениями. Целесообразно создание службы статистических консультаций в системе научно-исследовательских учреждений и вузов технического, экономического, медицинского профиля.