|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Статистический анализ числовых величин
8.3. Двухвыборочный критерий Вилкоксона
Покажем (и это - основной результат настоящего параграфа), что двухвыборочный критерий Вилкоксона (в литературе его называют также критерием Манна-Уитни) предназначен для проверки гипотезы

 - случайная величина, распределенная как элементы первой выборки, а
- случайная величина, распределенная как элементы первой выборки, а  - второй.
- второй.В описанной выше вероятностной модели двух независимых выборок без ограничения общности можно считать, что объем первой из них не превосходит объема второй,  , в противном случае выборки можно поменять местами. Обычно предполагается, что функции
, в противном случае выборки можно поменять местами. Обычно предполагается, что функции  и
и 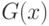 непрерывны и строго возрастают. Из непрерывности этих функций следует, что с вероятностью 1 все
непрерывны и строго возрастают. Из непрерывности этих функций следует, что с вероятностью 1 все  результатов наблюдений различны. В реальных эконометрических данных иногда встречаются совпадения, но сам факт их наличия - свидетельство нарушений предпосылок только что описанной базовой математической модели.
результатов наблюдений различны. В реальных эконометрических данных иногда встречаются совпадения, но сам факт их наличия - свидетельство нарушений предпосылок только что описанной базовой математической модели.
Статистика  двухвыборочного критерия Вилкоксона определяется следующим образом. Все элементы объединенной выборки
двухвыборочного критерия Вилкоксона определяется следующим образом. Все элементы объединенной выборки  упорядочиваются в порядке возрастания. Элементы первой выборки
упорядочиваются в порядке возрастания. Элементы первой выборки 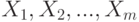 занимают в общем вариационном ряду места с номерами
занимают в общем вариационном ряду места с номерами 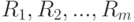 , другими словами, имеют ранги
, другими словами, имеют ранги 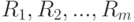 . Тогда статистика Вилкоксона - это сумма рангов элементов первой выборки
. Тогда статистика Вилкоксона - это сумма рангов элементов первой выборки
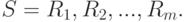
Статистика  Манна-Уитни определяется как число пар
Манна-Уитни определяется как число пар  таких, что
таких, что  среди всех
среди всех 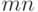 пар, в которых первый элемент - из первой выборки, а второй - из второй. Как известно [
[
8.3
]
, с.160],
пар, в которых первый элемент - из первой выборки, а второй - из второй. Как известно [
[
8.3
]
, с.160],

Поскольку  и
и  линейно связаны, то часто говорят не о двух критериях - Вилкоксона и Манна-Уитни, а об одном - критерии Вилкоксона (Манна-Уитни).
линейно связаны, то часто говорят не о двух критериях - Вилкоксона и Манна-Уитни, а об одном - критерии Вилкоксона (Манна-Уитни).
Критерий Вилкоксона - один из самых известных инструментов непараметрической статистики (наряду со статистиками типа Колмогорова-Смирнова и коэффициентами ранговой корреляции). Свойствам этого критерия и таблицам его критических значений уделяется место во многих монографиях по математической и прикладной статистике (см., например, [ [ 2.1 ] , [ 8.3 ] , [ 8.11 ] ]).
Однако в литературе имеются и неточные утверждения относительно возможностей критерия Вилкоксона. Так, одни полагают, что с его помощью можно обнаружить любое различие между функциями распределения  и
и 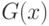 . По мнению других, этот критерий нацелен на проверку равенства медиан распределений, соответствующих выборкам. И то, и другое, строго говоря, неверно. Это будет ясно из дальнейшего изложения.
. По мнению других, этот критерий нацелен на проверку равенства медиан распределений, соответствующих выборкам. И то, и другое, строго говоря, неверно. Это будет ясно из дальнейшего изложения.
Введем некоторые обозначения. Пусть 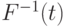 - функция, обратная к функции распределения
- функция, обратная к функции распределения  . Она определена на отрезке [0;1]. Положим
. Она определена на отрезке [0;1]. Положим 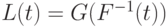 . Поскольку
. Поскольку  непрерывна и строго возрастает, то
непрерывна и строго возрастает, то 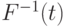 и
и 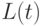 обладают теми же свойствами. Важную роль в дальнейшем изложении будет играть величина
обладают теми же свойствами. Важную роль в дальнейшем изложении будет играть величина  Как нетрудно показать,
Как нетрудно показать,
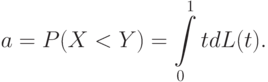
Введем также параметры
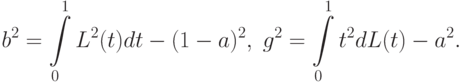
Тогда математические ожидания и дисперсии статистик Вилкоксона и Манна-Уитни согласно [ [ 8.3 ] , с.160] выражаются через введенные величины:
![\begin{gathered}
М(U) = mna, М(S) = mn + m(m+1)/2 - М(U) = mn(1- a) + m(m+1)/2,\\
D(S) = D(U) = mn [(n - 1) b^2 + (m - 1) g^2 + a(1 - a)].
\end{gathered}](/sites/default/files/tex_cache/abe905c6e923360c988caf7d8be33187.png) |
( 1) |
Когда объемы обеих выборок безгранично растут, распределения статистик Вилкоксона и Манна-Уитни являются асимптотически нормальными (см., например, [ [ 8.3 ] , гл. 5 и [ 2.10 ] ]) с параметрами, задаваемыми формулами (1).
Если выборки полностью однородны, т.е. их функции распределения совпадают, справедлива гипотеза
 |
( 2) |
 для
для  из отрезка
из отрезка ![[0, 1], L(t)= 0](/sites/default/files/tex_cache/1442eeced8e48c99f750d4016a76ea19.png) для всех отрицательных
для всех отрицательных  и
и  для
для  , соответственно
, соответственно 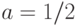 . Подставляя в формулы (1), получаем, что
. Подставляя в формулы (1), получаем, что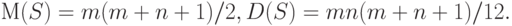 |
( 3) |
Следовательно, распределение нормированной и центрированной статистики Вилкоксона
 |
( 4) |
Из асимптотической нормальности статистики  следует, что правило принятия решения для критерия Вилкоксона выглядит следующим образом:
следует, что правило принятия решения для критерия Вилкоксона выглядит следующим образом:
- если
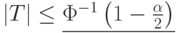 , то гипотеза (2) однородности (тождества) функций распределений принимается на уровне значимости
, то гипотеза (2) однородности (тождества) функций распределений принимается на уровне значимости  ;
; - если же
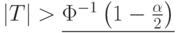 , то гипотеза (2) однородности (тождества) функций распределений отклоняется на уровне значимости
, то гипотеза (2) однородности (тождества) функций распределений отклоняется на уровне значимости  .
.
В прикладной статистике наиболее часто применяется уровень значимости  . Тогда значение модуля статистики
. Тогда значение модуля статистики  Вилкоксона надо сравнивать с граничным значением
Вилкоксона надо сравнивать с граничным значением 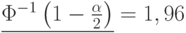 .
.
Пример 1. Пусть даны две выборки. Первая содержит  элементов 17; 22; 3; 5; 15; 2; 0; 7; 13; 97; 66; 14. Вторая содержит
элементов 17; 22; 3; 5; 15; 2; 0; 7; 13; 97; 66; 14. Вторая содержит 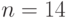 элементов 47; 30; 2; 15; 1; 21; 25; 7; 44; 29; 33; 11; 6; 15. Проведем проверку однородности функций распределения двух выборок с помощью критерия Вилкоксона.
элементов 47; 30; 2; 15; 1; 21; 25; 7; 44; 29; 33; 11; 6; 15. Проведем проверку однородности функций распределения двух выборок с помощью критерия Вилкоксона.
Первым шагом является построение общего вариационного ряда для элементов двух выборок (табл.8.1).
| Ранги | 1 | 2 | 3,5 | 3,5 | 5 | 6 | 7 | 8,5 | 8,5 | 10 | 11 | 12 | 14 |
| Элементы выборок | 0 | 1 | 2 | 2 | 3 | 5 | 6 | 7 | 7 | 11 | 13 | 14 | 15 |
| Номера выборок | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 1 | 2 | 2 | 1 | 1 | 1 |
| Ранги | 14 | 14 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| Элементы выборок | 15 | 15 | 17 | 21 | 22 | 25 | 29 | 30 | 33 | 44 | 47 | 66 | 97 |
| Номера выборок | 2 | 2 | 1 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 |
Хотя с точки зрения теории математической статистики вероятность совпадения двух элементов выборок равна 0, в реальных выборках экономических данных совпадения встречаются. Так, в рассматриваемых выборках, как видно из табл.8.1, два раза повторяется величина 2, два раза - величина 7 и три раза - величина 15. В таких случаях говорят о наличии "связанных рангов", а соответствующим совпадающим величинам приписывают среднее арифметическое тех рангов, которые они занимают. Так, величины 2 и 2 занимают в объединенной выборке места 3 и 4, поэтому им приписывается ранг (3+4)/2 = 3,5. Величины 7 и 7 занимают в объединенной выборке места 8 и 9, поэтому им приписывается ранг (8+9)/2 = 8,5. Величины 15, 15 и 15 занимают в объединенной выборке места 13, 14 и 15, поэтому им приписывается ранг (13+14+15)/3 = 14.
Следующий шаг - подсчет значения статистики Вилкоксона, т.е. суммы рангов элементов первой выборки
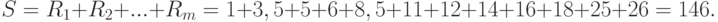
Подсчитаем также сумму рангов элементов второй выборки
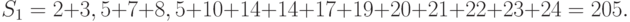
Величина  может быть использована для контроля вычислений. Дело в том, что суммы рангов элементов первой выборки
может быть использована для контроля вычислений. Дело в том, что суммы рангов элементов первой выборки  и второй выборки
и второй выборки  вместе составляют сумму рангов объединенной выборки, т.е. сумму всех натуральных чисел от 1 до
вместе составляют сумму рангов объединенной выборки, т.е. сумму всех натуральных чисел от 1 до  . Следовательно,
. Следовательно,

В соответствии с ранее проведенными расчетами  . Необходимое условие правильности расчетов выполнено. Это условие не является достаточным и не гарантирует правильности расчетов.
. Необходимое условие правильности расчетов выполнено. Это условие не является достаточным и не гарантирует правильности расчетов.
Перейдем к расчету статистики  . Согласно формуле (3)
. Согласно формуле (3)
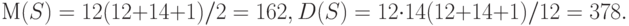
Следовательно,

Поскольку  , то гипотеза однородности принимается на уровне значимости 0,05.
, то гипотеза однородности принимается на уровне значимости 0,05.
Что будет, если поменять выборки местами, вторую назвать первой? Тогда вместо  надо рассматривать
надо рассматривать  . Имеем
. Имеем
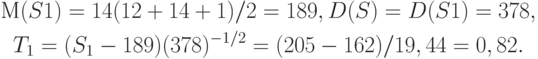
Таким образом, значения статистики критерия отличаются только знаком (можно показать, что это утверждение верно всегда). Поскольку в правиле принятия решения используется только абсолютная величина статистики, то принимаемое решение не зависит от того, какую выборку считаем первой, а какую второй. Для уменьшения объема таблиц принято считать первой выборку меньшего объема.
Продолжим обсуждение критерия Вилкоксона. Правила принятия решений и таблица критических значений для критерия Вилкоксона строятся в предположении справедливости гипотезы полной однородности, описываемой формулой (2). А что будет, если эта гипотеза неверна? Другими словами, какова мощность критерия Вилкоксона?
Пусть объемы выборок достаточно велики, так что можно пользоваться асимптотической нормальностью статистики Вилкоксона. Тогда в соответствии с формулами (1) статистика T будет асимптотически нормальна с параметрами
![\begin{aligned}
&М(T) = (12mn)^{1/2}(1/2-a)(m+n+1)^{-1/2}, \\
&D(T)= 12 [(n - 1) b^2 + (m - 1) g^2 + a(1 - a) ] (m+n+1)^{-1}.
\end{aligned}](/sites/default/files/tex_cache/ee3fe904bff633f01096bad0ac105a36.png) |
( 5) |
Из формул (5) видно большое значение гипотезы
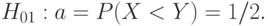 |
( 6) |
Если эта гипотеза неверна, то, поскольку  , справедлива оценка
, справедлива оценка
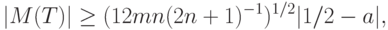
 безгранично растет при росте объемов выборок. В то же время, поскольку
безгранично растет при росте объемов выборок. В то же время, поскольку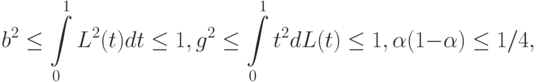
^{-1}\le 12.](/sites/default/files/tex_cache/9eacc77aae40d9088ff49c4e2a60e2f2.png) |
( 7) |
Следовательно, вероятность отклонения гипотезы 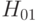 , когда она неверна, т.е. мощность критерия Вилкоксона как критерия проверки гипотезы (6), стремится к 1 при возрастании объемов выборок, т.е. критерий Вилкоксона является состоятельным для этой гипотезы при альтернативе
, когда она неверна, т.е. мощность критерия Вилкоксона как критерия проверки гипотезы (6), стремится к 1 при возрастании объемов выборок, т.е. критерий Вилкоксона является состоятельным для этой гипотезы при альтернативе
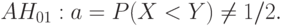 |
( 8) |
 асимптотически нормальна с математическим ожиданием 0 и дисперсией, определяемой формулой
асимптотически нормальна с математическим ожиданием 0 и дисперсией, определяемой формулой^{-1}.](/sites/default/files/tex_cache/8724996f2b0e9b89cb25a95a34328dbb.png) |
( 9) |
Гипотеза (6) является сложной, дисперсия (9), как показывают приводимые ниже примеры, в зависимости от значений 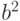 и
и 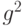 может быть как больше 1, так и меньше 1, но согласно неравенству (7) никогда не превосходит 12.
может быть как больше 1, так и меньше 1, но согласно неравенству (7) никогда не превосходит 12.
