Компьютеры в прикладной статистике

Методы размножения выборок (бутстреп-методы). Прикладная статистика бурно развивается последние десятилетия. Серьезным (хотя, разумеется, не единственным и не главным) стимулом является стремительно растущая производительность вычислительных средств. Поэтому понятен острый интерес к статистическим методам, интенсивно использующим компьютеры. Одним из таких методов является так называемый "бутстреп", предложенный в 1977 г. Б.Эфроном из Станфордского университета (США).

Сам термин "бутстреп" произошел от английского слова " bootstrap ". Оно буквально означает что-то вроде: "вытягивание себя (из болота) за шнурки от ботинок". Термин специально придуман и заставляет вспомнить о подвигах барона Мюнхгаузена.

В истории прикладной статистики было несколько более или менее успешно осуществленных рекламных кампаний. В каждой из них "раскручивался" тот или иной метод, который, как правило, отвечал нескольким условиям:

• по мнению его пропагандистов, полностью решал актуальную научную задачу;
• был понятен (при постановке задачи, ее решении и интерпретации результатов) широким массам потенциальных пользователей;
• использовал современные возможности вычислительной техники.

Пропагандисты метода, как правило, избегали беспристрастного сравнения его возможностей с возможностями иных методов прикладной статистики. Если сравнения и проводились, то с заведомо слабым "противником".

В нашей стране в условиях отсутствия систематического образования в области прикладной статистики подобные рекламные кампании находили особо благоприятную почву, поскольку у большинства затронутых ими специалистов не было достаточных знаний в области методологии построения моделей прикладной статистики для того, чтобы составить самостоятельное квалифицированное мнение.

Речь идет о таких методах и постановках, как бутстреп, нейронные сети, метод группового учета аргументов, робастные оценки по Тьюки-Хуберу, асимптотика пропорционального роста числа параметров и объема данных и др. Бывают локальные всплески энтузиазма, например, московские социологи в 1980-х годах пропагандировали так называемый "детерминационный анализ" - простой эвристический метод анализа таблиц сопряженности. Хотя в Новосибирске в это время давно уже было разработано продвинутое математическое и программное обеспечение анализа векторов разнотипных признаков, включающее в себя "детерминационный анализ" как весьма частный случай.

Однако даже на фоне всех остальных рекламных кампаний судьба бутстрепа исключительна. Во-первых, признанный его автор Б. Эфрон с самого начала признавался, что он ничего принципиально нового не сделал. Его исходная статья (первая в сборнике [ [ 13.49 ] ]) называлась: "Бутстреп-методы: новый взгляд на методы складного ножа". Тем самым Б. Эфрон честно признавал первенство за М. Кенуем - автором методов "складного ножа". Во вторых, сразу появились статьи и дискуссии в научных изданиях, публикации рекламного характера, и даже в научно-популярных журналах. Бурные обсуждения на конференциях, спешный выпуск книг. В 1980-е годы финансовая подоплека всей этой активности, связанная с выбиванием грантов на научную деятельность, содержание учебных заведений и т.п. была мало понятна отечественным специалистам.

В чем заключается основная идея группы методов "размножения выборок", наиболее известным представителем которых является бутстреп?

Пусть дана выборка 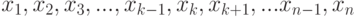. В вероятностно-статистической теории предполагаем, что это - набор независимых одинаково распределенных случайных величин. Пусть эконометрика интересует некоторая статистика . Как изучить ее свойства? Подобными проблемами мы занимались на протяжении всего курса и знаем, насколько это непросто. Идея, которую предложил в 1949 г. М. Кенуй (это и есть "метод складного ножа") состоит в том, чтобы из одной выборки сделать много, исключая из нее по одному наблюдению (и возвращая ранее исключенные). Перечислим выборки, которые получаются из исходной:

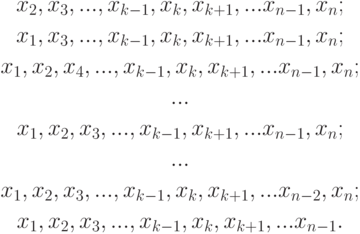
Всего новых (размноженных) выборок объемом 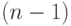каждая. По каждой из них можно рассчитать значение интересующей эконометрика статистики (с уменьшенным на 1 объемом выборки):

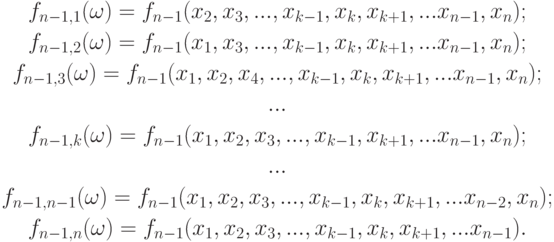
Полученные значения статистики позволяют судить о ее распределении и о характеристиках распределения - о математическом ожидании, медиане, квантилях, разбросе, среднем квадратическом отклонении. Значения статистики, построенные по размноженным подвыборкам, не являются независимыми. Однако, как мы видели в главе 9 на примере ряда статистик, возникающих в методе наименьших квадратов и в кластер-анализе (при обсуждении возможности объединения двух кластеров), при росте объема выборки влияние зависимости может ослабевать, а потому со значениями статистик типа 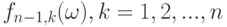можно обращаться как с независимыми случайными величинами.

Однако и без всякой вероятностно-статистической теории разброс величин 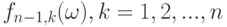дает наглядное представление о том, какую точность может дать рассматриваемая статистическая оценка.

Сам М. Кенуй и его последователи использовали размножение выборок в основном для построения оценок с уменьшенным смещением. А вот Б. Эфрон предложил новый способ размножения выборок, существенно использующий датчики псевдослучайных чисел. А именно, он предложил строить новые выборки, моделируя выборки из эмпирического распределения. Другими словами, Б. 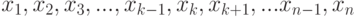Эфрон предложил взять конечную совокупность из элементов исходной выборки и с помощью датчика псевдослучайных чисел сформировать из нее любое число размноженных выборок. Процедура, хотя и нереальна без ЭВМ, проста с точки зрения программирования. По сравнению с описанной выше процедурой Кенуя появляются новые недостатки - неизбежные совпадения элементов размноженных выборок и зависимость от качества датчиков псевдослучайных чисел. Однако существует математическая теория, позволяющая (при некоторых предположениях и безграничном росте объема выборки) обосновать процедуры бутстрепа (см. сборник статей [ [ 13.49 ] ]).

Другой вариант построения размноженных выборок - более прямой. Исходные данные не могут быть определены совершенно точно и однозначно. Поэтому предлагается к исходным данным добавлять малые независимые одинаково распределенные погрешности. При таком подходе соединяем вместе идеи устойчивости и бутстрепа. При внимательном анализе многие идеи прикладной статистики тесно связаны друг с другом (см. статью [ [ 13.33 ] ]).

В каких случаях целесообразно применять бутстреп, а в каких - другие методы прикладной статистики? В период рекламной кампании встречались, в том числе в научно-популярных журналах, утверждения о том, что и для оценивания математического ожидания полезен бутстреп. Как показано в статье [ [ 13.33 ] ], это совершенно не так. При росте числа испытаний методом Монте-Карло бутстреп-оценка приближается к классической оценке - среднему арифметическому результатов наблюдений. Другими словами, бутстреп-оценка отличается от классической оценки только шумом псевдослучайных чисел.

Аналогичной является ситуация и в ряде других случаев. Там, где статистическая теория хорошо развита, где найдены методы анализа данных, в том или ином смысле близкие к оптимальным, бутстрепу делать нечего. А вот в новых областях со сложными алгоритмами, свойства которых недостаточно ясны, он представляет собой ценный инструмент для изучения ситуации.

Компьютерная статистика в контроллинге. В качестве примера применения компьютерной статистики рассмотрим конкретную прикладную область - контроллинг, т.е. современный подход к управлению организацией [ [ 13.18 ] ]. Контроллеру и сотрудничающему с ним статистику нужна разнообразная экономическая и управленческая информация, не менее нужны удобные инструменты ее анализа. Следовательно, информационная поддержка контроллинга необходима для успешной работы контроллера. Без современных компьютерных инструментов анализа и управления, основанных на продвинутых эконометрических и экономико-математических методах и моделях, невозможно эффективно принимать управленческие решения. Недаром специалисты по контроллингу большое внимание уделяют проблемам создания, развития и применения компьютерных систем поддержки принятия решений. Высокие статистические технологии и эконометрика - неотъемлемые части любой современной системы поддержки принятия экономических и управленческих решений.

Важная часть прикладной статистики - применение высоких статистических технологий к анализу конкретных экономических данных. Такие исследования зачастую требуют дополнительной теоретической работы по "доводке" статистических технологий применительно к конкретной ситуации. Большое значение для контроллинга имеют не только общие методы, но и конкретные эконометрические модели, например, вероятностно-статистические модели тех или иных процедур экспертных оценок или эконометрики качества, имитационные модели деятельности организации, прогнозирования в условиях риска. И конечно, такие конкретные применения, как расчет и прогнозирование индекса инфляции. Сейчас уже многим специалистам ясно, что годовой, квартальный или месячный бухгалтерский баланс предприятия может быть использован для оценки его финансово-хозяйственной деятельности только с привлечением данных об инфляции. Различные области экономической теории и практики в настоящее время еще далеко не согласованы. При оценке и сравнении инвестиционных проектов принято использовать такие характеристики, как чистая текущая стоимость, внутренняя норма доходности, основанные на введении в рассмотрение изменения стоимости денежной единицы во времени (это осуществляется с помощью дисконтирования). А вот при анализе финансово-хозяйственной деятельности организации на основе данных бухгалтерской отчетности изменение стоимости денежной единицы во времени по традиции не учитывают.

Специалисты по контроллингу должны быть вооружены современными средствами информационной поддержки, в том числе - на основе высоких статистических технологий и эконометрики. Очевидно, преподавание должно идти впереди практического применения. Ведь как применять то, чего не знаешь?

Статистические технологии применяют для анализа данных двух принципиально различных типов. Один из них - это результаты измерений (наблюдений, испытаний, анализов, опытов и др.) различных видов, например, результаты управленческого или бухгалтерского учета, данные статистической отчетности и др. Короче, речь идет об объективной информации. Другой - это оценки экспертов, на основе своего опыта и интуиции делающих заключения относительно экономических явлений и процессов. Очевидно, это - субъективная информация. В стабильной экономической ситуации, позволяющей рассматривать длинные временные ряды тех или иных экономических величин, полученных в сопоставимых условиях, данные первого типа вполне адекватны. В быстро меняющихся условиях приходится опираться на экспертные оценки. Такая новейшая часть прикладной статистики, как статистика нечисловых данных, была создана как ответ на запросы теории и практики экспертных оценок.

Для решения каких экономических задач может быть полезна прикладная статистика? Практически для всех, использующих конкретную информацию о реальном мире. Только чисто абстрактные, отвлеченные от реальности исследования могут обойтись без нее. В частности, прикладная статистика необходима для прогнозирования, в том числе поведения потребителей, а поэтому и для планирования. Выборочные исследования, в том числе выборочный контроль, основаны на прикладной статистике. Но планирование и контроль - основа контроллинга. Поэтому прикладная статистика - важная составляющая инструментария контроллера, воплощенного в компьютерной системе поддержки принятия решений, прежде всего оптимальных решений, которые предполагают опору на адекватные модели прикладной статистики. В производственном менеджменте это может означать, например, использование моделей экстремального планирования эксперимента (судя по накопленному опыту их практического использования, такие модели позволяют повысить выход полезного продукта на 30-300%).

Высокие статистические технологии предполагают адаптацию применяемых методов к меняющейся ситуации. Например, параметры прогностического индекса меняются вслед за изменением характеристик используемых для прогнозирования величин. Таков метод экспоненциального сглаживания. В соответствующем алгоритме расчетов значения временного ряда используются с весами. Веса уменьшаются по мере удаления в прошлое. Многие методы дискриминантного анализа основаны на применении обучающих выборок. Например, для построения рейтинга надежности банков можно с помощью экспертов составить две обучающие выборки - надежных и ненадежных банков. А затем с их помощью решать для вновь рассматриваемого банка, каков он - надежный или ненадежный, а также оценивать его надежность численно, т.е. вычислять значение рейтинга.

Один из способов построения адаптивных статистических моделей - нейронные сети (см., например, монографию [ [ 13.5 ] ]). При использовании нейронных сетей упор делается не на формулировку адаптивных алгоритмов анализа данных, а - в большинстве случаев - на построение виртуальной адаптивной структуры. Термин "виртуальная" означает, что "нейронная сеть" - это специализированная компьютерная программа, "нейроны" используются лишь при общении человека с компьютером. Методология нейронных сетей идет от идей кибернетики 1940-50-х годов. В компьютере создается модель мозга человека (весьма примитивная с точки зрения физиолога). Основа модели - весьма простые базовые элементы, называемые нейронами. Они соединены между собой так, что нейронные сети можно сравнить с хорошо знакомыми экономистам и инженерам блок-схемами. Каждый нейрон находится в одном из заданного множества состояний. Он получает импульсы от соседей по сети, изменяет свое состояние и сам рассылает импульсы. В результате состояние множества нейронов изменяется, что соответствует проведению статистических вычислений.

Нейроны обычно объединяются в слои (как правило, два-три). Среди них выделяются входной и выходной слои. Перед началом решения той или иной задачи производится настройка. Во-первых, устанавливаются связи между нейронами, соответствующие решаемой задаче. Во-вторых, проводится обучение, т.е. через нейронную сеть пропускаются обучающие выборки, для элементов которых требуемые результаты расчетов известны. Затем параметры сети модифицируются так, чтобы получить максимальное соответствие выходных значений заданным величинам.

С точки зрения точности расчетов (и оптимальности в том или ином статистическом смысле) нейронные сети не имеют преимуществ перед другими адаптивными системами прикладной статистики. Однако они более просты для восприятия. Надо отметить, что в прикладной статистике используются и модели, промежуточные между нейронными сетями и "обычными" системами регрессионных уравнений (одновременных и с лагами). Они тоже используют блок-схемы, как, например, универсальный метод моделирования связей социально-экономических факторов ЖОК (этот метод описан в "Статистика временных рядов" и [ [ 2.15 ] ]).

Профессионалу в области контроллинга полезны многочисленные интеллектуальные инструменты анализа данных, относящиеся к высоким статистическим технологиям и эконометрике. В частности, заметное место в математико-компьютерном обеспечении принятия решений в контроллинге занимают методы теории нечеткости.