|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Основы вероятностно-статистических методов описания неопределенностей
В дисперсионном анализе разработаны методы проверки подобных гипотез. Теория дисперсионного анализа и расчетные формулы рассмотрены в специальной литературе [ [ 2.6 ] ].
Гипотезу  проверяют против альтернативной гипотезы
проверяют против альтернативной гипотезы  , согласно которой хотя бы одно из указанных равенств не выполнено. Проверка этой гипотезы основана на следующем "разложении дисперсий", указанном Р.А.Фишером:
, согласно которой хотя бы одно из указанных равенств не выполнено. Проверка этой гипотезы основана на следующем "разложении дисперсий", указанном Р.А.Фишером:
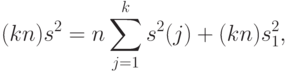 |
( 7) |
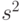 - выборочная дисперсия в объединенной выборке, т.е.
- выборочная дисперсия в объединенной выборке, т.е.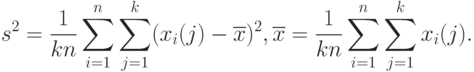
Далее, 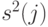 - выборочная дисперсия в
- выборочная дисперсия в  -ой группе,
s^2(j)=\frac{1}{n}\sum_{i=1}^n(x_i(j)-\overline{x}(j))^2,\overline{x}(j)=\frac{1}{n}\sum_{i=1}^n x_i(j),j=1,2,...,k.
-ой группе,
s^2(j)=\frac{1}{n}\sum_{i=1}^n(x_i(j)-\overline{x}(j))^2,\overline{x}(j)=\frac{1}{n}\sum_{i=1}^n x_i(j),j=1,2,...,k.
Таким образом, первое слагаемое в правой части формулы (7) отражает внутригрупповую дисперсию. Наконец, 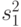 - межгрупповая дисперсия,
- межгрупповая дисперсия,
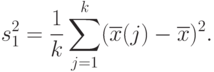
Область прикладной статистики, связанную с разложениями дисперсии типа формулы (7), называют дисперсионным анализом. В качестве примера задачи дисперсионного анализа рассмотрим проверку приведенной выше гипотезы  в предположении, что результаты измерений независимы и в каждой выборке имеют нормальное распределение
в предположении, что результаты измерений независимы и в каждой выборке имеют нормальное распределение 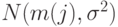 с одной и той же дисперсией. При справедливости
с одной и той же дисперсией. При справедливости  первое слагаемое в правой части формулы (7), деленное на
первое слагаемое в правой части формулы (7), деленное на  , имеет распределение хи-квадрат с
, имеет распределение хи-квадрат с 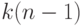 степенями свободы, а второе слагаемое, деленное на
степенями свободы, а второе слагаемое, деленное на  , также имеет распределение хи-квадрат, но с
, также имеет распределение хи-квадрат, но с  степенями свободы, причем первое и второе слагаемые независимы как случайные величины. Поэтому случайная величина
степенями свободы, причем первое и второе слагаемые независимы как случайные величины. Поэтому случайная величина
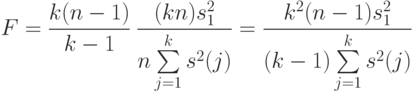
 степенями свободы числителя и
степенями свободы числителя и 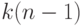 степенями свободы знаменателя. Гипотеза
степенями свободы знаменателя. Гипотеза  принимается, если
принимается, если 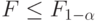 , и отвергается в противном случае, где
, и отвергается в противном случае, где 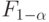 - квантиль порядка
- квантиль порядка 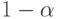 распределения Фишера с указанными числами степеней свободы. Такой выбор критической области определяется тем, что при
распределения Фишера с указанными числами степеней свободы. Такой выбор критической области определяется тем, что при  величина
величина  безгранично увеличивается при росте объема выборок
безгранично увеличивается при росте объема выборок  . Значения
. Значения 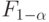 берут из соответствующих таблиц [
[
2.1
]
].
берут из соответствующих таблиц [
[
2.1
]
].Разработаны непараметрические методы решения классических задач дисперсионного анализа [
[
2.21
]
], в частности, проверки гипотезы  .
.
Следующий тип задач многомерного статистического анализа - задачи классификации. Они, согласно [ [ 2.6 ] , [ 2.16 ] ], делятся на три принципиально различных вида - дискриминантный анализ, кластер-анализ, задачи группировки.
Задача дискриминантного анализа состоит в нахождении правила отнесения наблюдаемого объекта к одному из ранее описанных классов. При этом объекты описывают в математической модели с помощью векторов, координаты которых - результаты наблюдения ряда признаков у каждого объекта. Классы описывают либо непосредственно в математических терминах, либо с помощью обучающих выборок. Обучающая выборка - это выборка, для каждого элемента которой указано, к какому классу он относится.
Рассмотрим пример применения дискриминантного анализа для принятия решений в технической диагностике. Пусть по результатам измерения ряда параметров продукции необходимо установить наличие или отсутствие дефектов. В этом случае для элементов обучающей выборки указаны дефекты, обнаруженные в ходе дополнительного исследования, например, проведенного после определенного периода эксплуатации. Дискриминантный анализ позволяет сократить объем контроля, а также предсказать будущее поведение продукции. Дискриминантный анализ сходен с регрессионным - первый позволяет предсказывать значение качественного признака, а второй - количественного. В статистике объектов нечисловой природы разработана математическая схема, частными случаями которой являются регрессионный и дискриминантный анализы [ [ 2.15 ] ].
Кластерный анализ применяют, когда по статистическим данным необходимо разделить элементы выборки на группы. Причем два элемента группы из одной и той же группы должны быть "близкими" по совокупности значений измеренных у них признаков, а два элемента из разных групп должны быть "далекими" в том же смысле. В отличие от дискриминантного в кластер-анализе классы не заданы, а формируются в процессе обработки статистических данных. Например, кластер-анализ может быть применен для разбиения совокупности марок стали (или марок холодильников) на группы сходных между собой.
Другой вид кластер-анализа - разбиение близких между собой признаков на группы. Показателем близости признаков может служить выборочный коэффициент корреляции. Цель кластер-анализа признаков может состоять в уменьшении числа контролируемых параметров, что позволяет существенно сократить затраты на контроль. Для этого из группы тесно связанных между собой признаков (у которых коэффициент корреляции близок к 1 - своему максимальному значению) измеряют значение одного, а значения остальных рассчитывают с помощью регрессионного анализа.
Задачи группировки решают тогда, когда классы заранее не заданы и не обязаны быть "далекими" друг от друга. Примером является группировка студентов по учебным группам. В технике решением задачи группировки часто является параметрический ряд - возможные типоразмеры группируются согласно элементам параметрического ряда. В литературе, нормативно-технических и инструктивно-методических документах по прикладной статистике также иногда используется группировка результатов наблюдений (например, при построении гистограмм).
Задачи классификации решают не только в многомерном статистическом анализе, но и тогда, когда результатами наблюдений являются числа, функции или объекты нечисловой природы. Так, многие алгоритмы кластер-анализа используют только расстояния между объектами. Поэтому их можно применять и для классификации объектов нечисловой природы, лишь бы были заданы расстояния между ними. Простейшая задача классификации такова: даны две независимые выборки, требуется определить, представляют они два класса или один. В одномерной статистике эта задача сводится к проверке гипотезы однородности [ [ 2.16 ] ].
Третий раздел многомерного статистического анализа - задачи снижения размерности (сжатия информации). Цель их решения состоит в определении набора производных показателей, полученных преобразованием исходных признаков, такого, что число производных показателей значительно меньше числа исходных признаков, но они содержат возможно большую часть информации, имеющейся в исходных статистических данных. Задачи снижения размерности решают с помощью методов многомерного шкалирования, главных компонент, факторного анализа и др. Например, в простейшей модели многомерного шкалирования исходные данные - попарные расстояния 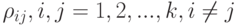 , между
, между  объектами, а цель расчетов состоит в представлении объектов точками на плоскости. Это дает возможность в буквальном смысле слова увидеть, как объекты соотносятся между собой.
Для достижения этой цели необходимо каждому объекту поставить в соответствие точку на плоскости так, чтобы попарные расстояния
объектами, а цель расчетов состоит в представлении объектов точками на плоскости. Это дает возможность в буквальном смысле слова увидеть, как объекты соотносятся между собой.
Для достижения этой цели необходимо каждому объекту поставить в соответствие точку на плоскости так, чтобы попарные расстояния 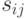 между точками, соответствующими объектам с номерами
между точками, соответствующими объектам с номерами  и
и  , возможно точнее воспроизводили расстояния
, возможно точнее воспроизводили расстояния 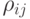 между этими объектами. Согласно основной идее метода наименьших квадратов находят точки на плоскости так, чтобы величина
между этими объектами. Согласно основной идее метода наименьших квадратов находят точки на плоскости так, чтобы величина
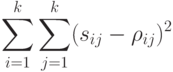
Статистика случайных процессов и временных рядов. Методы статистики случайных процессов и временных рядов применяют для постановки и решения, в частности, следующих задач:
- предсказание будущего развития случайного процесса или временного ряда;
- управление случайным процессом (временным рядом) с целью достижения поставленных целей, например, заданных значений контролируемых параметров;
- построение вероятностной модели реального процесса, обычно длящегося во времени, и изучение свойств этой модели.
Пример 1. При внедрении статистического регулирования технологического процесса необходимо проверить, что в налаженном состоянии математическое ожидание контролируемого параметра не меняется со временем. Если подобное изменение будет обнаружено, то необходимо установить подналадочное устройство.
Пример 2. Следящие системы, например, входящие в состав автоматизированной системы управления технологическим процессом, должны выделять полезный сигнал на фоне шумов. Это - задача оценивания (полезного сигнала), в то время как в примере 1 речь шла о задаче проверки гипотезы.
Методы статистики случайных процессов и временных рядов описаны в литературе [ [ 2.6 ] , [ 2.16 ] ].
Статистика объектов нечисловой природы. Методы статистики объектов нечисловой природы применяют всегда, когда результаты наблюдений являются объектами нечисловой природы. Например, сообщениями о годности или дефектности единиц продукции; информацией о сортности единиц продукции; разбиениями единиц продукции на группы соответственно значению контролируемых параметров; упорядочениями единиц продукции по качеству или инвестиционных проектов по предпочтительности; фотографиями поверхности изделия, пораженной коррозией, и т.д. Итак, объекты нечисловой природы - это измерения по качественному признаку, множества, бинарные отношения (разбиения, упорядочения и др.) и многие другие математические объекты [ [ 2.16 ] ]. Они используются в различных вероятностно-статистических методах принятия решений. В частности, в задачах управления качеством продукции, а также, например, в медицине и социологии, как для описания результатов приборных измерений, так и для анализа экспертных оценок.
Для описания данных, являющихся объектами нечисловой природы, применяют, в частности, таблицы сопряженности, а в качестве средних величин - решения оптимизационных задач [ [ 2.16 ] ]. В качестве выборочных средних для измерений в порядковой шкале используют медиану и моду, а в шкале наименований - только моду. О методах классификации нечисловых данных говорилось выше.
Для решения параметрических задач оценивания используют оптимизационный подход, метод одношаговых оценок, метод максимального правдоподобия, метод устойчивых оценок. Для решения непараметрических задач оценивания наряду с оптимизационными подходами к оцениванию характеристик используют непараметрические оценки распределения случайного элемента, плотности распределения, функции, выражающей зависимость [ [ 2.16 ] ].
В качестве примера методов проверки статистических гипотез для объектов нечисловой природы рассмотрим критерий "хи-квадрат" (обозначают 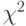 ), разработанный К.Пирсоном для проверки гипотезы однородности (другими словами, совпадения) распределений, соответствующих двум независимым выборкам.
), разработанный К.Пирсоном для проверки гипотезы однородности (другими словами, совпадения) распределений, соответствующих двум независимым выборкам.
Рассматриваются две выборки объемов  и
и 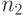 , состоящие из результатов наблюдений качественного признака, имеющего
, состоящие из результатов наблюдений качественного признака, имеющего  градаций. Пусть
градаций. Пусть 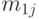 и
и 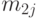 - количества элементов первой и второй выборок соответственно, для которых наблюдается
- количества элементов первой и второй выборок соответственно, для которых наблюдается  -я градация, а
-я градация, а 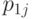 и
и 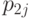 - вероятности того, что эта градация будет принята, для элементов первой и второй выборок,
- вероятности того, что эта градация будет принята, для элементов первой и второй выборок, 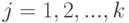 .
.
Для проверки гипотезы однородности распределений, соответствующих двум независимым выборкам,
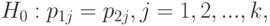
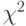 (хи-квадрат) со статистикой
(хи-квадрат) со статистикой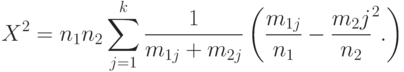
Установлено [  ,
, 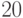 ], что статистика
], что статистика 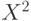 при больших объемах выборок
при больших объемах выборок  и
и 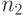 имеет асимптотическое распределение хи-квадрат с
имеет асимптотическое распределение хи-квадрат с  степенью свободы.
степенью свободы.
| Содержание серы, в % | Число плавок | |
|---|---|---|
| Завод А | Завод Б | |
0,00  0,02 0,02 |
82 | 63 |
0,02  0,04 0,04 |
535 | 429 |
0,04  0,06 0,06 |
1173 | 995 |
0,06  0,08 0,08 |
1714 | 1307 |
Пример 3. В табл.2.6 приведены данные о содержании серы в углеродистой стали, выплавляемой двумя металлургическими заводами. Проверим, можно ли считать распределения примеси серы в плавках стали этих двух заводов одинаковыми.
Расчет по данным табл.2.6 дает 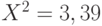 . Квантиль порядка 0,95 распределения хи-квадрат с
. Квантиль порядка 0,95 распределения хи-квадрат с 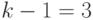 степенями свободы равна
степенями свободы равна 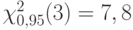 , а потому гипотезу о совпадении функций распределения содержания серы в плавках двух заводов нельзя отклонить, т.е. ее следует принять (на уровне значимости
, а потому гипотезу о совпадении функций распределения содержания серы в плавках двух заводов нельзя отклонить, т.е. ее следует принять (на уровне значимости 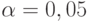 ).
).
Подробнее методы статистики объектов нечисловой природы рассмотрены в третьей части учебника.
Выше дано лишь краткое описание содержания прикладной статистики на современном этапе. Подробное изложение конкретных методов содержится в дальнейших лекциях учебника и в специальной литературе.
